Summer meeting 2014

York, June 11

13:30   Fionntan Roukema (Sheffield)   Knots with exceptional pairs at maximal distance

           

           

14:30   John Parker (Durham)   Non-arithmetic lattices

           

           

15:30   Coffee

16:00   Saul Schleimer (Warwick)   Algorithmic Topology

       

           

17:00   Marc Lackenby (Oxford)   Knottedness is in NP

           

           

19:00   Dinner  

Tying knots, and then trying to untie them, is far older than topology. Note that if a string has a loose end then, by doubling back and following along, any knot can theoretically be untied. However, as realized by Alexander the Great, when the two ends of the string are joined to form a loop the unknotting problem becomes more difficult!

Here is a mathematical phrasing: ``Can a given loop be continuously deformed, without self intersection, to be a round circle?''. Note how the requirement of continuity rules out Alexander's solution. We will discuss the computational complexity of the unknotting problem and other, closely related, problems in low-dimensional topology.

Timetable

The complement of a knot is usually hyperbolic. Moreover, when a solid torus is glued to the boundary of a hyperbolic knot, the result is also usually hyperbolic. In this talk we will give an overview of important results about hyperbolic manifolds and exceptional Dehn surgeries due to Thurston, Lackenby, and Meyerhoff. These results quantify what is meant above by ``usually". From there, we will look at a (possibly complete) list of ``exceptional" exceptions to the rule at ``maximal distance".

In a famous paper from 1980 Mostow constructed non-arithmetic lattices in PU(2,1), the holomorphic isometry group of complex hyperbolic 2-space. In 1986 Deligne and Mostow gave more examples, falling into 9 commensurability classes, together with a single non-arithmetic lattice in PU(3,1). No more examples were constructed until 2013 when Martin Deraux, Julien Paupert and I announced the construction of 5 more lattices. I will give a gentle survey of this problem and I will outline our new examples.

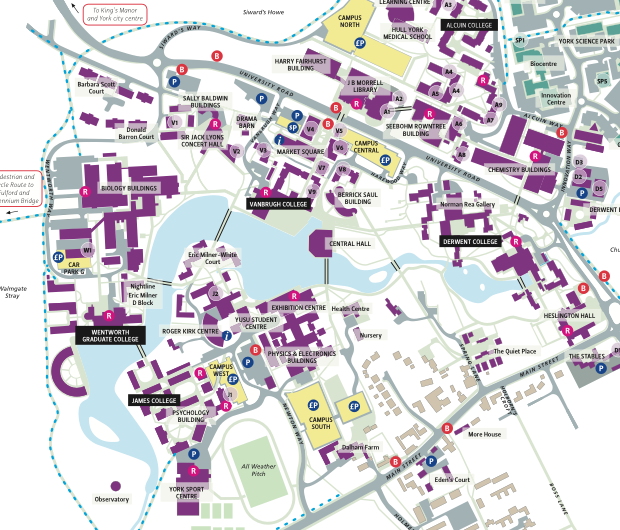
Getting here

Gather in the foyer of the Roger Kirk Centre for lunch (marked on the map below) from 12:30 onwards. The Maths department is next door. The talks are in room BB/103 in Biology (across the lake). The easiest way to find the room is to enter the Biology buildings where indicated by the arrow and then follow the signs to BB/103.

If you are coming by train catch either the number 4 bus (First) or the number 44 bus (UniBus) from outside the front of the station. Single fare is £1.50 and the journey takes approximately 15 minutes. Get off at the stop on University Road, marked on the map. You can tell the stop by the over-bridge that the bus stops under.  Warning: there is another bus, number 6 (First), that goes to the new Heslington East campus of the university. You don’t want this one.

If you are coming by car you can find more instructions on reaching the university here. The closest car parks to Roger Kirk and Maths are Campus West and Campus South. Parking is pay and display and costs £6 for the day (or £1 an hour).

More maps and information for visitors are here.

Given a knot diagram, can we efficiently decide whether it is the unknot? It is not known whether there is an algorithm that runs in polynomial time, as a function of the number of crossings. But it is a theorem of Hass, Lagarias and Pippenger that this decision problem lies in NP. In other words, if the knot is the unknot, then one can certify this in polynomial time. In my talk, I will explain why the complementary problem is also in NP: if the knot is knotted, then one may also certify this in polynomial time. This theorem was announced by Ian Agol in 2002, but he never gave full details of the proof. In 2011, Greg Kuperberg gave a proof, but he needed to assume the Generalised Riemann Hypothesis. In my talk, I will explain how a proof of the unconditional result can be built upon my earlier work on Dehn surgery.

(all talks are in BB/103)

CAR PARKS

ROGER KIRK

BB/103

MATHS

BUS STOP