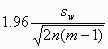
This note describes how to choose the sample size to estimate the within subject standard deviation, sw. This is described in a Statistics Note in the BMJ. We assume that the within-subject standard deviation is the same throughout the range, in order to estimate it. We also assume that within the subject the distribution of observations is Normal, to estimate the standard error. For the estimation of sample size, I shall consider only the case where there are equal numbers of observations on each subject, as I do not think one would plan an investigation with unequal numbers.
The precision with which we can estimate sw depends on both the number of subjects, n, and the number of observations per subject, m. The width of the 95% confidence interval for the population within-subject standard deviation is
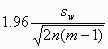
on either side of the estimate. (This is explained in another FAQ answer: "What is the standard error of the within-subject standard deviation, sw?".) A convenient way to deal with the dependence of the standard error, and hence the sample size, on the quantity we wish to estimate, is to think of estimating it to within some fraction of the population value, such as 10%. To find the sample size, we set
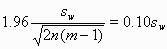
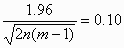
This is an equation with two unknown quantities, so there are many combinations of n and m which will give the required precision.
One solution would be to take all the observations on a single subject, i.e. to put n = 1. This is not an attractive idea, as some individuals may have more variation than others, and the variation may not be the same throughout the range of measurement. The standard error formula was derived under the assumptions of a simplistic model: that the variation is the same for everyone. This is quite adequate to enable us to estimate the mean variation, but we must collect the data allowing for the possibility that the data to not follow it exactly. We need several subjects with measurements covering the whole range in which we are interested.
Returning to the example, suppose we know that we can make repeated measurements on 20 subjects. How many measurements should we take on each? We put n = 20 and solve for m, giving
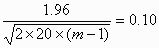
and so
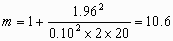
Hence m = 11, to the nearest integer, and we require 11 measurements on each of 20 subjects.
Alternatively, we may decide that there is an upper limit to the number of measurements per subject, perhaps because of the discomfort caused. If we can take only two measurements per subject, for example, we have m = 2 giving us
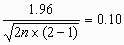
hence
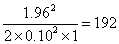
As so often happens in statistics, accuracy requires a large sample size.
We could set a less stringent target for accuracy. For example, we could set the confidence interval as 20% either side of the estimate of sw. For m = 2 observations per subject, we would require
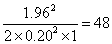
subjects.
I am very grateful to Garry Anderson for pointing out errors on this page.
Back to Frequently asked questions on the design and analysis of measurement studies .
Back to measurement studies menu.
Back to Martin Bland's Home Page.
This page maintained by Martin Bland.
Last updated: 17 May, 2010.