During the discussion session of this Conference the question was once again raised concerning the appropriateness of the transactional interpretation's use of advanced waves in the interpretation of quantum formalisms which do not have advanced solutions. This question was carefully addressed in my RMP article, but since the issue has been raised, let me address it here.
The wave equation which has been the focus of most of the discussion surrounding the interpretation of quantum mechanics is the Schrödinger equation:
where m is the mass of the particle described by the equation. This equation
is first order in the time variable and for this reason does not have advanced
solutions. Therefore, if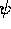 
=F(r,t) is a solution of the Schrödinger
equation, then 
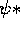=G(r,t) is not a solution, nor is a linear combination of F
and G as used in the transactional model.
We must bear in mind, however, that the Schrödinger equation is ultimately not physically correct because it is not relativistically invariant. It should properly be considered as the limiting case, in a restricted non-relativistic domain, of some more physically reasonable relativistically invariant wave equation, e.g., the Dirac equation or the Klein-Gordon equation. These relativistic equations, like the electromagnetic wave equation, have both advanced and retarded solutions.
Considering the Schrödinger equation as a limiting case, the apparent problem created by its lack of advanced solutions can be resolved. When a suitable relativistic wave equations is reduced to the Schrödinger equation by taking a non-relativistic limit[5], the reduction procedure leads to two distinct equations, the Schrödinger equation and another equation of the form:
which is the complex conjugate or time reverse of the Schrödinger equation.
This equation has only advanced solutions. Equations (1) and (2) are equally
valid non-relativistic reductions of relativistic dynamics, but equation (2)
is usually dropped because it has negative energy eigenvalues. From this it
should be clear that F(r,t) and G(r,t) (or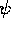 
and 
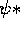) are equally valid
solutions of the dynamics which underlies the Schrödinger equation. It is
therefore valid to use advanced solutions in the transactional model in the
non-relativistic limit as if they were solutions of the Schrödinger
equation.
We can also look at the need for relativistic invariance in another way. The interpretational problem of nonlocality, as mentioned above, is essentially a relativistic problem. If the velocity of light were infinite the locality problem would not exist: there would be no difference between local and non-local descriptions. The Schrödinger equation can be considered as the limiting case of a relativistically invariant wave equation when the velocity of light goes to infinity. Therefore it is not particularly surprising that an explicitly non-local description such as the transactional model may have intrinsic inconsistencies with the Schrödinger equation and may require certain properties of relativistically invariant wave equations. This is a subtle link between relativity and quantum mechanics which has not, perhaps, been previously appreciated.
However, let it be clearly understood that the transactional interpretation of quantum mechanics is applicable only to quantum mechanical formalisms that either have advanced solutions or that are special cases or reductions of more general formalisms that have advanced solutions. It is my view that valid QM formalisms that do not satisfy this criterion are a null set, but this proposition has not been proved.
