Experiment AP2

Approximate Duration: 1 Term

The Height of Lunar Features

Download the full PDF laboratory script.

Safety Hazards and Precautions

Please note that the following precautions apply to all observing sessions in the optical observatory:

• The observatory door must be locked to prevent intruder access during observing sessions.
• Care should be taken in the dark in the observatory that wires are not placed in a hazardous position and that backpacks, books or other accessories do not become trip hazards.
• Students should work in pairs in the observatory and ensure that dress is appropriate for cold night observing.
• All observatory rules must be obeyed for safety reasons and usage taught in training adopted.

Experimental objectives

• To measure the height of lunar surface features by measuring the lengths of shadows.
• To compare results with accepted values.

Learning objectives

• To gain experience with the Departmental Telescope to make visual observations.
• To learn how to record astronomical images using the CCD camera.
• To learn how to use image processing programs to enhance and analyse CCD images.
• To learn how to analyse lunar astronomical images in order to obtain data on the properties of lunar features.

Introduction

On Earth the heights of surface features, e.g. mountains, can be quoted from a common datum, namely mean sea level. Since there is no such readily available surface on the moon it is only possible to quote the heights of features such as mountains or crater walls above the surrounding lunar surface.

There are a number of simple visual ways of determining the approximate height of lunar features. This one depends on measuring the length of shadows cast by the walls of the crater.

Galileo Galilee was the first person to perform similar measurements after using his simple telescope to observe the Moon. NASA and the US Air Force made measurements of this sort as part of the Apollo missions to the moon. These surveys were typically preformed from lunar orbiting satellites that took high-resolution pictures of the lunar surface. However, with some minor modifications, the same techniques can be used for ground-based observations.

Recently, interest has been rising regarding extra-planetary landings with the arrival at Mars of the EU Mars Landing Vehicle, the Beagle II, and the images obtained by the two NASA Landers, Spirit and Opportunity. The United States has also recently re-expressed interest in returning to the Moon with the calling for an "extended human presence" with the goal of "living and working there for increasing periods of time" as part of a vision to bring people to the surface of Mars.

In this laboratory, you will take photographs of the Moon with the CCD camera and the telescope in the Department of Physics. These images will enable you to measure the heights of the various lunar features around the Apollo 15 lunar landing site. If you are not able to obtain your own photographs, additional images will be provided for your analysis.

Procedure and Objectives

Here, the procedure and objectives are determined by whether you have been able to perform any observations of the moon and successfully obtained any CCD images.

1. If you have taken CCD images of the moon:
   
   a) If you have obtained CCD images of the moon using the telescope in the department on 2 or more different days that are close to each other, you should choose any 3 features with useful shadows on at least 2 different days and determine the heights, with estimates of the error, according to the general procedure. If possible, these features should be around the Apollo 15 landing site.
   
   b) If you have obtained CCD images of the moon using the telescope in the department on only 1 evening, then you should choose any 6 features with useful shadows and determine the heights, with estimates of the errors, according to the general procedure. If possible, these features should be around the Apollo 15 landing site.
   
2. If you have obtained no CCD images of the moon:
   
   a) You will use the archived CCD images of the moon taken by Earth-based observatories from the MicroObservatory Online Telescope Archive to determine the heights of 6 different features in the vicinity of the Apollo 15 landing site. These archived images contain the full disk of the moon and are low-resolution images. You will follow the general procedure for Earth-based observations of the moon. The images are in the folder MicroObservatory_Archive.
   
   b) You will use the archived CCD images of the moon taken by 61" Earth-based NASA Telescope at the Catalina Observatory to determine the heights of 6 different features, including Mons Hadley, on the two different days (in order to estimate the uncertainty) in the vicinity of the Apollo 15 landing site. These archived images are high-resolution images but do not contain the full disk or limb of the moon. You will follow the general procedure for Earth-based observations of the moon for this case. The images are in the folder NASA_Archive.
   
   c) You will use the archived CCD images of the moon taken by the Lunar Orbiter program of the Apollo 15 landing site to determine the heights of the same 6 lunar features from part 2) b., above. These are high-resolution images of the lunar surface taken from orbiting NASA satellites. You will follow the general procedure for the Orbiter-based observations of the moon. The images are in the folder Lunar_Orbiter_Archive.

Part A: Earth-based Observations of the Moon

(For the analysis of either archived images or the lunar images obtained at York)

1. Acquire Image(s) of Lunar Mountains
   
   You will investigate the height of the lunar features in the vicinity of the Apollo 15 lunar landing site. The Apollo 15 lunar module, the Falcon, landed on the surface near the Apennine Mountains on July 30 1971. The Falcon was the first Lander to carry a Moon Rover that was used by Astronauts David Scott and James Irwin to explore the lunar landscape.
   
   
2. Configure Virtual Moon Atlas
   
   It may only be possible to run Virtual Moon Atlas Light from your computer. If this is the case, start the program from the Start/Programs/Virtual Moon Atlas/ and choose Virtual Moon Atlas Light. Virtual Moon Atlas is a program that is very useful for helping you to study the Moon. You must, when you run the program, ensure that the Latitude and Longitude in the configuration option reflects your observatory location. You can the set the time and date in the Ephemeris bar to obtain additional useful information.
   
   Use the program Virtual Moon Atlas or other lunar charts (e.g. Norton's Star Atlas or using a lunar map on the web such as at http://www.lpi.usra.edu/research/lunar_orbiter/) to identify the Apollo 15 landing site. Determine the identity and location of some features near this landing site. You will determine the height of those features from the shadows that are cast on the lunar surface. Determine the moon phase that would enable these features to have long shadows. Bear in mind the fact that you will need long shadows from the lunar feature to make accurate measurements. Consequently, it is best to select these features when they are near the terminator. Decide whether the features will be visible at the first or third quarter.
   
   
3. Obtaining Images
   
   a) Using your own CCD Images of the Moon
   
   Photograph the features on the nights you determine are best, If the observing conditions prevent observation at these times then find other times when the sky is clear, but not near full moon since the shadows will be short or non-existent. You will probably need to take several exposures with different exposure times and choose the best images. Make sure to save the Moon images in FITS file format. On any observing sessions you will need to take at least one image that would contain the curvature of the disk of the moon. This will enable you to determine the resolution of your image in pixels/km.
   
   Remember that you will need to analyse more than one final image in order to get an idea of the uncertainty in your results. Hence you need to take advantage of several available clear evenings to get your images. Plan ahead by checking when the Moon will be visible using the prediction software in the observatory, or an astronomical almanac, or the program ICE.
   
   b) Using Archived CCD images of the Moon
   
   1. Archived images of the Moon obtained recently have been saved for your use. The images were obtained using the MicroObservatory Online Telescopes at http://mo-www.harvard.edu/MicroObservatory/ and contain the full disk of the moon in each image. The telescopes were developed at the Harvard-Smithsonian Center for Astrophysics in the United States and were designed to enable people to use telescopes remotely and for educational purposes. The Moon images have filenames designated by UT, such as Moon010204002911.FITS, and are stored on your computer in the directory C:\LAB\ MicroObservatory_Archive\. The file name time stamp will differ from the local time of the photograph. Obtain the Moon photographs for the times you determine are best to study the features near the Apollo 15 landing site. If the observing conditions prevent observation at these times then the files will be missing or blank. You must choose other times, when the sky is clear at the observatory used by the MicroObservatory, but not near full moon since the shadows will be short or non-existent.
   
   2. Two archived images containing the Apollo 15 landing area have been taken from the 61" Earth-based NASA Telescope at the Catalina Observatory. These archived images are high-resolution images but do not contain the full disk or limb of the moon. The images are in the folder NASA_Archive and you must use Image/J to analyse them since the files at in JPG format. You will use both photographs because they were taken on different days with different solar colatitudes and thus have different shadow lengths. You will use both images in order to estimate the uncertainties of the heights of the same features. Information on each image follows:
   
   C10.jpg
   Date: 1966 May 28d 04h 6.2m UT
   Colongitude 10.1 deg

   C9.jpg
   Date: 1967 Jan 1d 03h 3.5m UT
   Colongitude: 7.2 deg
   
4. Determine the Selenographic Location of Mountains
   
   You must determine the lunar latitude and longitude of the lunar features in your image. Use the Virtual Moon Atlas to obtain the latitude and longitude of your lunar feature. Use the convention that western longitudes are positive, and eastern longitudes are negative.
   
   If you can find the names for your lunar features, record them. You may be able to look up more information about the features in the Virtual Moon Atlas and other lunar resources.
   
   
5. Measure Apparent Length of Shadows
   
   Using any image-processing program, such as Image/J, ds9 or fv (which are all described below) to open the FITS image of the Moon. Use the program to measure the number of pixels from the peak of the feature to the end of the shadow it casts. You may find that it is easiest to rotate, enhance, zoom-in, or otherwise process your image in order to assist with this measurement. It is also easy to place a line on your image and measure the distance in pixels or analyse the line by projecting out the profile. You should also read the FITS file header or otherwise obtain important information about your image from the FITS file, such as the time and date of the photograph and Longitude and Latitude of the observatory.
   
   For example, pick several craters in the image with sharp, well-defined rims or walls. Measure and record the size of these craters in their longest dimension.
   
   
6. Measure the Resolution of your Image
   
   Each pixel in the image will correspond to a distance on the lunar surface. You must determine this scale and therefore the resolution.
   
   
   A) Full Disk Image: If your image of the moon contains the whole disk, such as shown in Figure 1, then you can draw a diameter as illustrated and determine the length of the diameter in pixels. Since the diameter of the moon is known, you can then find out the resolution in km/pixel.
   
   

   
   B) Limb Image: If you have an image of the moon showing just a limb, you need to draw a line from one edge of the limb to another. This is illustrated in Figure 2. The line that you have drawn is the Chord, L. Measure the Chord. From the midpoint draw the segment, d, which is perpendicular to the chord, from the chord to the limb of the Moon. The following equation can be easily derived. Derive this in your lab book.
   
   
   From this equation, the pixel resolution can be obtained in km/pixel.
   
   
   C) Image of Only the Lunar Features: If you have an image of the moon showing just a variety of lunar features (and without an example of the lunar limb in images taken at nearly the same time) it is a bit more complicated to determine your pixel resolution. It can be determined, though, by recognizing two different lunar features and measuring the distance between them in pixels and also deriving the distance between them in kilometres. The first requirement is accomplished by measuring the distance between the centres of each lunar feature in pixels. This is illustrated in Figure 3. The second requirement is obtained from the latitude and longitude of each lunar feature and calculating the distance between them as projected from a sphere onto the disk observed from the Earth. Effectively, you must convert from spherical coordinates to rectangular coordinates. This is illustrated in Figure 4. You must convert the position of each feature from the latitude and longitude on a sphere into Z and Y coordinates on the projected disk. The X-axis in the rectangular coordinate system will coincide with 0 degrees longitude and will also coincide with the axis of view from the earth. This is not absolutely correct, since there is a sub-earth latitude and longitude that varies with time and should be considered, but this effect will be small and will be ignored. It is also true that the moon is not quite spherical, but again this effect is small. The transformation equations are shown below.
   
   
   
   
   
   
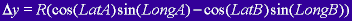
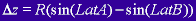
   The equations show the relationship between the radius of the moon, R, and the latitude and longitude of two recognisable features labelled A and B, (LatA and LongB, for example), to calculate the linear distance, D, between the two features in the YZ Plane. You can easily derive the equations using trigonometry. In the equations, is the projected difference along the Y-axis between the two features and is the projected difference along the Z-axis. The final distance, D, is what will be used with the pixel distance measurement in order to obtain the resolution in km/pixel.
   

   Now check your result: look in your image to find a few craters with sharp, well-defined rims or walls. Look up the names of these craters using the Virtual Moon Atlas. The program may also provide a diameter for some of these craters. If it does, measure the diameter of the crater and use your resolution factor to convert from pixels to kilometres. Does your measurement agree with the accepted value?
   
   If your image covers an area near the centre of the lunar disk then you should find an agreement between your measurement and the accepted value. But if your image shows an area far from the middle of the disk, then you will have neglected the fact that the lunar surface is not perpendicular to the camera. In that case, you will have to make a correction to the resolution based on angular size of a pixel, which ought to help you measure the proper sizes of craters.
   
   
7. Determine the Tilt of the Lunar Surface Relative to the Camera
   
   A picture of the centre of the lunar disk (near the lunar equator, halfway between the eastern and western limbs) has little or no distortion because the lunar surface is roughly face-on to the camera. But a picture of any other area will be tilted with respect to the camera; the closer the area is to the limb of the moon, the larger the tilt. This tilt causes foreshortening: it makes shadows appear to be shorter than they truly are. In the figure below, the true length, L, of the shadow appears to be shorter, L', when viewed from Earth. You will need to correct for this foreshortening.
   
   
   Use the lunar latitude and longitude of your lunar feature in the following formula:
   
   
   The correction factor is always larger than or equal to 1. Multiply your shadow length (in km) by this factor, and record the factor and the corrected shadow length (also in km).
   
   Check your results. Use this same factor to correct the measured diameters of craters in your image; compare to the known diameters of the craters (listed in the Virtual Moon Atlas). How close are your measurements to the accepted diameters?
   
   Note that this correction factor assumes that the observer is directly above the center of the lunar disk (so above latitude = 0, longitude = 0). However, the sub-earth point is usually a few degrees away. You would need to record the selenographic latitude and longitude of the sub-earth point, and then correctly calculate the correction factor. The sub-earth point latitude and longitude are the points in the centre of the projected lunar disk for observations from the Earth. However, including the effect from using the sub-earth latitude and longitude is usually very small and will be ignored for these calculations.
   
   
8. Determine the Altitude of the Sun over the Features at the time of the Image
   
   You need to know the altitude of the Sun above the lunar horizon at the time of the photograph in order to determine the mountain's height from the length of its shadow. You will need to obtain the following;
   
   Co: Colongitude of the Sun
   Bo: Subsolar point Lat
   
   Run the program, ICE, in order to obtain the subsolar point latitude, Bo, which is the latitude where the Sun's ray is vertical to the surface of the Moon. You will need to enter the initial values for the observatory longitude and latitude and the time the image was taken. Then you will need to run the program in order to calculate the Physical Ephemeris of the Moon for rotation. Record the subsolar and sub-earth latitude and longitude for the image.
   
   You will then need the Colongitude of the Sun. This is the longitude of the terminator on the day and time of the observation. You can obtain this information from running Virtual Moon Atlas and getting the information from the Ephemeris. Note that the Colongitude of the Sun on the Moon should be between 90 degrees West (+90) and 90 degrees East (-90 or 270) as seen from the vantage point of the Earth, so please convert the angle to be between 0 and +/- 90.
   
   You can now calculate the angle of the Sun above your lunar feature.
   
   
   For any feature which casts a long shadow, the angle should be between zero and fifteen degrees.
   
   
9. Calculate the Height of the Lunar Feature

   
   Consider the diagram in Figure 6:
   

   You know the length of the shadow, L, and the angle,. You can calculate the height of the lunar peak with simple trigonometry. Derive the formula you need to use, and calculate the height of the lunar features near the Apollo 15 landing site. What heights do you derive?
   
   How does this height compare to the height of mountains here on Earth? For example, Winslow Crater, Arizona, has crater wall heights of about 100m. Explain your measurements compared with this measurement.
   

Part B: Lunar Orbiter Program Image Analysis

(For use with archived images only.)

NASA needed to survey the surface of the Moon in the 1960s around the proposed landing sites for the Apollo missions. The Lunar Orbiter program launched five spacecraft into lunar orbit between 1966 and 1967 in order to complete this mission. These spacecraft photographed landing sites and areas of high scientific interest with medium-resolution cameras. You will survey these images of the landing site of the Apollo 15 mission in order to determine the heights of various lunar features and the distances between these features and the Apollo 15 landing site. Use the image from the 1994 Clementine Orbiter at the end of this script to have a better visual image of the Apollo 15 lunar landing site.

The archived images from the Lunar Orbiter program are in JPG format and are stored on your computer at C:\LAB\LunarOrbiterArchive. Therefore, you will need to use Image/J in order to analyse the photographs. Note that the photographs have already been enhanced and are of better final quality than many of the original photographs from the 1960s.

There are three photographs available for analysis. Each photograph also has an accompanying photograph with various lunar features identified. This file is named "iv_102_h3_labels.jpg", for example.

Information about each image and the lunar features identified within the scope of each image follows. Note that the sun angle is measured from the normal to the surface at the lunar feature.

• Sun Angle: 68.40 °
• Spacecraft Altitude: 2699.13 km
• Medium Res. Photo Center Coordinates: 12.96°N/3.63°E

Feature Name	Feature Latitude/Longitude	Feature Size
Apollo 15	26.1°N/3.7°E	km
Aratus	23.6°N/4.5°E	10 km
Conon	21.6°N/2.0°E	21 km
Galen	21.9°N/5.0°E	10 km
Joy	25.0°N/6.6°E	5 km
Mons Bradley	22.0°N/1.0°E	30 km
Mons Hadley	26.5°N/4.7°E	25 km
Mons Hadley Delta	25.8°N/3.8°E	15 km
Montes Apenninus	18.9°N/3.7°W	401 km
Palus Putredinis	26.5°N/0.4°E	161 km
Promontorium Fresnel	29.0°N/4.7°E	20 km
Rima Bradley	23.8°N/1.2°W	161 km
Rima Hadley	25.0°N/3.0°E	80 km
Santos-Dumont	27.7°N/4.8°E	8 km

IV_103_H1.JPG

• Sun Angle: 67.70 °
• Spacecraft Altitude: 2926.55 km
• Medium Res. Photo Center Coordinates: 41.82°N/11.28°E
  

• Sun Angle: 69.20 °
• Spacecraft Altitude: 2915.82 km
• Medium Res. Photo Center Coordinates: 42.59°N/3.35°E
  

You will need to determine the pixel resolution in a different way than proposed above for Earth-based observations. It can be determined, though, by recognizing two different lunar features and measuring the distance between them in pixels and also deriving the distance between them in kilometres. The first requirement is accomplished by measuring the distance between the centres of each lunar feature in pixels as illustrated earlier in Figure 3. The second requirement is obtained from the latitude and longitude of each lunar feature and calculating the distance between them

The easiest way to calculate the distance between two points in the photograph is to determine the linear distance between the two points using spherical coordinates. You can refer to Figure 4 for an illustration of some of this conversion. The following equations show the relationship between the radius of the moon, R, and the latitude and longitude of two recognisable features labelled A and B, (LatA and LongB, for example), to calculate the linear distance, D, between the two features. You can easily derive the following equations using trigonometry. In the following equations, is the projected difference along the x axis between the two features, while and are similar distance differences along the y and z axis. The final distance, D, is what will be used with the pixel distance measurement in order to obtain the resolution in km/pixel.

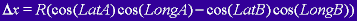
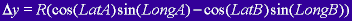
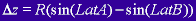
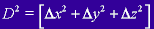
Use these relationships to determine the resolution of the photograph in km/pixel. Will you need to determine a correction factor to correct for foreshortening of the shadow length as you did earlier?

Derive an equation to determine the height of the lunar feature from the angle of the sun and the length of the shadow cast by the feature of interest. From this determine the height of the lunar feature.

Again, look for a number of good lunar features with well-defined shadows. You should attempt to identify and measure 6 such features for this exercise, including Mons Hadley. Also, determine the distance from the Apollo 15 landing site to the feature. A close-up of the Apollo 15 landing site was obtained by the Clementine Orbiter in 1994 and is included at the end of this script.

Example Results

The following are a set of heights that have been calculated using image C10 (from Part A) and IV_102_H3 (from Part B). You will see that only the heights calculated have been quoted alongside the heights given in Virtual Moon Atlas. The resolutions of the pictures will have to be worked out for yourselves, as well as the corresponding lengths of the shadows.

Image: C10.jpg

Click the thumbnail below to download C10.jpg (File Size: 960Kb)

Image: IV_102_H3.jpg

Click the thumbnail below to download IV_102_H3.jg

Do not forget to include an analysis of errors when carrying out these calculations! Errors have deliberately not been quoted here so as to not give you an indication of what are acceptable estimates for the heights of the features. It is up to you to decide on what is an acceptable result and what isn't. Are the above results acceptable? Where do you think the main sources of error will lie?

Software and Information:

1. Virtual Moon Atlas: This software by Patrick Chevalley and Christian Legrand shows the Moon and identifies various lunar features for an input date, time, and viewing coordinate on Earth. It has an excellent lunar formation library and an impressive picture library. You can download the software (as well as more expert versions of the Virtual Moon Atlas) for free from the web site at: http://www.astrosurf.com/avl/UK_index.html.
   
2. FITS files: FITS stands for Flexible Image Transport System and is the standard data interchange and archival format of the worldwide astronomy community. FITS preserves the spectroscopic information recorded in bits by the pixels of CCD cameras. A FITS file will also have a header before the binary image data that contains important information about image including the camera settings, exposure time, and location of the camera. The CCD camera in the Department Observatory will save images in this format or in TIF format. TIF does not preserve all the information in the image recorded by the CCD camera and makes analysis more difficult for certain systems.
   
3. Image/J and NIH Image: This is a public domain image processing and analysis program. It was developed at the Research Services Branch (RSB) of the National Institute of Mental Health (NIMH), part of the National Institutes of Health (NIH) This version is Image/J, a Java program that "runs anywhere" and can be obtained at http://rsb.info.nih.gov/ij/. This program can acquire, display, edit, enhance, analyse and animate images. It reads and writes FITS, TIFF, PICT, PICS and MacPaint files, providing compatibility with many other applications, including programs for scanning, processing, editing, publishing and analysing images. It supports many standard image processing functions, including contrast enhancement, density profiling, smoothing, sharpening, edge detection, median filtering, and spatial convolution with user defined kernels. It can be used to measure area, mean, centroid, perimeter, etc. of user defined regions of interest. It also performs automated particle analysis and provides tools for measuring path lengths and angles. Spatial calibration is supported to provide real world area and length measurements. Density calibration can be done against radiation or optical density standards using user specified units. Results can be printed, exported to text files, or copied to the Clipboard. A tool palette supports editing of colour and grey scale images, including the ability to draw lines, rectangles and text. It can flip, rotate, invert and scale selections. It supports multiple windows and 8 levels of magnification. All editing, filtering, and measurement functions operate at any level of magnification and are undoable.
   
4. ds9: This software is an image display program that can read, display, enhance, and analyse FITS files. The ds9 program was developed at Harvard University to view data obtained by the Chandra X-ray Observatory. The Chandra homepage, where the program can be found and freely downloaded and where you can access Chandra data for viewing and analysis can be found at http://chandra-ed.harvard.edu/index.html. Please note that some FITS images have headers that cannot be read by this software.
   
5. fv: This software is an interactive FITS file editor and viewer from NASA, available from http://heasarc.gsfc.nasa.gov/docs/software/ftools/fv/. Version 4.1 became available on 20 January 2004. It is a powerful and general-purpose FITS file editor (formerly just a file viewer) able to manipulate virtually all aspects of a FITS file and perform basic data analysis of its contents.
   
6. ICE: Interactive Computer Ephemeris is a program developed by the U.S. Naval Observatory to calculate the positions, rise times, and set times of various solar system bodies. It is useful for the Physical Ephemeris calculations of the moon and can be downloaded for free from http://www.seds.org/billa/ice/ice.html.
   

Script Updated by Dr C J Barton (3rd Feb 2004)