North British Geometric Group Theory
Summer
meeting on Buildings
York,
May 27 2015
Timetable
(all talks are in Biology BB/002)
o
1230 Alina
Vdovina (Newcastle) Lattices, superrigidity and surfaces
One
of the most well known open questions in geometric group theory is the
following question of Gromov: is it true, that every
one-ended hyperbolic group contains a surfaces group? Even if we restrict
ourselves to groups acting on hyperbolic buildings the answer is not known in
general. We'll present some non-obvious embeddings of
surfaces groups into groups acting on buildings as well as some negative
results, leaving a possibility for counter-examples.
o
1330 Ben Martin
(Aberdeen) Spherical buildings and the
Centre Conjecture
The Centre Conjecture of Tits is a fixed-point theorem for certain subcomplexes of a spherical building. It was proved in a
series of papers by Muehlherr-Tits, Leeb-Ramos-Cuevas and Ramos-Cuevas. I will discuss
different approaches to this result via building theory, CAT(1)
metric spaces and algebraic groups. I will also describe a natural
generalisation of the Centre Conjecture which is motivated
by ideas from geometric invariant theory.
o
1430 Jeroen Schillewaert (Muenster) Projective embeddings of spherical buildings
I will discuss an ongoing project with H. Van Maldeghem concerning (exceptional) algebraic groups and
their associated geometries, one of our motives being to obtain a geometric
construction of the 248-dimensional E8-module.
The main goal is to give a uniform axiomatic description of the embeddings in projective space of the varieties
corresponding with the geometries of exceptional Lie type over arbitrary
fields. This comprises a purely geometric characterization of F4, E6, E7
and E8.
o
1530 Coffee
o
1600 Anne Thomas (Glasgow)
Affine Deligne-Lusztig
varieties and the geometry of Euclidean buildings
Let G be a reductive group
such as SLn
over the field k((t)), where k is an algebraic closure of a finite field, and let W be the affine Weyl group of G.
The associated affine Deligne-Lusztig
varieties Xx(b) were introduced by Rapoport. These are indexed by elements x in W
and b in G, and are related to many important concepts in algebraic geometry
over fields of positive characteristic. Basic questions about the
varieties Xx(b) which have remained
largely open include when they are nonempty, and if nonempty, their dimension.
We use techniques inspired by geometric group theory and representation
theory to address these questions in the case that b is a translation in W.
Our approach is constructive and type-free, sheds new light on the reasons for
existing results and conjectures, and reveals new patterns. Since we work
only in the standard apartment of the Euclidean building for G, which is just the tessellation of
Euclidean space induced by the action of the reflection group W, our results also hold over the p-adics. This
is joint work with Elizabeth Milicevic (Haverford)
and Petra Schwer (Karlsruhe).
o
1700 Bernhard
Muehlherr (Giessen) Moufang Trees
The Moufang condition was
introduced by Tits to characterize spherical buildings of algebraic origin. In
this context the rank 2 case is of particular
interest, because one knows that all spherical buildings of higher rank are
automatically Moufang. In the non-spherical case, Kac-Moody groups provide examples of group actions on buildings which naturally generalize the Moufang
condition.
Moufang
trees are precisely the non-spherical Moufang
buildings of rank 2 and represent a most interesting class. By work of Tits one
knows that the Moufang condition is not enough to
characterize those of algebraic origin (i.e the Bruhat-Tits trees). But it is an open question whether on
can classify these objects.
In my talk I will present the basic theory of Moufang trees. I will then present two recent results on Moufang trees. The first is a structure theorem for binary Moufang trees. The second is a classification of Moufang triple trees which
provides a characterization of certain arithmetic groups.
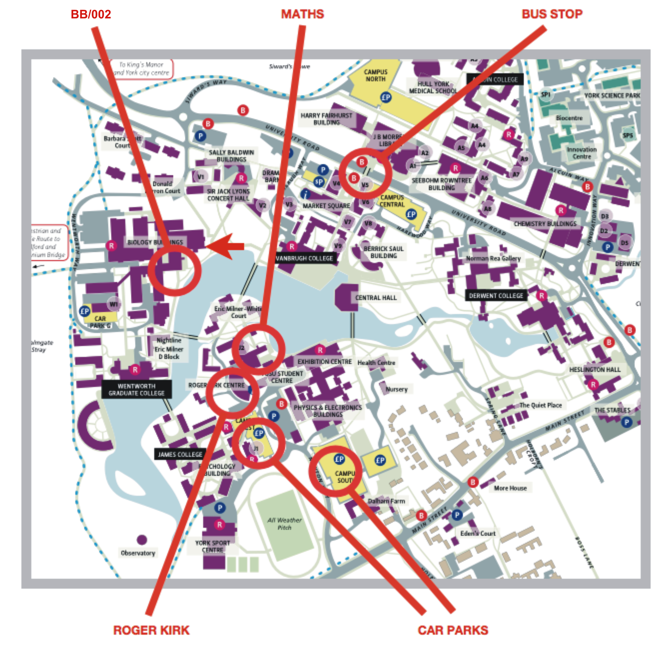
Getting here
Gather in the foyer of the Roger Kirk
Centre for lunch (marked on the map below) from 11:30 onwards. The Maths
department is next door. The talks are in room BB/002 in Biology (across the
lake). The easiest way to find the room is to enter the Biology buildings where
indicated by the arrow and then follow the signs to BB/002.
If you are coming by train catch
either the number 4 bus (First) or the number 44 bus (UniBus)
from outside the front of the station. Single fare is £1.50 and the journey
takes approximately 15 minutes. Get off at the stop on University Road, marked
on the map. You can tell the stop by the over-bridge that the bus stops under. Warning: there is another bus, number 6 (First), that goes to the new Heslington
East campus of the university. You donÕt want this one.
If you are coming by car you
can find more instructions on reaching the university here. The
closest car parks to Roger Kirk and Maths are Campus West and Campus South.
Parking is pay and display and costs £6 for the day (or £1 an hour).