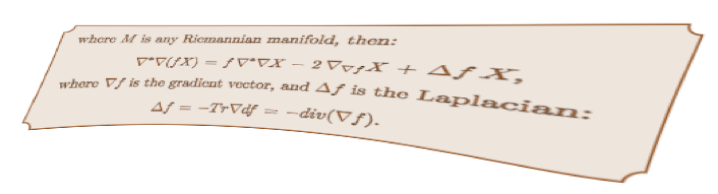
E. Vergara-Diaz & C.M. Wood, Harmonic contact metric structures, and submersions, International Journal of Mathematics 20 (2009), 209-225.  arXiv:0708.4377v1

Abstract:

We study harmonic almost contact structures in the context of contact metric manifolds, and an analysis is carried out when such a manifold fibres over an almost Hermitian manifold, as exemplified by the Boothby-Wang fibration. Two types of almost contact metric warped products are also studied, relating their harmonicity to that of the almost Hermitian structure on the base or fibre.

C.M. Wood, Bending and stretching unit vector fields in Euclidean and hyperbolic 3-space, Annals of Global Analysis and Geometry 34 (2008), 101-113.  arXiv:math/0612286v2

Abstract:

New examples of harmonic unit vector fields on hyperbolic 3-space are constructed by exploiting the reduction of symmetry arising from the foliation by horospheres. This is compared and contrasted with the analogous construction in Euclidean 3-space, using a foliation by planes, which produces some new examples of harmonic maps from 3-dimensional Euclidean domains to the 2-sphere. Finally, the unit vector field tangent to a parallel family of hyperbolic geodesics is shown to be unstable, by constructing a class of compactly supported energy-decreasing variations. All examples considered have infinite total bending.

M. Benyounes, E. Loubeau & C.M. Wood, Harmonic sections of Riemannian vector bundles, and metrics of Cheeger-Gromoll type, Differential Geometry and its Applications 25 (2007), 322-334.  math.DG/0602049

Abstract:

We study harmonic sections of a Riemannian vector bundle over a Riemannian manifold M whose total space E is equipped with a 2-parameter family of metrics h_{p,q} which includes both the Sasaki and Cheeger-Gromoll metrics. The restrictions of the h_{p,q} to the total space of any sphere subbundle SE(k) of E (where k > 0 is the sphere radius) are essentially the same for all (p,q), and it is shown that for every k there exists a unique p such that the harmonic sections of SE(k) are harmonic sections of E with respect to h_{p,q} for all q. In both the compact and non-compact cases Bernstein regions of the (p,q)-plane are identified, where the only harmonic sections of E with respect to h_{p,q} are parallel. Examples are constructed of vector fields which are harmonic sections of E = TM in the case where M is compact and has non-zero Euler characteristic.

E. Vergara-Diaz & C.M. Wood, Harmonic almost contact structures, Geometriae Dedicata 123 (2006),131-151.  math.DG/0602533

Abstract:

An almost contact metric structure is parametrized by a section of an associated homogeneous fibre bundle, and conditions for this to be a harmonic section, and a harmonic map, are studied. These involve the characteristic vector field, and the almost complex structure in the contact subbundle. Several examples are given where the harmonic section equations reduce to those for the characteristic field to be a harmonic section of the unit tangent bundle. These include trans-Sasakian structures, and certain nearly-cosymplectic structures. On the other hand, we obtain examples where the characteristic field is harmonic but the almost contact structure is not.  Many of our examples are obtained by considering hypersurfaces of almost Hermitian manifolds, with the induced almost contact structure, and comparing the harmonic section equations for both structures.

R.M. Friswell & C.M. Wood, Harmonic vector fields on pseudo-Riemannian manifolds, Journal of Geometry and Physics 112 (2017), 45-58.  arXiv:1501.01622 [math.DG]

Abstract:

The theory of harmonic vector fields on Riemannian manifolds is generalised to pseudo-Riemannian manifolds.  Harmonic conformal gradient fields on pseudo-Euclidean hyperquadrics are classified up to congruence, as are harmonic Killing fields on pseudo-Riemannian quadrics.  A para-Kaehler twisted anti-isometry is used to correlate harmonic vector fields on the quadrics of neutral signature.

M. Benyounes, E. Loubeau & C.M. Wood, Harmonic vector fields on space forms, Geom. Dedicata 177 (2015), 323-352.  arXiv:1301.6075 [math.DG]

Abstract:

A vector field on a Riemannian manifold M is said to be harmonic if there exists a member of a 2-parameter family of generalised Cheeger-Gromoll metrics on the tangent bundle with respect to which it is a harmonic section. If the manifold is a simply-connected non-flat space form other than the 2-sphere, examples are obtained of conformal vector fields that are harmonic. In particular, the harmonic Killing fields and conformal gradient fields are classified, a loop of non-congruent harmonic conformal fields on the hyperbolic plane constructed, and the 2-dimensional classification achieved for conformal fields. A classification is then given of all harmonic quadratic gradient fields on spheres.

1. A.Ramachandran & C.M. Wood, Higher-power harmonic maps and sections, 2019.
   

arXiv:1902.03134 [math.DG]

Abstract:

The variational theory of higher-power energy is developed for mappings between Riemannian manifolds and sections of submersions of Riemannian manifolds, and applied to sections of Riemannian vector bundles and their sphere subbundles.  A complete classification is given for left-invariant vector fields on 3-dimensional unimodular Lie groups equipped with an arbitrary left-invariant Riemannian metric.