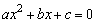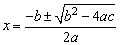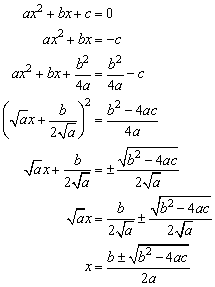Exams at York: A Few Notes for Overseas Students
Over the past few years, the number
of overseas students that have been sitting exams that I’ve
been marking has
considerably increased, particularly since I've been involved in the
new one-year MSc
here at York. Since this course has been running, I've noticed two
interesting things:
- In their first term here, the exam scores of the
overseas MSc students are significantly lower, on average, than the
exam scores of the home students.
- In the second term, the exam scores of the overseas
students are equal to, or even slightly above the exam scores of the
home students.
It's difficult to do any controlled experiments to find out
why this should be the case, but from talking to students, a few themes
consistently appear:
- The students claim the exams are a “different style to
those they have done previously".
- The students are sometimes not sure what the examiner wants
in the answer.
Despite lots of past papers being
available, it seems that a lot of students need the shock of doing badly
in an exam before they believe that there really is a difference, and they
really need to do something about it.
These few notes are designed to help avoid the shock. All
feedback very welcome.
1) Knowledge is not enough.
We want to see the ability to work with the knowledge, and of your
ability to express your opinion, backed by evidence. It seems
that some people come from Universities in which the exams are
tests of knowledge: provided you learn what's in the notes, you'll be
fine.
That's not enough here. You're likely to be asked "why" something
works, and to "discuss alternatives". For every fact you come
across, ask yourself "why is this true?" If you can't answer that
question - do some research, ask the lecturer, read some books.
You might need to know.
Don't just learn formulas. Learn when the formula is valid
(almost all engineering formulas only work for particular values of
their inputs), what assumptions were made to derive the formula (you
might be asked how accurate the formula is likely to be).
2) You have to think in an exam.
The exam questions will not be the same as in previous year, or as the
examples done during the courses. You have to be able to use
the information in the courses to solve new problems. The
best way to learn how to do this is to do as many problems as you can
find. If you run out, make up some new ones and swop them with
the other students. Ask the lecturer if you're unsure.
3) Don't panic if you can't do all of the question.
We don't expect anyone to do all of the question correctly. I know that
in some countries, 90% is a very good mark on an exam, 80% is a good mark,
70% is average, and below 60% counts as a fail.
It's very different here. It's very, very rare for anyone to get
over 90% on an exam, and probably only about 10% of students will
score more than 80%. 70% is a very good mark here, 60% is a good
mark, and it's only below 50% that you have to worry about failing.
This means that there's no need to do all of the questions to get a
very good mark. If you can do 3/4 of the question and get it right,
you'll be one of the top students.
If you think about it, the only way to find out exactly how good someone
really is, is to ask them to do something they can't do. That way you find
out where their limit is. This means we have to set some problems that we
don't expect anyone to be able to do. If you can do them - congratulations
- but please don't worry if you can't do everything. That's normal.
Especially important: if you can't do all of a question, or even all of
part of a question, don't give up. Tell us what you do know,
go as far as you can, write down your thoughts. You'll get marks
for any progress you can make. If you write nothing, you'll get
nothing.
4) Understanding what the questions mean.
For example, consider the words "derive", "explain" and "state".
They all mean different things in an exam question, and if you "state" when
you should be "deriving" you'll lose marks; and if you "explain" when you
should be "stating", you'll be wasting time. Please make sure you know the
differences.
For example:
|
Keyword
|
Example
|
How to Answer
|
|
State…
|
State the formula for the roots of a
quadratic equation
|
A very short answer is required. Just write down
|
|
Derive…
|
Derive the solution
to the
quadratic equation 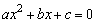
|
A long answer is required,
start from what you are told in the question, write down every step of
the algebra and every assumption you make.
|
|
…mean
|
What does the term
"quadratic equation" mean?
|
All you need to do is define
what a quadratic equation is. There's no need to even mention
how to solve it.
|
|
Explain…
|
Explain what is
meant by a "quadratic equation"
|
Same as the previous answer.
|
|
Comment on…
|
Comment on the formula:
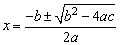
|
Quite a deep question,
requiring a long answer. This
includes an explanation of what the formula says, what it does, but
also a discussion of when the formula works, when it does not work, and
what difficulties there are in using it (e.g. imaginary roots).
|
|
Discuss..
|
Discuss quadratic equations
|
Similar to “Comment
on…”, but with more scope.
A
long answer is required. You’re
free to write anything you know about quadratic equations, including
what they are often used for, but you
should include all the points under “comment
on…” above.
|
Example solutions to these questions:
Q) What is meant by a "quadratic equation"?
A) A quadratic equation is any equation that can be expressed in the
form 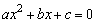 .
.
Q) State the formula for the roots of the quadratic equation:
A) 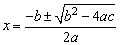
(That's all you need to put for a
"state" question. Anything else is a waste of time.)
Q) Derive the formula for the roots of the quadratic equation:
A) By using the word "derive" the examiner is asking you for:
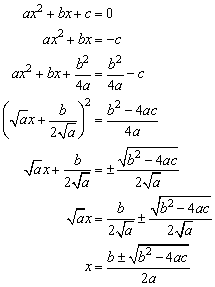
Preferably with some comments explained what you're doing.
Just writing the solution is not enough - you won't get many
marks for that.
For any question that says "derive", start with what information you
are given, and work through to the formula, showing all the steps, and
clearly stating your assumptions as you go. (For example, the
above formula doesn't work when a = 0, so you have to assume that a is
not zero.)
Q) Comment on the formula 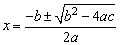
A) This is the well-known formula that finds the two roots of the
quadratic equation 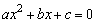 .
It can be derived by the process of completing the squares, a
process that was known to the Babylonians around 400 BCE, and to
Chinese mathematicians around 200 years later. The first explicit
statement of this equation was made by Brahmagupta in 628 CE. The
use of the solutions in the case where b2
- 4ac is negative (and hence
the equation has complex roots) was not known until much later.
It is derived using the technique of "completing the square".
.
It can be derived by the process of completing the squares, a
process that was known to the Babylonians around 400 BCE, and to
Chinese mathematicians around 200 years later. The first explicit
statement of this equation was made by Brahmagupta in 628 CE. The
use of the solutions in the case where b2
- 4ac is negative (and hence
the equation has complex roots) was not known until much later.
It is derived using the technique of "completing the square".
The formula is not used in this form in numerical algorithms, due to
the problems of loss of precision when a and c are much less
than b. In this case it is usually better to calculate the
larger of the two roots first, and then derive the second root by
dividing the ratio c/a by the first root. This indirect approach
offers greater accuracy.
and so on... [Thanks to Wikipedia for the information.]
Note that you need to know a lot more about a subject to get good marks
on a question that asks you to "comment on" or "discuss" a subject, but there is
more of a chance to show off what you do know - if you have a particular
interest in history, or computing algorithms, write about them. Either way,
you could get good marks here.