 d
d
This talk was written for a BUPA Foundation workhop on the implementation of guidelines in June 1999. It was later published as:
Bland, JM, Sample size in guidelines trials. Family Practice 2000; 17: S17-S20.
In this HTML version, I have spelt out the Greek letters "mu" and "sigma", used "root" for "square root", "*" for "multiply", and "x" for "x bar".
In the study of guidelines the main function of randomised clinical trials is to evaluate the attempt to persuade service providers such as GPs to adopt the guideline. It is not to evaluate the guideline itself. If this is soundly based on good evidence, then we know without further trial that its implementation would be beneficial to patients. It follows that the appropriate unit of analysis of the trial is not the patient, but the doctor.
In this paper I shall outline the statistical concepts of significance and power and the way in which they are used in the determination of sample size for trials. I shall then go on to show how this must be modified to deal with the designs met in guideline research. These are called cluster-randomized trials, because the patients of a single doctor or practice form a single unit called a cluster.
As we shall see, approaches to design and analysis which ignore the clustering may be highly misleading.
In a typical clinical trial, we allocate our subjects into two groups at random. These groups then form two samples from the same population. We apply different treatments to the two samples. If the treatments have the same effect, we still have samples from the same population, if not, the samples are now from different populations. For example, we might randomize general practices into two groups and provide one group with guidelines. We measure the extent to which each practice conforms to the guidelines. We then use a significance test to test the null hypothesis that the groups are from the same population, i.e. that the treatment has had no effect.
A typical test of significance works like this. Suppose we have two populations with means mu1 and mu2, standard deviation sigma, all unknown. We have two samples, each size n, with means x1 and x2, and standard deviation s. The details, including the effects of unequal sample sizes, unequal variances, small samples, etc., are given in many books (Armitage and Berry 1994, Altman 1991, Bland 1995, Machin et al. 1998).
The difference between x1 and x2 would vary
from sample to sample. If we were to do the experiment again, we would get
different means. These might not differ in the same way; indeed, they might
differ in the opposite direction. We want to know whether the difference in
our sample is large enough for us to conclude that there is a difference in the
whole population. This is the function of the test of significance. For one
such test, the large sample z test, we calculate:
z = (x1 - x2) / root(2s2/n)
If there were no population difference, this would be an observation from a
standard Normal distribution. If its absolute value exceeds 1.96, the
difference is significant at the 5% level.
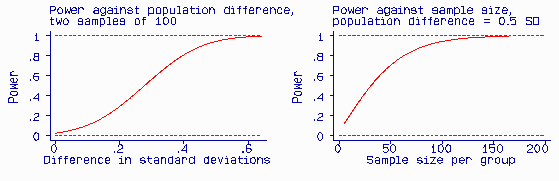
The test is more likely to give a significant difference if there is a large difference between the two populations than a small one. It is also more likely to detect a population difference of a given size (i.e. be significant) if the sample is large than if it is small. We call the probability that a test will produce a significant difference at a given significance level the power of the test. Power is related to the postulated difference in the population, the sample size, and the significance level (alpha = 0.05). The Figure shows the effect of hypothesized population difference and sample size on the power of a test.
A simple formula connects the number in each group, the significance level
alpha, the power P, the hypothesized difference mu1
- mu2 and the variance sigma2:
n = f(alpha,P) * 2 sigma2 / (mu1 -
mu2)2
Here f(alpha,P) is a simple function of alpha and P
derived from the Normal distribution, tabulated below:
| Power, P | Significance level, alpha | |
|---|---|---|
| 0.05 | 0.01 | |
| 0.50 | 3.8 | 6.6 |
| 0.70 | 6.2 | 9.6 |
| 0.80 | 7.9 | 11.7 |
| 0.90 | 10.5 | 14.9 |
| 0.95 | 15.2 | 20.4 |
| 0.99 | 18.4 | 24.0 |
The usual value used for alpha is 0.05, and P is usually 0.80 or 0.90.
Thus, to determine sample size, we need to choose the power, P, and the significance level, alpha, know the standard deviation, sigma, and decide the population difference to be detected, mu1 - mu2. The significance is usually set to 0.05 and the power to 0.90 or 0.80. Personally, I think 0.80 is too low, but most funding organisations seem happy with it. Researchers are often unable to decide on the size of difference they wish to detect. I think that they often choose the number of subjects they think they can get then calculate the target difference from that. They are often unable even to provide the standard deviation, but a pilot study can usually discover this.
In a cluster randomized study, a group of subjects are randomized to the same treatment together. For example, we might randomize GPs to receive guidelines or not. The patients of the GP or of the whole practice form the cluster. An example is given in the following Table:
| Guidelines | Control | |||||
|---|---|---|---|---|---|---|
| Number of requests | Percent conforming | Number of requests | Percent conforming | |||
| Total | Conforming | Total | Conforming | |||
| 20 | 20 | 100 | 7 | 7 | 100 | |
| 7 | 7 | 100 | 37 | 33 | 89 | |
| 16 | 15 | 94 | 38 | 32 | 84 | |
| 31 | 28 | 90 | 28 | 23 | 82 | |
| 20 | 18 | 90 | 20 | 16 | 80 | |
| 24 | 21 | 88 | 19 | 15 | 79 | |
| 7 | 6 | 86 | 9 | 7 | 78 | |
| 6 | 5 | 83 | 25 | 19 | 76 | |
| 30 | 25 | 83 | 120 | 90 | 75 | |
| 66 | 53 | 80 | 89 | 64 | 73 | |
| 5 | 4 | 80 | 22 | 15 | 68 | |
| 43 | 33 | 77 | 76 | 52 | 68 | |
| 43 | 32 | 74 | 21 | 14 | 67 | |
| 23 | 16 | 70 | 127 | 83 | 66 | |
| 64 | 44 | 69 | 22 | 14 | 64 | |
| 6 | 4 | 67 | 34 | 21 | 62 | |
| 18 | 10 | 56 | 10 | 4 | 40 | |
| Total | 429 | 341 | 704 | 509 | ||
| Mean | 81.6 | 73.6 | ||||
| SD | 11.9 | 13.1 | ||||
(Oakeshott et al. 1994, Kerry and Bland 1998a.)
The analysis must take the clustering into account. Ignoring it may make confidence intervals far too narrow and P values too small, resulting in spurious significant differences. This is done far too often. This should not surprise us, as cluster randomization has been ignored almost completely in textbooks of medical statistics and in statistical articles in the medical literature. Only recently have medical statisticians begun to publish guidance on this (Bland and Kerry 1997, Kerry and Bland 1998b, 1998c). For example, the first edition of Statistical Tables for the Design of Clinical Trials (Machin and Campbell 1987) did not include them, but the second edition does (Machin et al. 1998). Several methods of analysis can be used. The simplest is to combine the data for the patients from one practice into a single summary statistic (Kerry and Bland 1998a; Kerry and Bland 1998b). The patients here tell us something about the practice, and the proportion of referrals from the practice which conform to the guidelines provides a good measure of the practice conformity. We can then carry out a two sample t test on summary statistics. In the table of the X-ray data above, the numbers of referrals in the clusters varies considerably. We can do a t test weighted by cluster size to take this into account (Bland and Kerry 1998). We may need to use a transformation to make the data approximately Normal. Another approach is multilevel modelling (Goldstein 1995), which increases the complexity considerably. As the focus of the analysis is here on the practitioner rather than the patients, this is seldom necessary.
The presence of clusters alters the calculation of the sample size (Kerry and
Bland 1998c). We now have two different sample sizes: the number of clusters
(practices), c, and the number of subjects (patients) within a cluster,
m. We also have two different variances: the variance between clusters,
sigmac2, and the variance within a cluster,
sigmaw2. The formula for sample size now gives us
the number of clusters required and becomes:
c = f(alpha,P) * 2 ( sigmac2 +
sigmaw2/m) / (mu1 -mu2)2
The total number of patients is n = cm.
The ratio of the total number of subjects required using cluster randomization
to the number required using simple randomization is called the design
effect.
Deff = (m sigmac2 + sigmaw2) /
(sigmac2 + sigmaw2)
We can calculate the sample size as for a simply randomized (non-cluster) study
and multiply it by Deff to get the number of subjects required for the cluster
design.
It can be useful to present the design effect in terms of the intra-cluster
correlation coefficient (ICC):
ICC = sigmac2 / (sigmac2 +
sigmaw2 )
This is the correlation which we expect between observations on pairs of
subjects drawn one pair from each cluster. The design effect is then
Deff = 1 + (m-1) ICC
To estimate our sample size we need an estimate not just of the variance of our
measurement between subjects but we also need an estimate of the between
cluster variation or the ICC. Although ICCs in cluster-randomized trials are
often small, typically less than 0.1, their effect cannot be ignored. For
example, if ICC=0.05 and the cluster size is m = 30, then Deff=2.45.
The number of patients required is more than twice that for a trial where
patients were randomized individually.
Although the focus of a guidelines study must be on the service provider, we still need to consider the number of subjects in the cluster, the patients used to provide information about the provider. To do this we need information on the two variances, in particular the variance between-clusters, or on the ICC. This may be difficult to come by.
Thanks to my collaborator Sally Kerry for many helpful discussions and for supplying the data.
Altman, D.G. (1991) Practical Statistics for Medical Research Chapman and Hall, London.
Armitage, P., Berry, G. (1994) Statistical Methods in Medical Research, Third Edition Blackwell, Oxford.
Bland, J.M., Kerry, S.M. (1997) Statistics Notes. Trials randomized in clusters. British Medical Journal 315, 600.
Bland, J.M., Kerry, S.M. (1998) Statistics Notes. Weighted comparison of means. British Medical Journal 316 129.
Bland, M. (1995) An Introduction to Medical Statistics, Second Edition Oxford University Press, Oxford.
Goldstein, H. (1995) Multilevel statistical models, Second Edition Arnold, London.
Kerry, S.M., Bland, J.M. (1998a) Statistics Notes. Analysis of a trial randomized in clusters. British Medical Journal 316, 54.
Kerry, S.M., Bland, J.M. (1998b) Trials which randomize practices 1: how should they be analysed? Family Practice 15, 80-83.
Kerry, S.M., Bland, J.M. (1998c) Trials which randomize practices 2: sample size. Family Practice 15, 84-87.
Machin, D., Campbell, M.J. (1987) Statistical Tables for the Design of Clinical Trials Oxford, Blackwell.
Machin, D., Campbell, M.J., Fayers, P., Pinol, A. (1998) Statistical Tables for the Design of Clinical Studies, Second Edition Oxford, Blackwell.
Oakeshott, P., Kerry, S.M., Williams, J.E. (1994) Randomised controlled trial of the effect of the Royal College of Radiologists' guidelines on general practitioners' referral for radiographic examination. British Journal of General Practice 44, 197-200.
Back to clustered study designs menu.
Back to full length papers and talks menu.
Back to Martin Bland's Home Page.
This page maintained by Martin Bland.
Last updated: 6 April 2004.