Correction to section "Measuring agreement using repeated measurements" in Bland and Altman (1986)

This is a corrected version of the secion "Measuring agreement using repeated measurements" in Bland and Altman (1986) Statistical methods for assessing agreement between two methods of clinical measurement (Lancet, i, 307-310). The mistake was spotted by Jan Vandenbroucke, to whom I am very grateful.

SAMPLE DATA

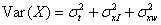
The sample comprised colleagues and family of J.M.B. chosen to give a wide range of PEFR but in no way representative of any defined population. Two measurements were made with a Wright peak flow meter and two with a mini Wright meter, in random order. All measurements were taken by J.M.B., using the same two instruments. (These data were collected to demonstrate the statistical method and provide no evidence on the comparability of these two instruments.) We did not repeat suspect readings and took a single reading as our measurement of PEFR. Only the first measurement by each method is used to illustrate the comparison of methods, the second measurement being used in the study of repeatability.

PEFR MEASURED WITH WRIGHT PEAK FLOW AND MINI WRIGHT PEAK FLOW METER
Wright peak flow meter Mini Wright peak flow meter
First PEFR Second PEFR First PEFR Second PEFR
Subject (l/min) (l/mi) (l/min) (l/min)
1 494 490 512 525
2 395 397 430 415
3 516 512 520 508
4 434 401 428 444
5 476 470 500 500
6 557 611 600 625
7 413 415 364 460
8 442 431 380 390
9 650 638 658 642
10 433 429 445 432
11 417 420 432 420
12 656 633 626 605
13 267 275 260 227
14 478 492 477 467
15 178 165 259 268
16 423 372 350 370
17 427 421 451 443

MEASURING AGREEMENT USING REPEATED MEASUREMENTS

If we have repeated measurements by each of the two methods on the same subjects we can calculate the mean for each method on each subject and use these pairs of means to compare the two methods using the analysis for assessing agreement described above. The estimate of bias will be unaffected, but the estimate of the standard deviation of the differences will be too small, because some of the effect of repeated measurement error has been removed. We can correct for this. Suppose we have two measurements obtained by each method, as in the table. We find the standard deviation of differences between repeated measurements for each method separately, s1 and s2, and the standard deviation of the differences between the means for each method, sD. The corrected standard deviation of differences, sc, is √(sD2 + 1/2 s12 + 1/2 s22). This is approximately √(2sD2), but if there are differences between the two methods not explicable by repeatability errors alone (i.e. interaction between subject and measurement method) this approximation may produce an overestimate. For the PEFR, we have sD = 33.2, s1 = 21.6, s2 = 28.2 l/min. sc is thus √(33.22 + 1/2 × 21.62 + 1/2 × 28.22) or 41.6 l/min. Compare this with the estimate 38.8 l/min which was obtained using a single measurement. On the other hand, the approximation √(2sD2) gives an overestimate (47.0 l/min).

What was the mistake?

In the Lancet paper we gave the formula as sc, is √(sD2 + 1/4 s12 + 1/4 s22).

This formula was given correctly in Bland JM, Altman DG. (1999) Measuring agreement in method comparison studies. Statistical Methods in Medical Research 8, 135-160.

I think that I was to blame for this mistake, though I have no idea how it came about. It was a long time ago. Sorry about that. However, people who never make mistakes seldom make anything. If you notice that I have made a mistake, please let me know. Sooner or later, I will try to correct it.

How is the correct formula derived?

This is an extract from Bland and Altman (1999), Section 5.1, "Equal numbers of replicates".

When we make repeated measurements of the same subject by each of two methods, the measurements by each method will be distributed about the expected measurement by that method for that subject. These means will not necessarily be the same for the two methods. The difference between method means may vary from subject to subject. This variability constitutes method times subject interaction. Denote the measurements on the two methods by X and Y. We are interested in the variance of the difference between single measurements by each method, D = X – Y. If we partition the variance for each method we get

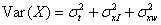
Equation: Var bracket X bracket = sigma sub t squared + sigma sub x I squared + sigma sub x w squared.

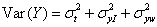
Equation: Var bracket Y bracket = sigma sub t squared + sigma sub y I squared + sigma sub y w squared.

where σt2 is the variance of the true values, σxI2 and σyI2 are method times subject interaction terms, and σxw2 and σyw2 are the within-subject variances from measure-ments by the same method, for X and Y, respectively. It follows that the variance of the between-subject differences for single measurements by each method is

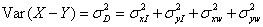Equation: Var bracket X minus Y bracket = sigma sub D squared = sigma sub x I squared + sigma sub y I squared + sigma sub x w squared + sigma sub y w squared.         (1)

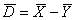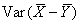We wish to estimate this variance from an analysis of the means of the measurement for each subject, Equation: D bar = X bar minus Y bar., that is from Equation: D bar = X bar minus Y bar.. With this model, the use of the mean of replicates will reduce the within-subject variance but it will not affect the interaction terms, which represent patient-specific differences. We thus have

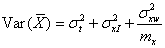
Equation: Var bracket X bar bracket = sigma sub t squared + sigma sub x I squared + fraction sigma sub x w squared over m sub x.

where mx is the number of observations on each subject by method X, because only the within-subject within-method error is being averaged. Similarly

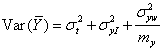
Equation: Var bracket Y bar bracket = sigma sub t squared + sigma sub y I squared + fraction sigma sub y w squared over m sub y.

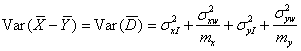
Equation: Var bracket X bar minus Y bar bracket = sigma sub D bar squared = sigma sub x I squared + fraction sigma sub x w squared over m sub x + sigma sub y I squared + fraction sigma sub y w squared over m sub y.

The distribution of 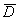Equation: D bar. depends only on the errors and interactions, because the true value is included in both X and Y, which are differenced. It follows from equation (1) that

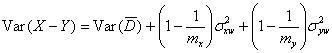
Equation: Var bracket X minus Y bracket = Var bracket D bar bracket + bracket one minus fraction one over m sub x bracket sigma sub x w squared + bracket one minus fraction one over m sub x bracket sigma sub y w squared.

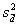If Equation: s sub d bar squared. is the observed variance of the differences between the within-subject means, 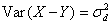Equation: Var bracket X minus Y bracket = sigma sub d squared. is estimated by

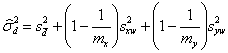
Equation: sigma hat sub d squared = s sub d bar squared + bracket one minus fraction one over m sub x bracket s sub x w squared + bracket one minus fraction one over m sub y bracket s sub y w squared.

In the common case with two replicates of each method we have

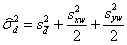
Equation: sigma hat sub d squared = s sub d bar squared + fraction s sub x w squared over two + fraction s sub y w squared over two.

as given in the correction above.

Back to Publications on comparing two methods of medical measurement.

Back to Comparing two methods of medical measurement menu.

Back to Martin Bland's home page.

This page maintained by Martin Bland.
Last updated: 3 July, 2009.

Back to top.