 d
d
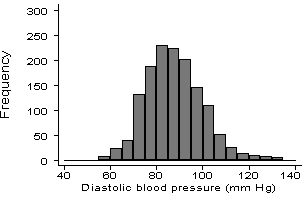
In a study of blood pressure in one town, the distribution of diastolic blood pressure among men was shown as follows (British Medical Journal 1974; 3: 600-3):
Infants who died from Sudden Infant Death Syndrome (SIDS or cot death) were compared to a group of live infants, matched for age and birthweight. The temperature in the babyís bedroom and the amount of thermal insulation (clothes and bedding) were measured, to give an estimate of the excess thermal insulation. The dead children had had more excess thermal insulation (mean 2.3 togs, standard deviation 3.4 togs) than the live children (mean 0.6 togs, standard deviation 2.3 togs) (British Medical Journal 1992; 304: 277-82).
The following extract is from Hansard, 29 November 1991, quoted in the Royal Statistical Society's News and Notes, 1992 vol 18(7), page 12. (Hansard is the official record of the Parliament of the United Kingdom.) The idea which Members of Parliament are discussing is that a minimum wage would be defined as a fixed proportion of the median wage.
Mr Arbuthnot: . . . suggestion of a minimum wage is in itself rather obscure and bizarre. As I understand it, it is tied to the average and would therefore not only be relatively high at £3.40, but would increase as the average wage itself increased. With each increase in the average rate of pay, the minimum wage itself would have to go up and it would be forever chasing its own tail.
Mr Tony Lloyd: Perhaps I can help the Hon. Gentleman. It will be tied to the median, which is not the same as the average. It is simply the mid-point on the range and would not be affected by changes in the minimum wage.
Mr Arbuthnot: From what I understand, even an amount tied to the median would be affected because if the lowest wage were increased to £3.40 per hour, the median would have to rise.
Mr Tony Lloyd: I shall put the matter in simple terms. The median, the mid-point in a series of numbers such as 2, 2, 5, 6 and 7, is defined as being the difference between 2 and 7, which is 3.5. If we alter the figures 2 and 2 to 3.5, the middle figure of 5 would remain unaltered because it is independent of the bottom figures.
Mr Arbuthnot: I do not understand the Hon. Gentlemanís mathematics and I slightly doubt whether he does.
Mr Matthew Carrington: I am extremely confused. I studied mathematics for some years at school and I have not totally forgotten all of them. The median is not the mid-point between the first number and the last. It is where the largest number of items in a sample comes to, whereas the average is obviously the sample multiplied by the number of items. The Hon. Member for Stretford (Mr Lloyd) is obviously extremely confused. The median has a precise mathematical definition which is absolutely right, and my Hon. Friend is correct in saying that the median is bound to alter if the number at the bottom of the scale is changed. That will alter the average as well in a different way, but it is bound to alter the median. Perhaps the Hon. Member for Stretford wishes to define median in a non-mathematical sense.
Mr Arbuthnot: I am extremely grateful to my Hon. Friend for sorting out at least the Hon. Gentlemanís mathematics with obvious skill and knowledge.
(Questions taken from Martin Bland and Janet Peacock: Statistical Questions in Evidence-based Medicine, Oxford University Press, Oxford, 2000.)
To Introduction to Statistics for Research index.
This page maintained by Martin Bland.
Last updated: 13 January, 2020.