|
PB Karadakov's Research
|
Recent Work |
|
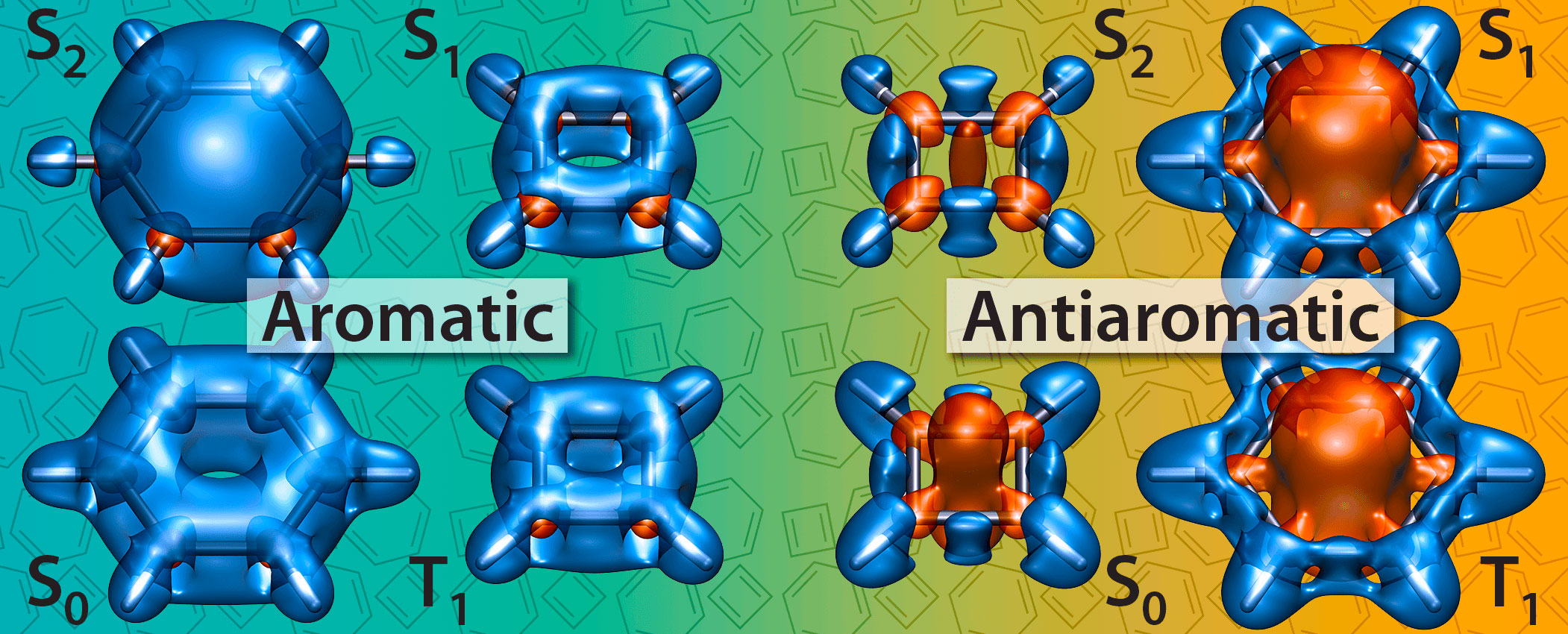
P. B. Karadakov, P. Hearnshaw and K. E. Horner, Magnetic Shielding, Aromaticity, Antiaromaticity and Bonding in the Low-Lying Electronic States of Benzene and Cyclobutadiene, J. Org. Chem. 81 (2016) 11346-11352.
|
|
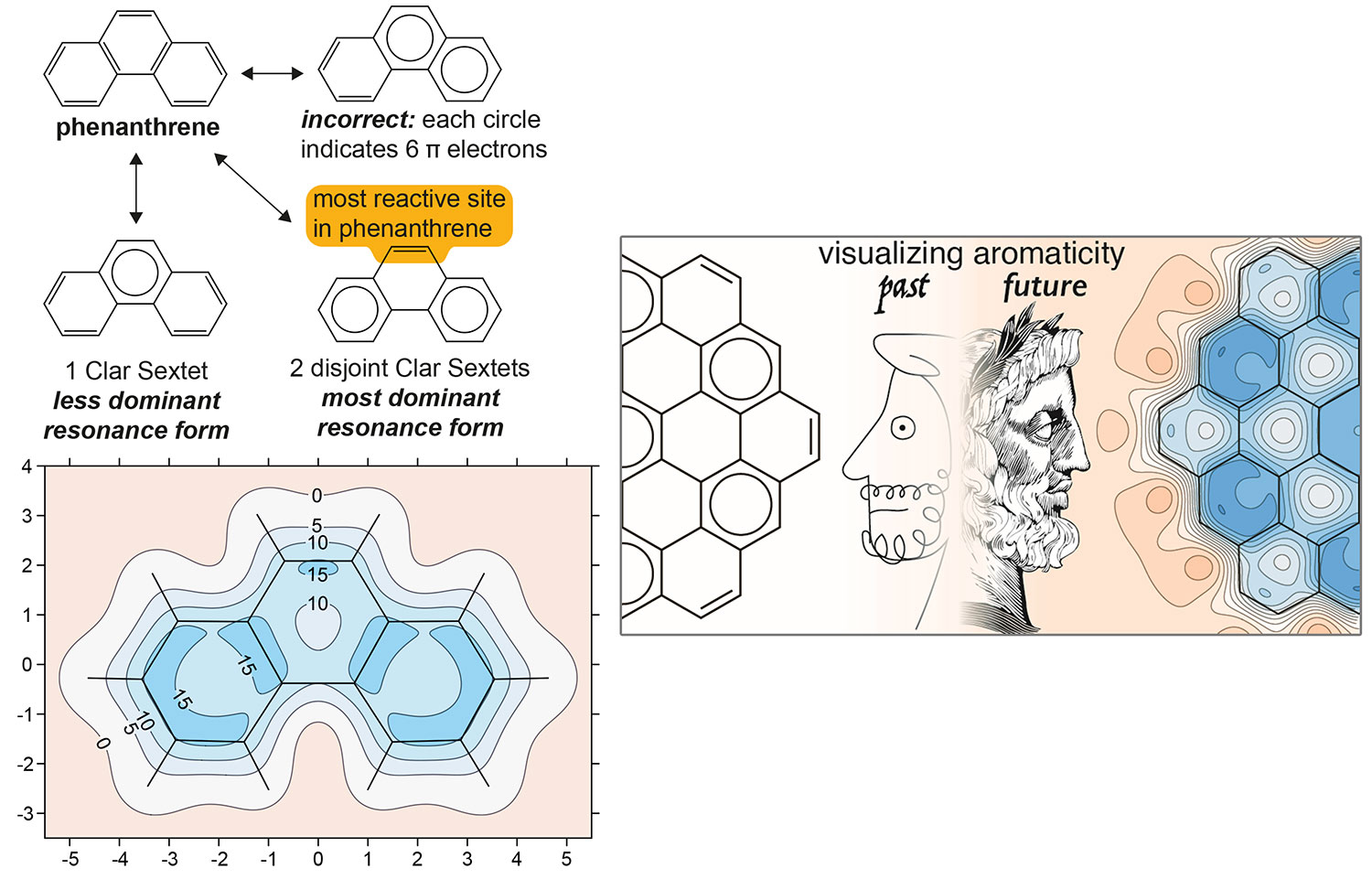
B. J. Lampkin, P. B. Karadakov and B. VanVeller, Detailed Visualization of Aromaticity Using Isotropic Magnetic Shielding, Angew. Chem. Int. Ed. 59 (2020) 19275-19281.
|
|
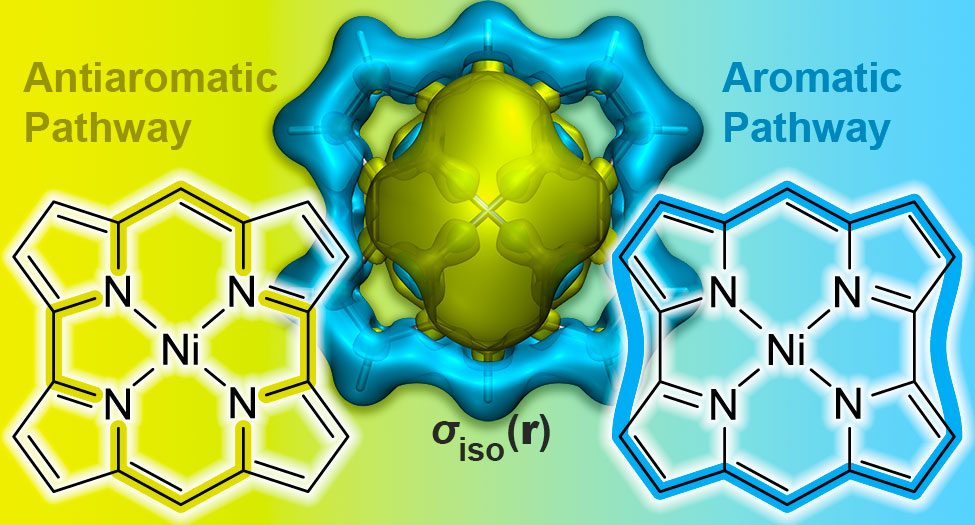
P. B. Karadakov, Norcorrole: Aromaticity and Antiaromaticity in Contest, Org. Lett. (2020) 22 (2020) 8676-8680.
|
|
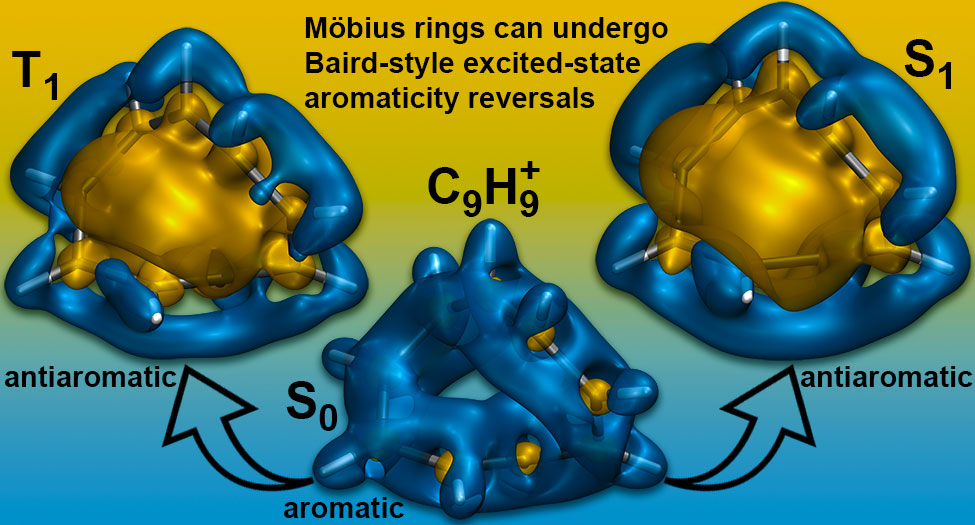
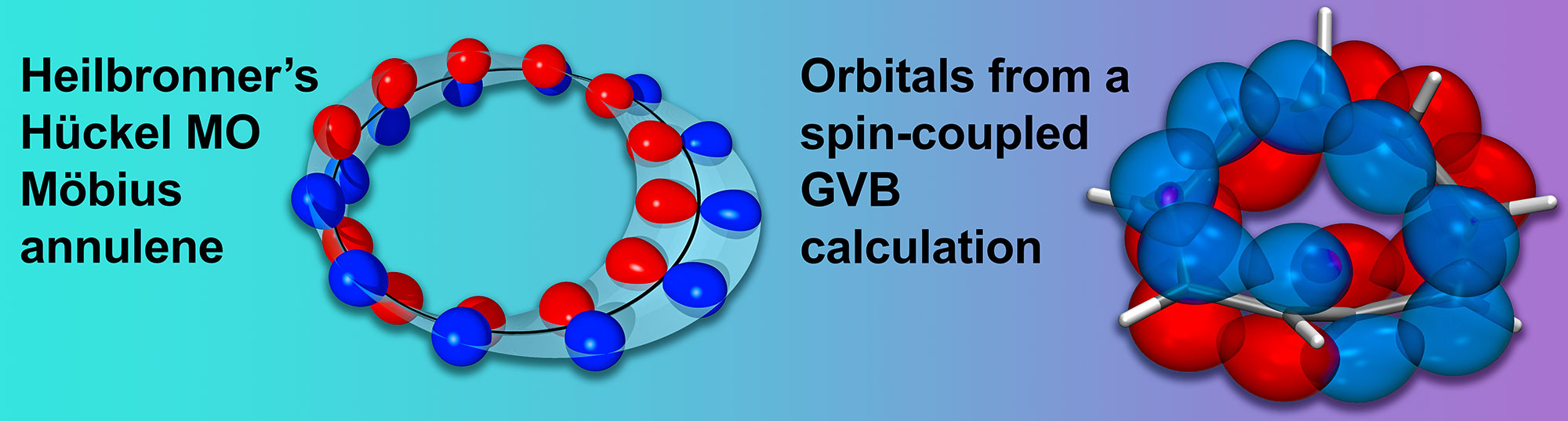
P. B. Karadakov and D. L. Cooper, Excited-state Aromaticity Reversals in Möbius Annulenes, J. Phys. Chem. A 124 (2020) 9611-9616.
|
|
P. B. Karadakov and D. L. Cooper, Does the Electronic Structure of Möbius Annulenes Follow Heilbronner's Ideas?, ChemPhysChem 19 (2018) 3186-90.
|
|
P. B. Karadakov, M. A. H. Al-Yassiri and D. L. Cooper, Magnetic Shielding, Aromaticity, Antiaromaticity and Bonding in the Low-Lying Electronic States of S2N2, Chem. Eur. J. 24 (2018) 16791-16803.
|
Research Interests & Older Work |
|
My research interests are in the area of molecular electronic structure theory and involve methodological work and code development, as well as theoretical studies of bonding, reactivity and other electronic properties of molecular systems in organic, inorganic chemistry and materials science. |
Modern Valence-Bond Theory |
|
In the hands of an experienced researcher, modern computer implementations of advanced molecular orbital (MO) approaches (GAUSSIAN, GAMESS-US, GAMESS-UK, etc) can provide reliable ab initio descriptions of a variety of molecules and chemical reactions. The results are usually of excellent quantitative value but, as a rule, it is very difficult to interpret them using qualitative terms related to electron pairs and unpaired electrons which are amongst the basic elements of chemical thinking about the structure of atoms and molecules and their interactions. Concepts that utilize these terms, for example, the Lewis theory of valence [the precursor to classical valence bond (VB) theory], still have a considerable impact on most areas of chemistry. However, advanced MO theory is gradually moving away from being able to provide these very useful ideas and concepts with a solid theoretical background.
The spin-coupled (SC) approach [suggested in J. Gerratt and W. N. Lipscomb, Proc. Natl. Acad. Sci. (USA) 59 (1968) 332; see also J. Gerratt, Adv. At. Mol. Phys. 7 (1971) 141] combines within a single formalism the interpretational facilities of the classical VB picture and the quantitative nature of advanced MO approaches. The basic idea behind SC theory is that the wave function for the electrons in a molecule is constructed from orbitals associated with the atoms that make up the molecule which, of course, is one of the cornerstones of classical VB theory. But the SC formalism goes further and introduces two new elements of crucial importance:
This results in the emergence, in many molecules, of highly directed bonds (as a rule, a single bond is decribed by a pair of strongly overlapping hybrid-like orbitals), and of a spin-coupling pattern that bears close resemblance to classical VB resonance. The final outcome combines a unique clarity of insight into the fundamental physics and chemistry of bonding with good accuracy: In most cases, the SC wavefunction with N active orbitals recovers more than 90% of the correlation energy incorporated in a state-of-the art 'N in N' (N electrons in N active orbitals) complete-active-space self-consistent (CASSCF) field wavefunction. A now classical example that illustrates the most significant advantages of the SC approach is provided by the SC description of the p-electrons in benzene [D.L. Cooper, J. Gerratt and M. Raimondi, Nature 323 (1986) 699]. The central moments in my work on modern VB methodology are
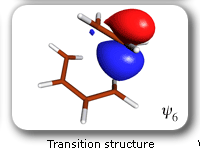
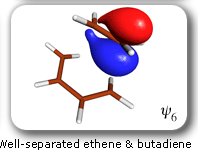
These developments have opened the way to a large number of applications [for reviews, see J. Gerratt, D.L. Cooper, P.B. Karadakov and M. Raimondi, Chem. Soc. Rev. 26 (1997) 87; P.B. Karadakov, Ann. Rep. Prog. Chem., Sect. C 94 (1998) 3]. Amongst these, of particular interest is the use of SC theory, in combination with CASSCF-level intrinsic reaction coordinate (IRC) calculations, to study the electronic mechanisms of chemical reactions. As a first example, let us consider the mechanism of the gas-phase Diels-Alder reaction between butadiene and ethene [P.B. Karadakov, D.L. Cooper and J. Gerratt, J. Am. Chem. Soc. 120 (1998)]. The spin-coupled wavefunction for the reacting system involves 6 active (or spin-coupled) and 20 inactive (or core) orbitals. There are five independent ways in which the spins of the active orbitals can be coupled together to yield an overall singlet. The closest-quality CASSCF wavefunction which can be used for the calculation of the intrinsic reaction coordinate is of the '6 in 6' type (6 electrons in 6 orbitals). The initial geometry of the reacting system in an IRC calculation is that of a transition structure (TS). Starting from the TS, the IRC can be followed in two directions: towards reactants and towards the product. Each point on the IRC corresponds to a definite geometry of the reacting system. In order to follow the evolution of the electronic structure of the reacting system, we performed a series of SC calculations at subsequent points from the IRC. |
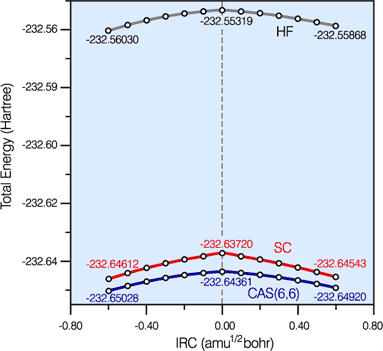 |
Hartree-Fock (HF), '6 in 6' CASSCF and spin-coupled (SC) energy profiles along the '6 in 6' CASSCF IRC for the Diels-Alder reaction.
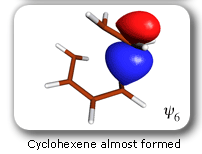
The SC and '6 in 6' CASSCF curves are very close together and much below the HF curve. The amount of '6 in 6' CASSCF correlation energy recovered by the SC wavefunction is rather uniform: 95.4% and 95.8% at the cyclohexene (-) and butadiene+ethene (+) ends of the IRC segment, respectively, and 92.9% at the TS. This demonstrates the quantitative character of the SC wavefunction and justifies its use for the definition of a reaction mechanism. |
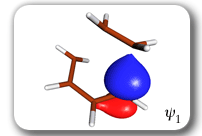
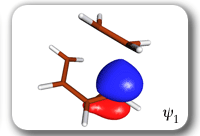
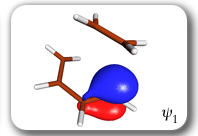
|
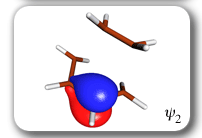
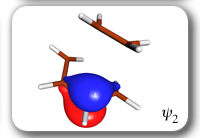
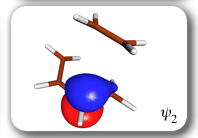
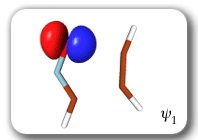
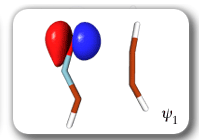
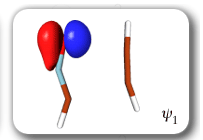
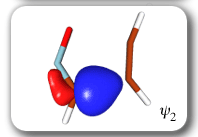
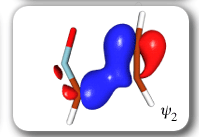
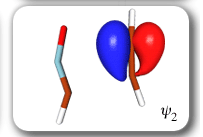
Each of the six nonorthogonal spin-coupled orbitals for the Diels-Alder reaction (see below) remains distinctly associated with a single carbon atom throughout the whole process. However, their forms adjust to accommodate the differences in the nature of bonding between reactants and products. At the TS, the shapes of orbitals 2 and 3 strongly resemble the shapes of the SC orbitals in benzene (3 is not shown, reflect 2 through the symmetry plane passing through the middle of the central butadiene C-C bond and the middle of the ethene C-C bond to obtain 3; analogous reflections of 1 and 6 result in orbitals 4 and 5, respectively). At the same time, the overlaps between all neighbouring SC orbitals become very similar and almost identical to the corresponding overlap in benzene.
|
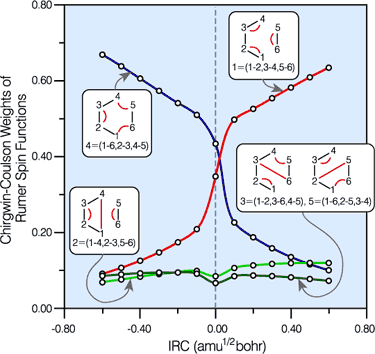 |
Spin-coupling pattern or 'resonance' along the intrinsic reaction coordinate for the Diels-Alder reaction.
The five spin eigenfunctions (see the yellow boxes) are of the Rumer type. Each of these spin eigenfunctions represents a product of three singlet two-electron spin functions. For example, in (1-2,3-4,5-6) the singlet pairs couple the spins of electrons 1 and 2, 3 and 4, and 5 and 6. The diagrams for spin eigenfunctions 1 and 4 are very similar to the two well-known equivalent Kekulé resonance structures for benzene. The weights of spin eigenfunctions 1 and 4 become identical very near to the TS. |
|
Thus, we have a geometry of the reacting system at which
The straightforward conclusion is that the Diels-Alder reaction passes through an aromatic reaction intermediate. The changes within the SC wavefunction during the Diels-Alder cycloaddition are consistent with a 'homolytic' mechanism, in which all SC orbitals participating in the bonds being reformed remain permanently attached to one and the same carbon atom throughout the reaction (see below). Information of this type cannot be provided by the HF wavefunction because of the double occupancy of all orbitals; although it is embedded inside the CASSCF wavefunction, in order to obtain it one would need to perform a transformation of the CASSCF wavefunction to a VB-style (in fact, SC-style!) representation [see e.g. T. Thorsteinsson, D.L. Cooper, J. Gerratt, P.B. Karadakov and M. Raimondi, Theor. Chim. Acta 93 (1996) 343]. |
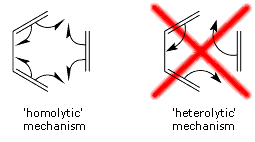 |
In many recent organic chemistry textbooks one can find a picture of the second, 'heterolytic', scheme only, accompanied by a safeguarding remark that the scheme is not meant to illustrate the real reaction mechanism (which does make one wonder why it should be there in the first place). Our results indicate that this 'heterolytic' picture is, in fact, misleading and if one needs to use a simplistic representation of the mechanism of the Diels-Alder cycloaddition, the 'homolytic' scheme would be a much better choice.
|
|
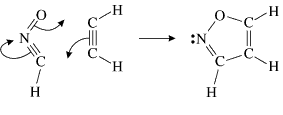
As a second example, let us have a look at the gas-phase 1,3-dipolar cycloaddition of fulminic acid to ethyne. The concerted, almost synchronous nature of this reaction might create the impression that its electronic mechanism should be very similar to that of the Diels-Alder reaction. Such an expectation is reinforced by frontier orbital theory, which treats both reactions in very much the same way. The only significant differences are related to the fact that the lowest unoccupied MO (LUMO) for a linear 1,3-dipole has a node at one of the terminal heavy atoms. This LUMO is ignored in frontier orbital theory, which considers instead the next lowest unoccupied MO.
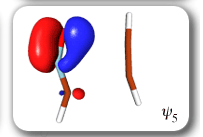
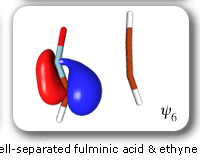
In spite of these anticipated great similarities, the results of our SC calculations [with 6 active orbitals, on top of the '6 in 6' CASSCF IRC, see P.B. Karadakov, D.L. Cooper and J. Gerratt, Theor. Chem. Acc. 100 (1998) 222] reveal a completely different picture. When the reacting molecules are far apart (see the rightmost column in the next picture), the orbitals on the HCNO fragment (orbitals 1, 3, 5 and 6) reproduce the well-known SC model for the electronic structure of 1,3-dipoles, according to which the central heavy atom is 'hypervalent' [see e.g. D.L. Cooper, J. Gerratt, M. Raimondi and S. C. Wright, J. Chem. Soc. Perkin Trans. II (1989) 1187]. The nitrogen atom in HCNO appears to take part in more than four covalent bonds: an almost triple bond between C and N (orbitals 3 and 6 account for one of the components of this bond, which would be of sigma symmetry in linear HCNO), a pi bond between N and O, and a highly polar bond between N and O (of sigma symmetry in linear HCNO, described here by orbitals 1 and 5. The remaining two orbitals, 2 and 4, form the ethyne bond (of pi symmetry in linear C2H2) that is broken during the reaction.
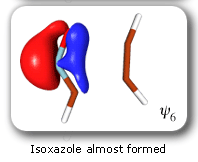
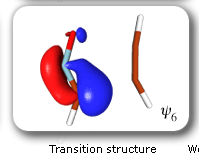
The clearest representation of the spin-coupling pattern at this stage of the cycloaddition process is achieved by reordering the SC orbitals so as to arrange in pairs the orbitals involved in the three bonds: 2 and 4, 6 and 3, and 5 and 1. The spin-coupling pattern for the reordered orbital set is largely dominated by its 'perfect-pairing' component, in which the spins associated with the pairs of orbitals (2, 4), (6, 3) and (5, 1) are coupled to singlets. The composition of the active space spin function changes very little throughout the cycloaddition process; this indicates that these orbital pairs are preserved all the way from reactants to product. As a consequence, all essential features of the SC model for the electronic mechanism of the reaction between HCNO and C2H2 are contained entirely within the variations of the shapes of the SC orbitals. For each of the orbital pairs (2, 4) and (5, 1), the shape of one orbital changes in a very dramatic fashion along the reaction coordinate. Orbital 2, which enters the reaction as one of two orbitals involved in the in-plane ethyne 'pi' bond, becomes similar at the TS to a linear combination of two spx hybrids, one at its 'original' ethyne carbon and another at the HCNO carbon. After the TS, this orbital loses its connection with the ethyne carbon and shifts entirely onto the HCNO carbon. The other orbital within this pair, orbital 4, undergoes a 're-hybridization' reminiscent of that for orbital 6 in the case of the Diels-Alder reaction. As a result, orbitals 2 and 4 become responsible, after the TS (see the leftmost column in the picture) for one of the two bonds closing the isoxazole ring. SC orbital 5 starts as one of the orbitals from the in-plane polar 'p' N-O bond in HCNO, but then, in a similar fashion to orbital 4, attains at the TS a shape that resembles a mixture of two spx hybrids, one of which is at its original location (the oxygen atom) and the other at the incoming ethyne carbon. After the TS, this orbital becomes associated primarily with the ethyne carbon. The shape of the second orbital in this pair, orbital 2, changes very little throughout the reaction. After the TS, orbitals 5 and 1 account for the second bond closing the isoxazole ring. The 'laziest' orbital pair consists of orbitals 3 and 6, which initially form the in-plane C-N 'pi' bond in HCNO. These orbitals shift very little, so as to form a nonbonding pair on the isoxazole nitrogen, partially polarized towards the oxygen atom.
The SC description of the 1,3-dipolar cycloaddition of fulminic acid to ethyne is very different from that of the Diels-Alder reaction between butadiene and ethene. The changes in the SC wavefunction during the Diels-Alder reaction are in good agreement with the principles of classical VB theory. From reactants to product, each of the six SC orbitals remains distinctly associated with a single atomic centre, and while the changes in the shapes of the orbitals provide very useful information about the evolution of the bonding interactions, an equally important role is played by the spin-coupling pattern. This last switches gradually from a form more suited to reactants to a form appropriate for the product, becoming very reminiscent, near the TS, of classical VB resonance for benzene. However, such a classical VB element is all but absent from the SC model for the 1,3-dipolar cycloaddition. Instead, the bond rearrangement is achieved by the movement of singlet-coupled orbital pairs through space, during which at least one of the orbitals within a pair becomes completely detached from the atomic centre with which it is associated initially and ends up localized about another centre. The ability of the SC wavefunction to produce a description of this type follows from a purely MO element in its construction: the SC orbitals are, in fact, singly-occupied nonorthogonal MOs. The composition of the spin-coupling pattern remains essentially unchanged during the most important part of the 1,3-dipolar cycloaddition process. This suggests that the reacting system remains distinctly nonaromatic before, at, and after the TS. The SC descriptions of the electronic mechanisms of the Diels-Alder reaction between butadiene and ethene and the 1,3-dipolar cycloaddition of fulminic acid to ethyne take theory much beyond the Hückel molecular orbital (HMO) and retricted Hartree-Fock (RHF) levels employed in the formulation of the most popular MO-based treatments of pericyclic reactions, including the Woodward-Hoffmann rules, Fukui's frontier orbital theory and the Dewar-Zimmerman mode. The SC wavefunction maintains near-CASSCF quality throughout the range of reaction coordinate studied for each reaction but, in contrast to its CASSCF counterpart, it is very much easier to interpret and to visualize directly. |
Ab Initio Calculation of NMR Shielding Tensors |
||||
|
Most of the calculations of NMR shielding tensors for larger molecules are still being carried out at a uncorrelated Hartree-Fock (HF) level of theory. However, it is well-known that the accurate ab initio calculation of NMR chemical shielding constants requires inclusion of electron correlation effects. This necessitates the use of post-HF wavefunctions which, taken together with the fact that the elements of the NMR shielding tensor are second-order response properties and their evaluation has to be carried out through an appropriate stationary perturbation theory, suggests that the numerical effort required for calculations of this type should scale very unfavourably with the increase of the size of the molecule.
Since the NMR shielding constants are predominantly local properties, it could be expected that a high-level post-HF description is required only within the close neighborhood of a nucleus of interest, while the remaining, normally much larger, part of the molecule could be described using a simpler and more efficient technique. We have formulated [see P.B. Karadakov and K.Morokuma, Chem. Phys. Lett. 317 (2000) 589] a systematic treatment of this type, which is based on the ONIOM (our own n-layer integrated molecular orbital and molecular mechanics) approach developed by Keiji Morokuma and his group. In the ONIOM approach a molecule is subdivided into n-layers, each of which can be described at a different level of theory. The corresponding NMR shielding tensor represents a combination of the NMR shielding tensors for the different layers. The following two examples use a two-layer ONIOM2(MP2-GIAO:HF-GIAO) variant of this treatment, in which a small part of the molecule containing the nuclei of interest is described at the MP2-GIAO level of theory, and the rest - using the HF-GIAO approach (MP2 stands for second-order Møller-Plesset perturbation theory, and GIAO - for gauge-including atomic orbitals). The results show that with an appropriate partitioining this scheme furnishes shieldings which represent very close approximations to the corresponding MP2-GIAO values for the entire molecule and offers a highly efficient tool for accurate shielding calculations on large molecules. |
||||
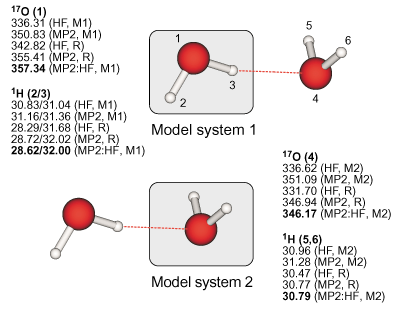 |
Definition of the real and model systems in the case of the water dimer and
results for the 17O and proton absolute isotropic NMR chemical shielding constants. |
|||
|
Definition of the real and model systems for naphthalene and
results for the absolute isotropic NMR chemical shielding constants of the nuclei within the model systems. For further details, see the previous example. |
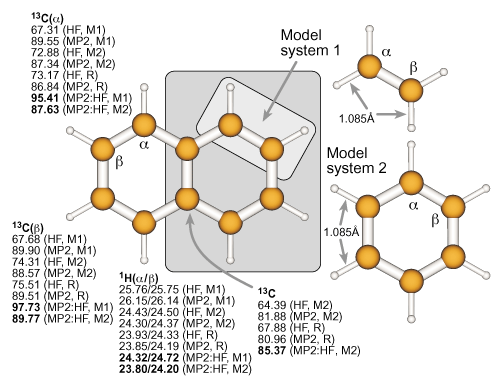 |
Electronic Structure of Extended Systems |
|
In this area, I have been working on the
|
|
Last updated March 2021
|