The Mass of Jupiter

• Learn how to use the Departmental telescope to make visual observations of Solar System objects.
• Learn how to record astronomical images using the CCD camera, specifically of Jupiter and its satellites, and convert these to hard copy.
• Learn how to analyse astronomical images in order to obtain orbital data for the Galilean satellites.
• Learn how to obtain the masses of astronomical objects from their orbital elements.

Hazards and precautions to be taken

The normal hazards and precautions applicable to use of the observatory and its equipment apply. The principal safety rules are as follows:

• The observatory door must be locked to prevent intruder access during observing sessions.
• Care should be taken in the dark in the observatory that wires are not placed in a hazardous position and that backpacks, books or other accessories do not become trip hazards.
• Students should work in pairs in the observatory and ensure that dress is appropriate for cold night observing.
• All observatory rules must be obeyed for safety reasons and usage taught in training adopted.

Please also read the guidelines for safe and correct operation of the telescope, provided after initial training has been completed. To view sections from this handout, click here and press the "back" button in your browser to return to this page.

Introduction

Over half the planets in the solar system have one, or more, natural satellites. Since the motion of these moons is governed by the gravitational properties of the planet, it is possible to determine the mass of the parent planet by observing the motion of its moons. The Galilean moons of Jupiter are easy to observe and provide an ideal example of this technique.

Observations

Use photography or the CCD camera to obtain images of Jupiter* and its moons at accurately known times. Ideally you should obtain a sequence of images of Jupiter's moons that will allow you to determine the orbital period of each of the Galilean satellites. Their periods are such that this will require as many images as practicable at 2 hour intervals for the two inner satellites (Io and Europa) and, for the outer satellites (Ganymede and Callisto), images should be recorded nightly for at least a week. Each group of students should aquire their own data on Io and Europa within a single night. For Ganymede and Callisto, the groups should cooperate to produce as continuous a sequence as possible over a period of one or two weeks.

These observations are dependent on viewing conditions. Should weather make the observations incomplete, a set of specimen data has been provided to allow some reduction of data to give a result. (NB The specimen data was not collected on the telescope you will be using.)

*Jupiter can be located within the night sky by using the 'Cartes du Ciel' sky mapping software, or similar software. This software will tell you where to look for Jupiter as well as giving you a rough guide as to when Jupiter will become visible (i.e. above the horizon). This will aid in planning your time at the observatory most efficently. Should you wish to download this software for your home computer, click here. Otherwise, the software is available on the radio telescope computer in the department, as well as a similar program in the observatory itself.

Data reduction

Having produced hard copies of your images, analyse the data for each of the satellites in turn. Measure the centre to centre distances "r" between the images of Jupiter and, say, Io as accurately as possible. Repeat the process for all four satellites.

Having completed the measurements of r, plot the resulting values against the total time elapsed using the recorded times of each image. Draw a smooth curve through the points and find the maximum distance between Jupiter and the satellite. Choose two points on the curve, one on either side of the maximum, which are near, but not beyond, the ends of the plot. If and are the satellite distances of the selected points, then from figure 1 (shown below) it can be seen that the angles and theta traversed by the satellite to (or from) its greatest elongation point are simply given by;

Calculate the values of the angles to the nearest degree. The total angle traversed by the satellite is then given by;

From your graph, also record the time () taken to move through this angle. Assuming a circular orbit, the sidereal period P is then given by;

Repeat this for all four satellites.

The next problem is to convert the values of from a distance on your image into the real radius of the moon's orbit "a" in kms. This requires the focal length of the telescope "f" and the distance between the earth and Jupiter "D". For the specimen data, D can be taken as 4.46AU and the focal length of the telescope is not needed since there is a 4 arcmin calibration line given.

See figure 2, a diagram showing the necessary information to make this conversion:

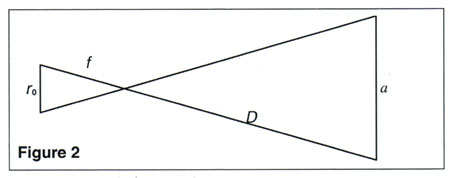
With all the measurements in consistent units of metres;

Calculate "a" for each of the satellites. Plot a graph of "a cubed" versus "P squared", the distance being on the x-axis. By Kepler's laws, this graph should be linear. Get the best straight line fit and find the slope. For a two body problem;

where G is the gravitational constant and the two masses are the masses of the bodies involved. In the case of Jupiter and its moons, the satellite's mass is negligible compared to the mass of Jupiter. Hence, the mass of Jupiter is given by;

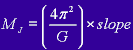
Alternatively, if "a" is measured in AU and "P" in years, then the mass of Jupiter in terms of solar masses is given by;