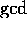 ) between a pair of numbers
) between a pair of numbers 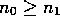 [38]. The algorithm proceeds by calculating the sequence of
divisions with remainder for these numbers:
[38]. The algorithm proceeds by calculating the sequence of
divisions with remainder for these numbers:
Here we describe Euclid's algorithm for finding the greatest
common divisor (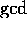 ) between a pair of numbers
) between a pair of numbers 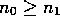 [38]. The algorithm proceeds by calculating the sequence of
divisions with remainder for these numbers:
[38]. The algorithm proceeds by calculating the sequence of
divisions with remainder for these numbers:
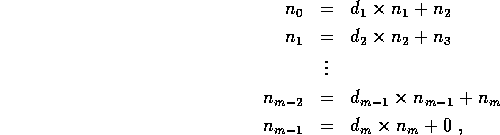
where the 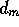 are the quotients and
are the quotients and  at each stage.
The last non-zero remainder
at each stage.
The last non-zero remainder
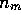 yields the answer, i.e.,
yields the answer, i.e., 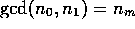 . For example,
the sequence
. For example,
the sequence

shows that  in just two steps. The worst case
number of steps required to complete Euclid's algorithm is
in just two steps. The worst case
number of steps required to complete Euclid's algorithm is
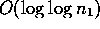 .
.