


Next: Logic gates for
Up: Quantum computation: a tutorial
Previous: Computation without ERASE:
A simple quantum system is the two-level
spin-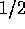 particle. Its basis states, spin-down
particle. Its basis states, spin-down
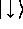 and spin-up
and spin-up 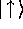 , may
be relabelled to represent binary zero and one, i.e.,
, may
be relabelled to represent binary zero and one, i.e.,
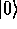 and
and 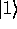 , respectively. The state of a single such
particle is described by the wavefunction
, respectively. The state of a single such
particle is described by the wavefunction
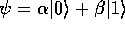 .
The squares of the complex coefficients
.
The squares of the complex coefficients 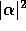 and
and 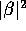 represent the probabilities for finding the particle in the
corresponding states. Generalizing this to a set of k
spin-
represent the probabilities for finding the particle in the
corresponding states. Generalizing this to a set of k
spin-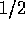 particles we find that there are now
particles we find that there are now 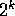 basis states (quantum mechanical vectors that span a Hilbert space)
corresponding say to the
basis states (quantum mechanical vectors that span a Hilbert space)
corresponding say to the  possible bit-strings of length k.
For example,
possible bit-strings of length k.
For example,  is one such state for
k=5.
is one such state for
k=5.
The dimensionality of the Hilbert space grows exponentially with k.
In some very real sense quantum computations make use of this enormous
size latent in even the smallest systems.
Samuel L.~Braunstein
Wed Aug 23 11:54:31 IDT 1995
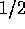 particle. Its basis states, spin-down
particle. Its basis states, spin-down
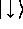 and spin-up
and spin-up 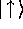 , may
be relabelled to represent binary zero and one, i.e.,
, may
be relabelled to represent binary zero and one, i.e.,
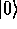 and
and 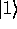 , respectively. The state of a single such
particle is described by the wavefunction
, respectively. The state of a single such
particle is described by the wavefunction
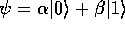 .
The squares of the complex coefficients
.
The squares of the complex coefficients 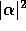 and
and 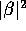 represent the probabilities for finding the particle in the
corresponding states. Generalizing this to a set of k
spin-
represent the probabilities for finding the particle in the
corresponding states. Generalizing this to a set of k
spin-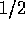 particles we find that there are now
particles we find that there are now 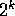 basis states (quantum mechanical vectors that span a Hilbert space)
corresponding say to the
basis states (quantum mechanical vectors that span a Hilbert space)
corresponding say to the  possible bit-strings of length k.
For example,
possible bit-strings of length k.
For example,  is one such state for
k=5.
is one such state for
k=5.