


Next: Quantum parallelism: Period
Up: Quantum computation: a tutorial
Previous: Logic gates for
In this section we describe a simple model for a quantum computer
based on a classical computer instructing a machine to manipulate
a set of spins. This model has some intrinsic limitations which
make designing algorithms in a high-level language somewhat
tricky. We discuss some of the rules for writing such quantum
computer code as a high-level language and give an example.
Consider the following model for the operation of a quantum computer:
Several thousand spin-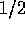 particles (or two-level systems)
are initially in some well defined state, such as spin-down. A classical
machine takes single spins or pairs of spins and entangles them (performing
an elementary one-bit operation
particles (or two-level systems)
are initially in some well defined state, such as spin-down. A classical
machine takes single spins or pairs of spins and entangles them (performing
an elementary one-bit operation 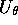 or the two-bit XOR gate); see
Fig. 9a, b and c. These stages are repeated on different
pairs of spins according to the instructions of a conventional computer
program. Since the spins are entangled, we
must not look at the spins at intermediate stages: We must keep the
quantum superposition intact. Furthermore, nothing else may interfere with
the spins which could destroy their orientation or interrupt their unitary
evolution. Once this well-defined cycle of manipulation is complete the
orientations of the spins are measured (Fig. 9d). This set of
measured orientations is the output of the computation.
or the two-bit XOR gate); see
Fig. 9a, b and c. These stages are repeated on different
pairs of spins according to the instructions of a conventional computer
program. Since the spins are entangled, we
must not look at the spins at intermediate stages: We must keep the
quantum superposition intact. Furthermore, nothing else may interfere with
the spins which could destroy their orientation or interrupt their unitary
evolution. Once this well-defined cycle of manipulation is complete the
orientations of the spins are measured (Fig. 9d). This set of
measured orientations is the output of the computation.
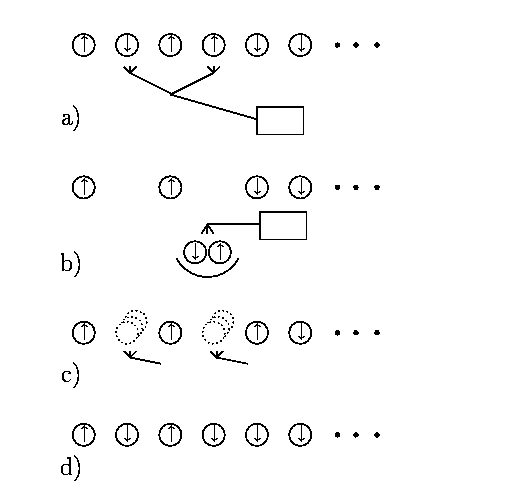
Fig. 9 Model quantum computer as pictured by Shor [21].
Initially all particles are spin-down. Stage a) a classical machine
takes a single or pair of spins and in stage b) it performs a selected
one-bit or two-bit operation; in stage c) the
``entangled'' particles are returned to their original locations.
These three stages are repeated many times in accord with the instructions
given by an ordinary classical computer. When this cycle is complete
stage d) consists of measuring the state of the particles (leaving them
in some particular bit-string); this bit-string is the result of the
computation.
Given this paradigm for a quantum computer, what might its high-level
language (its computer code) look like? The most serious difficulty that
must be dealt with is that the quantum information is manipulated
by a conventional computer in a completely blind manner---without any
access to the values of this quantum information. This means that the
program cannot utilize ``shortcuts'' conditional on the value of a
quantum variable (or register or bit). For example, loops must be iterated
through exactly the same number of times independent of the values of the
quantum variables. Similarly, conditional branches around large pieces of
code must be broken down into repeated conditions for each step. In
addition, each instruction performed upon the quantum bits must be
logically reversible. Thus, ordinary assignments of a value to a
variable, such as
| a = n, are not legal
and must instead be performed as increments on an initially zeroed
variable, such as
| a
= n, are not legal
and must instead be performed as increments on an initially zeroed
variable, such as
| a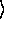 = | a
= | a + n.
+ n.
An example of such code that could run on this machine might look
like this [22]:
do 10 k = 1, worstdiv
| a = | a
= | a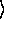 - n
if ( | a
- n
if ( | a >= 0 ) | q
>= 0 ) | q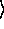 = | q
= | q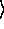 + 1
10 continue
do 20 k = 1, worstdiv
if ( k > | q
+ 1
10 continue
do 20 k = 1, worstdiv
if ( k > | q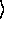 ) | a
) | a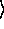 = | a
= | a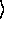 + n
20 continue
+ n
20 continue
This code fragment could be used to calculate the quotient and the
remainder, placed in  and
and  ,
respectively, for the division of
,
respectively, for the division of 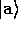 by n; the
constant worstdiv is the worst-case number of times the loop must
be traversed. Here
by n; the
constant worstdiv is the worst-case number of times the loop must
be traversed. Here  is initially zero. Each instruction
here is either a conventional computer instruction or one involving some
quantum variables. The former are direct instructions for the external
computer, while the latter must be interpreted as a sequence of
manipulations to be performed upon the quantum bits. As it stands, this
code is not reversible (neither is it very efficient), e.g., the
label 10 gives no specification of which routes might be used to
get to it. It can, however, be easily rewritten [22].
is initially zero. Each instruction
here is either a conventional computer instruction or one involving some
quantum variables. The former are direct instructions for the external
computer, while the latter must be interpreted as a sequence of
manipulations to be performed upon the quantum bits. As it stands, this
code is not reversible (neither is it very efficient), e.g., the
label 10 gives no specification of which routes might be used to
get to it. It can, however, be easily rewritten [22].



Next: Quantum parallelism: Period
Up: Quantum computation: a tutorial
Previous: Logic gates for
Samuel L.~Braunstein
Wed Aug 23 11:54:31 IDT 1995
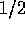 particles (or two-level systems)
are initially in some well defined state, such as spin-down. A classical
machine takes single spins or pairs of spins and entangles them (performing
an elementary one-bit operation
particles (or two-level systems)
are initially in some well defined state, such as spin-down. A classical
machine takes single spins or pairs of spins and entangles them (performing
an elementary one-bit operation 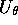 or the two-bit XOR gate); see
Fig. 9a, b and c. These stages are repeated on different
pairs of spins according to the instructions of a conventional computer
program. Since the spins are entangled, we
must not look at the spins at intermediate stages: We must keep the
quantum superposition intact. Furthermore, nothing else may interfere with
the spins which could destroy their orientation or interrupt their unitary
evolution. Once this well-defined cycle of manipulation is complete the
orientations of the spins are measured (Fig. 9d). This set of
measured orientations is the output of the computation.
or the two-bit XOR gate); see
Fig. 9a, b and c. These stages are repeated on different
pairs of spins according to the instructions of a conventional computer
program. Since the spins are entangled, we
must not look at the spins at intermediate stages: We must keep the
quantum superposition intact. Furthermore, nothing else may interfere with
the spins which could destroy their orientation or interrupt their unitary
evolution. Once this well-defined cycle of manipulation is complete the
orientations of the spins are measured (Fig. 9d). This set of
measured orientations is the output of the computation.

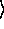 = n, are not legal
and must instead be performed as increments on an initially zeroed
variable, such as
| a
= n, are not legal
and must instead be performed as increments on an initially zeroed
variable, such as
| a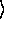 = | a
= | a + n.
+ n.
 = | a
= | a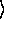 - n
if ( | a
- n
if ( | a >= 0 ) | q
>= 0 ) | q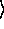 = | q
= | q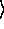 + 1
10 continue
do 20 k = 1, worstdiv
if ( k > | q
+ 1
10 continue
do 20 k = 1, worstdiv
if ( k > | q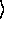 ) | a
) | a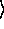 = | a
= | a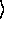 + n
20 continue
+ n
20 continue
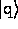 and
and  ,
respectively, for the division of
,
respectively, for the division of 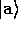 by n; the
constant worstdiv is the worst-case number of times the loop must
be traversed. Here
by n; the
constant worstdiv is the worst-case number of times the loop must
be traversed. Here  is initially zero. Each instruction
here is either a conventional computer instruction or one involving some
quantum variables. The former are direct instructions for the external
computer, while the latter must be interpreted as a sequence of
manipulations to be performed upon the quantum bits. As it stands, this
code is not reversible (neither is it very efficient), e.g., the
label 10 gives no specification of which routes might be used to
get to it. It can, however, be easily rewritten [22].
is initially zero. Each instruction
here is either a conventional computer instruction or one involving some
quantum variables. The former are direct instructions for the external
computer, while the latter must be interpreted as a sequence of
manipulations to be performed upon the quantum bits. As it stands, this
code is not reversible (neither is it very efficient), e.g., the
label 10 gives no specification of which routes might be used to
get to it. It can, however, be easily rewritten [22].