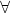 x.
x.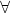 ymarried(x,y)
ymarried(x,y) 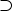 married(y,x)
married(y,x)
[up]
brother/2
First attempt:
brother(X, Y):-
male(X), parent(P, X), parent(P, Y). ?- brother(X,Y). X = harry Y = harry ; X = harry Y = harry ; X = harry Y = wills ; X = harry Y = wills ; X = wills Y = harry ; X = wills Y = harry ; X = wills Y = wills ; X = wills Y = wills ; no |
One problem here is that among the results returned are:
X = harry
Y = harry ; X = wills Y = wills ; |
The first definition of brother/2 is incorrect. It requires an additional condition to the effect that the two individuals must be different:
brother(X, Y):-
male(X), parent(P, X), parent(P, Y), different(X, Y). |
You are not in a position to implement different/2 as yet, because it exceeds the scope of database Prolog. We will return to this at a later date. However, even if this additional condition is included, the results may not be what you expect:
|?-brother(X,Y).
X = harry Y = wills ; X = harry Y = wills ; X = wills Y = harry ; X = wills Y = harry ; no |
The goal returns two sets of identical responses. Why?
son/2
son(X, Y):- male(X), parent(Y, X). |
daughter/2
daughter(X, Y):- female(X), parent(Y, X). |
married/2
|
This needs to be entered as a set of facts. It is not possible to deduce a marriage relationship from any of the other facts in the database.
married(liz, phil).
married(di, chas). |
These facts will provide correct answers to goals matching the facts, but will not produce positive answers to goals such as:
married(phil, liz).
|
One solution to this would be to add this as a new fact. The disadvantage of this strategy is that, for every marriage relationship, we would have to enter two new facts into the database, when there is a generalisation available:
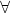 x.
x.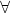 ymarried(x,y)
ymarried(x,y) 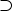 married(y,x)
married(y,x)
’married’ is a symmetrical predicate.
In theory, this translates straightforwardly into Prolog:
married(X, Y):-
married(Y, X). |
Here is the response, given the following facts and rule
married(X, Y):-
married(Y, X). married(liz, phil). married(di, chas). |
to the goal
?- married(liz, X).
ERROR: Out of local stack Exception: (29,563) married(liz, _G158) ? abort % Execution Aborted |
The problem is that the rule calls itself repeatedly, without ever coming up with a solution. Even if the order of facts and goals in the program is reversed, ensuring that at least two solutions are found,
married(liz, phil).
married(di, chas). married(X, Y):- married(Y, X). |
the program will still produced an infinite set of solutions, of which the following are a small subset:
?- married(liz, X).
X = phil ; X = phil ; X = phil ; X = phil ; X = phil ; X = phil ; X = phil |
The moral is that, with respect to symmetrical predicates, logic and Prolog are not equivalent. Prolog is not complete (i.e. it won’t necessarily find all solutions). There is, however, a trick for avoiding this behaviour: to ensure that the rule and the facts do not use the same predicate name:
married_to(liz, phil).
married_to(liz, phil). married(X, Y):- married_to(X,Y). married(X, Y):- married_to(Y,X). ancestor/2 |
For this we need some parent/2 facts:
parent(george_v, george_v1).
parent(george_v1, liz). parent(phil, chas). parent(liz, chas). parent(chas,harry). parent(chas,wills). parent(di,harry). parent(di,wills). |
The starting point is to observe that all parents are ancestors of their children:
ancestor(P, C) :-
parent(P, C). |
We could use this as a model for including the ancestor relationship which exists between grandparents and grandchildren, by including a double call to parent in the body of a second clause for ancestor/2, but this would not be a good move, because there is no limit on the number of generations that can be involved in the ancestor relationship. Instead, the second clause in the definition of the rule should be like this:
ancestor(A, D):-
parent(A, C), ancestor(C, D). |
So, A is D’s ancestor A if has a child (C) who is D’s ancestor.
This definition brings up a very important point: the definition of ancestor refers to itself. It is a
recursive definition.
Solution 2 second/2
second([_, Second|_], Result):-
Result = Second. |
Solution 3 fifth/2
fifth([_, _, _, _, Five|_], Five).
|
The subtle part is to make provision for the list to be of any arbitrary length greater than 5, by using
the Head|Tail notation.
Solution 4 is_list/1
Two clauses, one for the empty list and one for non-empty lists:
is_list([ ]).
is_list([_|_]). |
Solution 5 cons/3
A version with explicit unification:
cons(First, List, Result):-
is_list(List), Result = [First|List]. |
A slightly shorter, but equivalent, version is to ’unfold’ the goal Result = [First|List] and put the relevant unification into the head of the rule, as follows:
cons(First, List, [First|List]):-
is_list(List). |
Solution 6 delete_/3
This, like member/2, can be reduced to the case where the item to be deleted is the head of the list, in which case the third argument simply becomes whatever is left on the list (i.e. its tail):
delete(Item, [Item|Rest], Rest).
|
The recursion deals with those cases where the head of the list is not the item sought. In that case, we disregard it and continue searching the tail of the list. We also need to ensure that the disregarded item is returned as part of the result:
delete(Item, [Head|Tail], Result):-
delete(Item, Tail, InterimResult), Result = [Head|InterimResult]. |
(Again, this can be shortened by unfolding the explicit call to =/2, as follows:
delete(Item, [Head|Tail], [Head|InterimResult]):-
delete(Item, Tail, InterimResult). |
Finally, we need a clause to cover cases where the item sought is not on the list. In that case, the problem reduces to the case where we have reached the end of the list:
delete(Item, [], [ ]).
|
The complete definition is the following three clauses:
delete(Item, [Item|Rest], Rest).
delete(Item, [], [ ]). delete(Item, [Head|Tail], [Head|InterimResult]):- delete(Item, Tail, InterimResult). |
Solution 7 delete_all/3
This is, in fact, just like delete/3, except that the procedure should not halt when the item sought has been found, but should continue to search the remainder of the list. The first clause in delete/3 should therefore be replaced with the following:
delete_all(Item, [Item|Rest], Result):-
delete_all(Item, Tail, Result). |
Note that, on this occasion, the head of the list being searched is ’thrown away’, i.e. not preserved in the third argument (because that is what the goal of delete_all/3 is).
The complete definition is:
delete_all(Item, [ ], [ ]).
delete_all(Item, [Item|Tail], Result):- delete_all(Item, Tail, Result). delete_all(Item, [Head|Tail], [Head|InterimResult]):- delete_all(Item, Tail, InterimResult). |
Solution 8 reverse/2
The base case of this definition is that where the list to be reversed has been exhausted:
reverse([], []).
|
The recursion involves removing the head of the list (i.e. [Head|Tail]), and then continuing to remove the initial item until the list is empty. When that situation is reached, the reduced list is appended (using append/3) to a list consisting only of the removed head. The resulting list (Result) is returned as the value of the top-level call:
reverse([Head|Tail], Result):-
reverse(Tail, Reduced), append(Reduced, [Head], Result). |
Here is a sample trace:
[trace] ?- my_reverse([a,b,c], X).
Call: (7) my_reverse([a, b, c], _G293) ? creep Call: (8) my_reverse([b, c], _G362) ? creep Call: (9) my_reverse([c], _G362) ? creep Call: (10) my_reverse([], _G362) ? creep Exit: (10) my_reverse([], []) ? creep Call: (10) lists:append([], [c], _G369) ? creep Exit: (10) lists:append([], [c], [c]) ? creep Exit: (9) my_reverse([c], [c]) ? creep Call: (9) lists:append([c], [b], _G372) ? creep Call: (10) lists:append([], [b], _G364) ? creep Exit: (10) lists:append([], [b], [b]) ? creep Exit: (9) lists:append([c], [b], [c, b]) ? creep Exit: (8) my_reverse([b, c], [c, b]) ? creep Call: (8) lists:append([c, b], [a], _G293) ? creep Call: (9) lists:append([b], [a], _G370) ? creep Call: (10) lists:append([], [a], _G373) ? creep Exit: (10) lists:append([], [a], [a]) ? creep Exit: (9) lists:append([b], [a], [b, a]) ? creep Exit: (8) lists:append([c, b], [a], [c, b, a]) ? creep Exit: (7) my_reverse([a, b, c], [c, b, a]) ? creep X = [c, b, a] Yes |
Solution 9 translate/2
We need a set of translations, coded here as facts with the predicate translate_word/2. You could have called your version anything you like, and the order of arguments is immaterial.
translate_word('John', 'Jean').
translate_word(is, est). translate_word(an, un). translate_word(idiot, imbecile). |
The actual translation involves the usual recursive predicate, which works its way down the list until it is empty. This gives the base clause:
translate([ ], [ ]).
|
The recursion involves identifying the head of the input list (EH), looking up its translation by a call to translate_word/2. This translation (FH) becomes the head of the output list, while the procedure continues the routine on the remainder of the list (ET).
translate([EH|ET], [FH|FT]):-
translate_word(EH, FH), translate(ET, FT). |
Solution 10 square/2
Easy:
square(N, S):-
S is N*N. |
Solution 11 power/3
This requires 3 clauses:
The zeroth power of any number is 1
power(0, _, 1).
|
The first power of any number is that number itself
power(1, N, N).
|
Subtract one from the power and compute the lower result. The recursion will stop when the Power reaches 1. Then multiply the result of each intermediate calculation by the number whose power is desired
power(Power, Number, Result):-
NextLowerPower is Power - 1, power(NextLowerPower, Number, InterimResult), Result is InterimResult * Number. |
Solution 12 memberchk/2 If both arguments are instantiated, there is no observable difference
between member/2 and memberchk/2
?- member(b, [a,b,c]).
yes ?- memberchk(b, [a,b,c]). yes |
However, if either argument is a variable, memberchk/2 will return only a single result. Once the first clause has succeeded, the cut prevents backtracking to the second clause.
?- memberchk(X, [a,b,c]).
X = a ? ; no ?- memberchk(a, X). X = [a|_A] ? ; no ?- memberchk(X, Y). Y = [X|_A] ? ; no |
Compare the behaviour of member/2 with the same arguments:
?- member(X, [a,b,c]).
X = a ; X = b ; X = c ; No ?- member(a, X). X = [a|_G208] ; X = [_G207, a|_G211] ; X = [_G207, _G210, a|_G214] ; X = [_G207, _G210, _G213, a|_G217] ; X = [_G207, _G210, _G213, _G216, a|_G220] Yes ?- member(X, Y). X = _G157 Y = [_G157|_G229] ; X = _G157 Y = [_G228, _G157|_G232] ; X = _G157 Y = [_G228, _G231, _G157|_G235] ; X = _G157 Y = [_G228, _G231, _G234, _G157|_G238] ; X = _G157 Y = [_G228, _G231, _G234, _G237, _G157|_G241] Yes |
The last two calls would continue to provide alternative results indefinitely.
Solution 13 pred/2
A simulated trace:
[trace] ?- pred(X, [the,talk,of,the,town]).
Call: (7) pred(_G298, [the, talk, of, the, town]) ? creep Call: (8) pred(_G298, [talk, of, the, town]) ? creep Call: (9) pred(_G298, [of, the, town]) ? creep Call: (10) pred(_G298, [the, town]) ? creep Call: (11) pred(_G298, [town]) ? creep Exit: (11) pred(town, [town]) ? creep Exit: (10) pred(town, [the, town]) ? creep Exit: (9) pred(town, [of, the, town]) ? creep Exit: (8) pred(town, [talk, of, the, town]) ? creep Exit: (7) pred(town, [the, talk, of, the, town]) ? creep X = town Yes |
The program takes a list as its second argument and instantiates its first argument to the last item on
the list.
Solution 14 reply/0
reply/0 reads input from the user. If the input is stop, the program terminates; otherwise it processes the input and then calls reply/0 again.
reply:-
read(Input), (Input = stop; process(Input), reply). |
process/1 takes the user’s input, transforms it and then writes the result to the screen.
process(Input):-
change(Input, Output), prettyprint(Output). |
change/2 works its way down the input list, calling swap/2, which makes whatever changes are required.
change([], []).
change([H|T], [NH|R]):- swap(H, NH), change(T, R). |
swap/2 maps input expressions onto output expressions. 'am not' and 'no,' are single-quoted and represented as atoms.
swap(you, i).
swap(french, german). swap(bananas, 'ice cream'). swap(are, 'am not'). swap(do, 'no,'). swap(I, I). |
Finally, prettyprint/1 recursively processes the output, writing the head of the list to the terminal, then a space (enclosed in single quotes, until it reaches the last item on the list, which is written to the screen, followed by a new line.
prettyprint([I]):-
write(I), nl. prettyprint([H|T]):- write(H), write(' '), prettyprint(T). |
[up]