
This page accompanies our "Growing music" EvoMUSART paper, giving some more details, more examples, and MP3 audio samples of the scores. (Click on the scores to hear the music)
All the figures are drawn using the standard turtle graphics rendering:
F : Move forward a length d and draw a line
f : Move forward a length d without drawing a line
+ : Turn left by angle delta
- : Turn right by angle delta
[ : Push current state
] : Pop state
All example L-Systems are from [Prusinkiewicz & Lindenmayer 1990], unless otherwise noted.
F : Play a note
f : Rest
+ : Move up one note in the scale of the chosen key
- : Move down one note in the scale of the chosen key
[ : Push current state
] : Pop state
![[leaf]](pictures/leaf.jpg)
w : X
p1 : X -> F [ + X ] [ - X ] F X
p2 : F -> F F
The score is produced after 5 iterations. This sounds fairly unmusical, since at one point, 9 notes are played simultaneously. Also, there is nothing in the system to change the duration of notes, so the music it makes is rhythmically very dull. The music is ultimately just the leaf laid across the notes in C major.
< : Push everything in the current state except the time
> : Pop everything in the current state except time
S : Play a "slurred" note (consecutives S's are played
together as one long note)
If < > are graphicallyrendered as [ ], and S as F, then the pictures are exactly the same, but the notes in the music are played sequentially.
![[leaf]](pictures/leaf.jpg)
w : X
p1 : X -> S < + X > < - X > S X
p2 : S -> S S
This is a vast improvement. Not only is it rhythmically very interesting but it also makes sense melodically.

w : S
p1 : S -> S S - < - S + S + S > + < + S - S - S >
The first half of the first bar is a distinctive motif that is then repeated transposed a number of times.
Note that the music has been naturally generated in perfect 4/4 time. This is due to there being 8 occurrences of the symbol 'S' in production p1, which represents a specific time period - equal to a double quaver in the examples so far. L-systems with a single rule which has 3 (or a multiple of 3) occurrences of the symbol will fit in 3/4 (or perhaps 3/8) time, and 5 occurrences in 5/4 time and so on.

w : F
p1: F -> F < + F > F < - F > F
Production p1 has 5 occurrences of the symbol representing a period of time. After 2 iterations it produces a melody which fits in 5/8 time
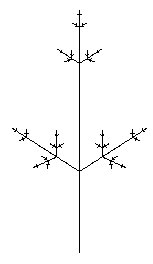
w : X
p1 : X -> S < + X > < - X > S X
p2 : S -> S S S
This distorted leaf no longer creates music that "makes sense": some parts are repeated 6 times, others 9 times and so on. This is generally unmusical.
The seuqntial rendering is musical, but it doesn't capture the ideas of a Schenkerian background/middleground/foreground hierarchy. [Jonas 1972] uses the term "the flowerings of diminution" in describing the sonata form. If we take this analogy literally, an interpretation should be found in which only the ends of the plant (flowers etc) are "heard". The middleground and background (perhaps the trunk and branches in a tree) are not actually heard in Schenkerian analysis - they just give the structure for the foreground to appear from. It seems intuitive that if a plant represents a single melody (part of the foreground), then we are dealing here with the translation of either background or middleground to foreground.
The "Schenkerian" rendering is:
] : play a note
The pitch of the note is still determined by '+' and '-', but the question of the interpretation of 'F' remains. It is clear that this should be something to do with rhythm or the order in which the notes are played.
At first, some L-systems were interpreted with 'F' adding to the time, so that shorter branches are played first followed by longer ones after a period of time proportional to their difference in length. The leaf L-system (from figure 4.2) gives the score in figure 4.7 under this interpretation. There is a period of silence before this starts since the time at which a note is played is dependant on the length of the branch it is associated with, and no branches have length 0, but this silence was removed.
![[leaf]](pictures/leaf.jpg)
w : X
p1 : X -> F [ + X ] [ - X ] F X
p2 : F -> F F
F adds to the time, so that shorter branches are played first followed
by longer ones after a period of time proportional to their difference in
length. 
There is a period of silence before this starts since the time at which a note is played is dependant on the length of the branch it is associated with, and no branches have length 0, but this silence has been removed.
It is better is if the notes are simply played sequentially, as in the
earlier Sequential case. So now ] increments the time (rather than F), and
the time is not pushed and popped with the beginning and end of branches.

This is melodically more pleasing, but the length of branches is being ignored, and there is still no rhythm.
Putting these two ideas together, the number of F's in a branch determines the length of a note, and notes are played sequentially. This is done by incrementing the duration by the initial duration each time an 'F' is encountered when scanning the string, and setting the duration to 0 when a '[' is found (the beginning of a new branch / new note). ']' still pops everything except the time - including the duration - so that the duration of the entire note is proportional to the number of 'F's within the brackets representing that particular branch or note.
F : Increase note duration by initial duration
+ : Move up one note in the scale of the chosen key
- : Move down one note in the scale of the chosen key
[ : Push current state and set note duration to 0
] : Play note according to current state, then pop state
Despite not appearing to fit into a 4/4 framework, this melody sounds very musical, even with a metronome beating 4/4 time behind it.

w : [ F ]
p1 : F -> F F - [ - F + F + F ] + [ + F - F - F ]
Although the production rule for this system produces 8 'F's for each 'F' it encounters in the string, it fits 3/4 time better than the 4/4 time which would be expected.
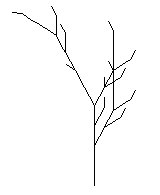
w : [ X ]
p1 : X -> F - [ [ X ] + X ] + F [ + F X ] - X
p2 : F -> F F
This is another example of a score that does not quite fit into any particular time signature but still sounds very musical in an "organic" way.
![[leaf]](pictures/leaf.jpg)
w : X
p1 : X -> F [ + X ] [ - X ] F X
p2 : F -> F F
So far, the L-systems have been evaluated to a depth of 2, 3 or 4 iterations. This is found to be best since there only seems to be enough information in the average L-system to create a short melody and still be interesting. At longer derivations, the melodies begin to get dull, as basically the same bit of music is repeating continually, albeit normally transposed in some way. If the initial duration is adjusted to counter this, the piece becomes far too intricate with unusually short notes.
Use for the L-systems in composition then, appears to be limited to creating small sections of music that could then be used at various points in a complete piece. Alternatively, more than one system could be combined in some way to create something more than just a small fragment of music.
The idea of stochastic systems in generative music is attractive since the same system can be used repeatedly to generate different pieces.
w : F
p1 : F -> F [ + F ] F [ - F ] F : 1
p2 : F -> F [ + F ] F : 1
p3 : F -> F [ - F ] F : 1
These sound random but well structured - not overly complex (as one would expect from the fairly simple nature of the rules). They do sound quite similar to each other, but different enough to be used perhaps at different points in the same piece of music.
Also, reasonably good results are obtained by combining two separate
derivations. One of these starts a fifth above the other and has an
initial duration of twice the length of the other, so that the two
melodies play over each other harmoniously:

The L-systems used in this section are from [Hogeweg & Hesper 1974].
Context sensitivity in L-systems (and grammars) gives more power as parts of the string or plant can grow differently depending on what is around them. This can be useful in music since a generated piece could build to a climax or break down at certain points.
The melodies below generally sound fairly random (despite being deterministic) and are therefore reminiscent of jazz solos. They don't fit well into 4/4 score notation because many of the notes are offbeat, but this just adds to their "freeform" sound. Having said this, the tunes always return to a main motif or phrase that is sometimes transposed or played at a different point in the bar.
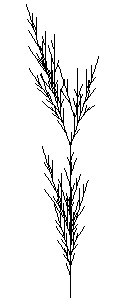
ignore : + - F
w : F 1 F 1 F 1
p1 : 0 < 0 > 0 -> 0
p2 : 0 < 0 > 1 -> 1 [ + F 1 F 1 ]
p3 : 0 < 1 > 0 -> 1
p4 : 0 < 1 > 1 -> 1
p5 : 1 < 0 > 0 -> 0
p6 : 1 < 0 > 1 -> 1 F 1
p7 : 1 < 1 > 0 -> 0
p8 : 1 < 1 > 1 -> 0
p9 : + -> -
p10 : - -> +
The series of notes in the 1st bar is repeated in the 9th bar, but very offbeat (moved forward a quarter of a beat) and raised by 2 semitones. This kind of repetition mirrors how music is normally composed or improvised. The similarity to the pictures generated can be seen in the way that the structures are very complex (appearing random), but recognisable patterns can be seen repeating throughout.

ignore : + - F
w : F 1 F 1 F 1
p1 : 0 < 0 > 0 -> 1
p2 : 0 < 0 > 1 -> 1 [ - F 1 F 1 ]
p3 : 0 < 1 > 0 -> 1
p4 : 0 < 1 > 1 -> 1
p5 : 1 < 0 > 0 -> 0
p6 : 1 < 0 > 1 -> 1 F 1
p7 : 1 < 1 > 0 -> 1
p8 : 1 < 1 > 1 -> 0
p9 : + -> -
p10 : - -> +
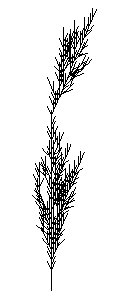
ignore : + - F
w : F 1 F 1 F 1
p1 : 0 < 0 > 0 -> 0
p2 : 0 < 0 > 1 -> 1
p3 : 0 < 1 > 0 -> 0
p4 : 0 < 1 > 1 -> 1 [ + F 1 F 1 ]
p5 : 1 < 0 > 0 -> 0
p6 : 1 < 0 > 1 -> 1 F 1
p7 : 1 < 1 > 0 -> 0
p8 : 1 < 1 > 1 -> 0
p9 : + -> -
p10 : - -> +

ignore : + - F
w : F 0 F 1 F 1
p1 : 0 < 0 > 0 -> 1
p2 : 0 < 0 > 1 -> 0
p3 : 0 < 1 > 0 -> 0
p4 : 0 < 1 > 1 -> 1 F 1
p5 : 1 < 0 > 0 -> 1
p6 : 1 < 0 > 1 -> 1 [ + F 1 F 1 ]
p7 : 1 < 1 > 0 -> 1
p8 : 1 < 1 > 1 -> 0
p9 : + -> -
p10 : - -> +

ignore : + - F
w : F 1 F 1 F 1
p1 : 0 < 0 > 0 -> 0
p2 : 0 < 0 > 1 -> 1 [ - F 1 F 1 ]
p3 : 0 < 1 > 0 -> 1
p4 : 0 < 1 > 1 -> 1
p5 : 1 < 0 > 0 -> 0
p6 : 1 < 0 > 1 -> 1 F 1
p7 : 1 < 1 > 0 -> 1
p8 : 1 < 1 > 1 -> 0
p9 : + -> -
p10 : - -> +
We now adapti previous work in musical formal grammars into an L-system.
If we combine the ideas presented by [Jones 1981] and [Baroni et al 1992], we can write a formal grammar that generates music by recursively splitting up an event space (initially one long note) into 2 or 3 shorter, different notes. After a number of recursions a melody will have been formed which is the length of the initial event space. The insertion rules [Baroni et al 1992] provide tonal information, and the grammar that halves notes can provide the rhythm. Variations of the rules of insertion and the rhythm grammar are given below. The rules of insertion were initially developed for analysis, but adding probabilities as in the stochastic grammar presented by [Jones 1981] allows them to be used for generation. There is an extra insertion rule that does nothing, equivalent to p1 in the Jones grammar.
'd' halves the duration, and 'D' doubles the duration of all subsequent 'F's (we take 'F' to mean play note for now).
Identity : F -> F : 13
Repetition: F -> d F F D : 1
Appogiatura1: F -> d - F + F D : 1
Appogiatura2: F -> d + F - F D : 1
Neighbour note1 : FF -> F d + F - F D : 1
Neighbour note2 : FF -> F d - F + F D : 1
Skip1 : F+F -> F d + + F - F D : 1
Skip2 : F+F -> F d + + + F - - F D : 1
Skip3 : F+F -> F d - F + + F D : 1
Skip4 : F+F -> F d - - F + + + F D : 1
Skip5 : F-F -> - F d + + F - F D : 1
Skip6 : F-F -> - F d + + + F - - F D : 1
Skip7 : F-F -> - F d - F + + F D : 1
Skip8 : F-F -> - F d - - F + + + F D : 1
The axiom can be any desired middleground structure, not just "F". For example, an axiom "F++F++F+F++F" would give a series of notes from the root to the fifth above it. This would then undergo applications of the rules to derive a melody playing around that scale. The stated proportions give notes a 50/50 chance of staying the same or having one of the rules applied to them each time a rule is applied, in reality though these proportions will need to be adjusted to give the optimal or desired complexity.
The rules should be applied in parallel to the whole string to give an even distribution of applications of diminution. In this way, it is already more like an L-system than a formal grammar.
w : F + + F + + F + + + F - - - F - - F - - F (a basic arpeggio)

These work very well as melodies and unsurprisingly sound similar to fragments of the early 20th century European pieces the rules were derived from. In particular, the axiom
w : [---F--F-F-F-F-F-F-F-F-F-F-F][F--F-F-F-F-F-F-F-F-F-F-FF]
taken from the middleground of the first few bars of Debussy's Clair
de lune The
derivations it gives sound similar to the original tune not only in that
they play around the same scale, but also in the style of the melody. This
is a testament to the ability of the rules.
The
derivations it gives sound similar to the original tune not only in that
they play around the same scale, but also in the style of the melody. This
is a testament to the ability of the rules.
The graphical interpretations of these fragments of music are clearly not what we are looking for, however; they look like indistinct scribbles that do not resemble anything in nature except perhaps a coastline. This is due to the edge rewriting fractal way in which they were created.
Using the interpretation with '<' and '>' pushing and popping everything except the time, all the notes are still played sequentially despite the branching.
Identity : F -> F : 13
Repetition : F -> < d F F > : 1
Appogiatura1 : F -> < d - F + F > : 1
Appogiatura2 : F -> < d + F - F > : 1
Neighbour note1 : FF -> < F d + F - F > : 1
Neighbour note2 : FF -> < F d - F + F > : 1
Skip1 : F+F -> < F d + + F - F > : 1
Skip2 : F+F -> < F d + + + F - - F > : 1
Skip3 : F+F -> < F d - F + + F > : 1
Skip4 : F+F -> < F d - - F + + + F > : 1
Skip5 : F-F -> < - F d + + F - F > : 1
Skip6 : F-F -> < - F d + + + F - - F > : 1
Skip7 : F-F -> < - F d - F + + F > : 1
Skip8 : F-F -> < - F d - - F + + + F > : 1
w : F + + F + + F + + + F - - - F - - F - - F
These renderings appear to be branching too much from single points to be comparable to the tree-like structures of most L-systems.
One option in attempting to make the branching more even is to introduce extra random elements into the grammar. If each rule is replaced by two versions of the same rule - one branching off and the other simply continuing along the same branch, then the notes are generated almost exactly as before, but a random branching structure is created.
Identity : F -> F : 26
Repetition: F -> d F F D : 1
Repetition : F -> < d F F > : 1
Appogiatura1: F -> d - F + F D : 1
Appogiatura1 : F -> < d - F + F > : 1
Appogiatura2: F -> d + F - F D : 1
Appogiatura2 : F -> < d + F - F > : 1
Neighbour note1 : FF -> F d + F - F D : 1
Neighbour note1 : FF -> < F d + F - F > : 1
Neighbour note2 : FF -> F d - F + F D : 1
Neighbour note2 : FF -> < F d - F + F > : 1
Skip1 : F+F -> F d + + F - F D : 1
Skip1 : F+F -> < F d + + F - F > : 1
Skip2 : F+F -> F d + + + F - - F D : 1
Skip2 : F+F -> < F d + + + F - - F > : 1
Skip3 : F+F -> F d - F + + F D : 1
Skip3 : F+F -> < F d - F + + F > : 1
Skip4 : F+F -> F d - - F + + + F D : 1
Skip4 : F+F -> < F d - - F + + + F > : 1
Skip5 : F-F -> - F d + + F - F D : 1
Skip5 : F-F -> < - F d + + F - F > : 1
Skip6 : F-F -> - F d + + + F - - F D : 1
Skip6 : F-F -> < - F d + + + F - - F > : 1
Skip7 : F-F -> - F d - F + + F D : 1
Skip7 : F-F -> < - F d - F + + F > : 1
Skip8 : F-F -> - F d - - F + + + F D : 1
Skip8 : F-F -> < - F d - - F + + + F > : 1
w : F + + F + + F + + + F - - - F - - F - - F
This new grammar is a partial success in that the pictures generated by it look vaguely like plants of some kind, and the melodies still sound the same as before. However, it does seem like "cheating" to introduce rules that affect only the graphical interpretation, and not the music.
The L-systems above are able to produce only short melodies. These could be used in combination with each other, and with other fragments of music, to create a piece of music that could be considered whole and complete. An example of such an attempt is given below.
The "Context senstive B" and "context sensitive D" rules (above) are used. Each part is made from various derivations of the systems rearranged, except the chords which were added manually. When they are played with suitable sounds or synthesisers, the result is fairly pleasant (if slightly odd) piece of music. It has melodies playing over a progressive bass line, with pad sounds (sustained notes rather than hit or plucked sounds) providing harmonies.
[Baroni et al 1992]
M Baroni, R Dalmonte, C Jacobini. Theory and Analysis of European
Melody. In Marsdon & Pople, Computer Representations and Models
in Music. Academic Press 1992
[Hogeweg & Hesper 1974]
P Hogeweg, B Hesper. A Model Study On Biomorphological Description.
Pattern Recognition 6:165-179 1974
[Jonas 1972]
O Jonas. Introduction to the Theory of Heinrich Schenker.
Longman, 1972
[Jones 1981]
K Jones. Compositional Applications of Stochastic Processes. Computer
Music Journal 5(2):45-61 1981
[Prusinkiewicz & Lindenmayer 1990]
P Prusinkiewicz, A Lindenmayer. The Algorithmic Beauty Of
Plants. Springer, 1990