home > factoids > superformula

The superformula is a generalisation of the circle, the ellipse, and the superellipse, published by Johan Gielis in 2003.

The equation of a circle of radius $c$ is:

$$x^2 + y^2 = c^2 \mbox{ ; or } \left(\frac{x}{c}\right)^2 + \left(\frac{y}{c}\right)^2 = 1 \mbox{ ; or } r = c$$

where $x = r \sin \phi$ and $y = r \cos \phi$.

The equation of an ellipse with semi-axes $a$ and $b$ is:

$$\left(\frac{x}{a}\right)^2 + \left(\frac{y}{b}\right)^2 = 1 \mbox{ ; or } r = \left[\left(\frac{\cos\phi}{a}\right)^2 + \left(\frac{\sin\phi}{b}\right)^2\right]^{-1/2}$$

The superellipse is a generalisation; the exponents can be any $n$, not just $2$:

$$\left|\frac{x}{a}\right|^n + \left|\frac{y}{b}\right|^n = 1 \mbox{ ; or } r = \left(\left|\frac{\cos\phi}{a}\right|^n + \left|\frac{\sin\phi}{b}\right|^n\right)^{-1/n}$$

Gielis' superformula is a further generalisation, allowing the three occurences of the exponent $n$ to vary independently, and also allowing the frequency of the trigonometric functions to vary:

$$r = \left(\left|\frac{\cos (m\phi/4)}{a}\right|^{n_a} + \left|\frac{\sin (m\phi/4)}{b}\right|^{n_b}\right)^{-1/n}$$

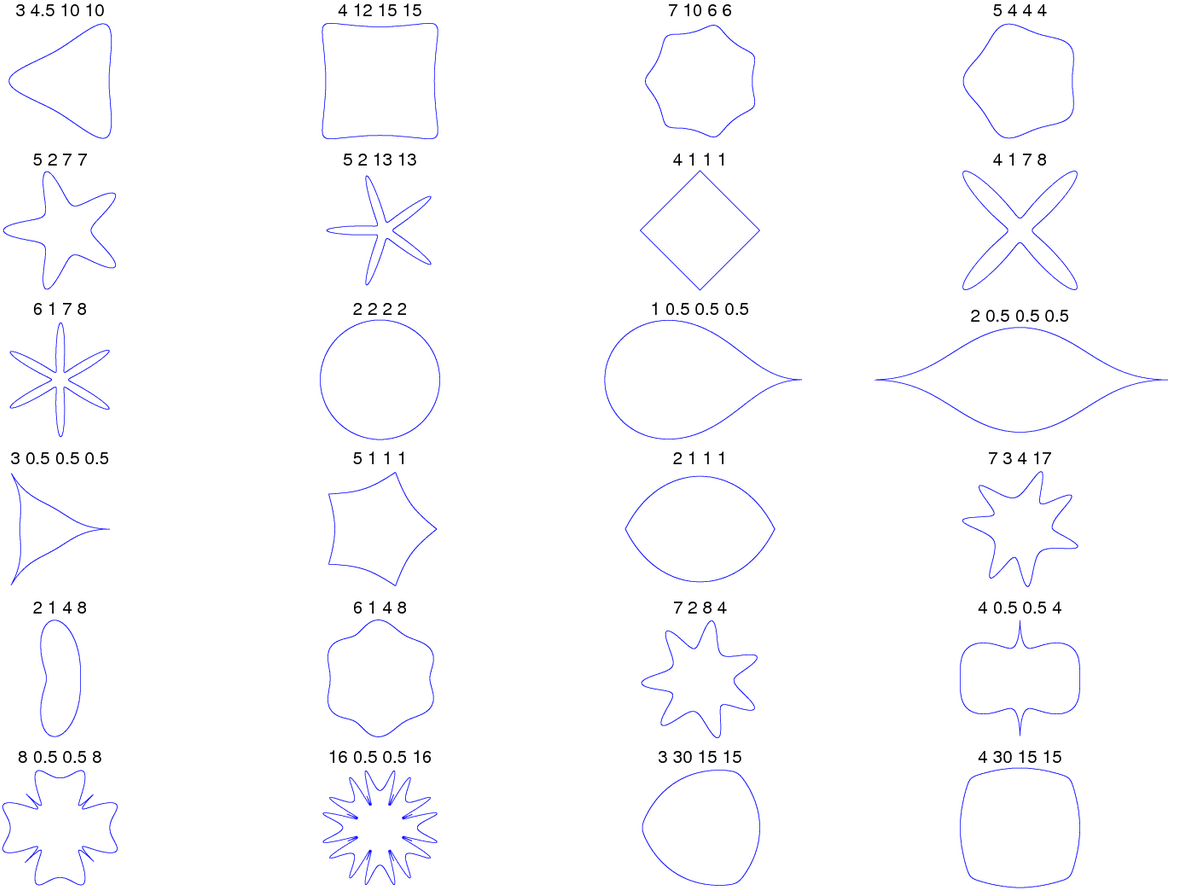
With its many parameters, the superformula can describe a multitude of curves. For example (from the wikipedia superformula page, individual curves labelled by $(m,n,n_a,n_b)$, all with $a=b=1$)

Below is a utility (written in Processing, and using processing.js for execution is a browser). The scrollbars allow variation of $m,n,n_a,n_b,a,b$, plus a further parameter $cy$ described in examples 6,7,8 below. The buttons labelled $0..24$ provide $25$ predefined value sets, displaying a range of possible superformula images. The values of $m$ are restricted to be multiples of $\frac{1}{4}$; the values of $n,n_a,n_b$ are restricted to be multiples of $\frac{1}{2}$.

Predefined images (selected using the numbered buttons):

0. $(4, 2, 2, 2, 1, 1, 1)$ : A circle; $m=4$ removes the frequency change; $n = n_a = n_b = 2$ is the squared exponent; $a = b$ makes it a circle.
1. $(4, 2, 2, 2, 1.8, 0.5, 1)$ : An ellipse; $m=4$ removes the frequency change; $n = n_a = n_b = 2$ is the squared exponent; $a \neq b$ makes it an ellipse rather than a circle.
2. $(4, 3, 3, 3, 1.8, 0.5, 1)$ : A superellipse; $m=4$ removes the frequency change; $n = n_a = n_b \neq 2$ is the non-squared exponent. If $n = n_a = n_b = 1$, the superellipse is a rhombus (see example 16); if $n = n_a = n_b \lt 1$, the sides of superellipse are concave.
3. $(8, 2, 10, 10, 1, 1, 1)$ : An eight-pointed star.
4. $(3, 5, 18, 18, 1, 1, 1)$ : A three-pointed star.
5. $(5, 1, 2, 15, 1, 1, 1)$ : An asymmetric five-pointed star.
6. $(7, 4, 4, 17, 1, 1, 1)$ : An asymmetric seven-pointed star.
7. $(7, 4, 4, 17, 1.3, 1, 1)$ : An asymmetric seven-pointed star with a gap; $a \neq b$. Because $m$ is not an even integer, the frequency term means the value of $r$ is different when $\phi = 0$ and when $\phi = 2\pi$. When $m$ an odd integer, as here, it is easy to show that $r(0) = a^{n_a/n}; r(2\pi)=b^{n_b/n}$. For the curve to join up, we need $a^{n_a/n}=b^{n_b/n}$. One way to achieve this is $a=b=1$ (as in the previous example); another is $a=b\neq 1, n_a=n_b$.
8. $(7, 4, 4, 17, 1.3, 1, 2)$ : An symmetric seven-pointed star with two cycles; $cy = 2$. A further way to make the curve join up for odd $m$ is to plot $\phi$ from $0$ to $4\pi$, or $2$ cycles, $cy = 2$. When $m$ is half-integral, we need $cy=4$; when it is quarter-integral, we need $cy = 8$. Other fractional values (not supported here) would require different values of $cy$; irrational values of $m$ would never join up, no matter how large $cy$.
9. $(12, 15, 20, 3, 1, 1, 1)$ : A fancy dinner plate.
10. $(19, 9, 14, 11, 1, 1, 1)$ : Nineteen spike.
11. $(18, 9, 18, 17, 1, 1.5, 1)$ : Crinkly spikes.
12. $(17.75, 9, 18, 17, 1, 1.5, 8)$ : Crinkly spikey flowerhead; $m=17.75$, so $cy=8$ for a closed curve.
13. $(16, 1, 1, 19, 1, 1, 1)$ : Crinkly, less spikey.
14. $(2, 1, 4, 8, 1, 1, 1)$ : A bean.
15. $(3, 5, 20, 20, 0.7, 1.2, 2)$ : Overlapping trefoils.
16. $(4, 1, 1, 1, 1.5, 1.5, 1)$ : The diamond (rhombus) superellipse; $m=4;$ $n = n_a = n_b = 1$.
17. $(4, 1, 8, 8, 0.9, 0.9, 1)$ : A four-pointed star.
18. $(6, 1, 1, 1, 1.8, 1.1, 1)$ : A lumpy triangle: six-pointed, but very differing sizes.
19. $(10, 1, 1, 1, 1.8, 1.1, 1)$ : A lumpy starfish.
20. $(5, 2, 17, 4, 0.8, 1.5, 2)$ : A five-petalled flower.
21. $(9, 2, 17, 4, 0.8, 1.5, 2)$ : A nine-petalled flower.
22. $(2.5, 0.5, 0.5, 0.5, 2, 2, 2)$ : Rose sepals.
23. $(8, 0.5, 0.5, 8, 1.9, 1.05, 1)$ : A spikey four-leafed clover.
24. $(18, 0.5, 0.5, 4, 1.2, 1.1, 1)$ : A virus.