The Dynamically Variable Digital Waveguide Mesh
Damian Murphy, Simon Shelley, Sten Ternström and David Howard
This companion webpage contains sound
examples in support of the paper "The Dynamically Variable Digital
Waveguide Mesh" by the above authors and presented at the 19th
International Congress on Acoustics, Madrid, 2-7 September 2007.
The sound of this simple dynamic articulation of the 2D vocal tract is available here. Note that the change is smooth and natural sounding. More complex articulation requires more complete control of the vocal tract model itself.
The resulting smooth change in modal frequencies is highlighted in the following spectrogram.
Sound examples for this simulation follow in Table 1 below. Note that with an impulse-like excitation the result is a broad-band noise like impulse response. This can be heard in Membrane_IR (Raw). A low pass filtered version is also included where the change is more clearly evident. Both of these impulse responses are then used to process a simple 'dry' drum loop source.
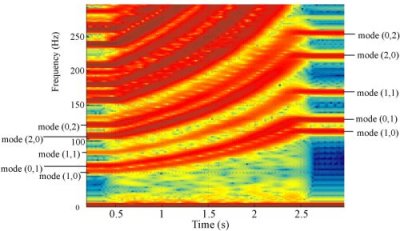
The resulting spectrogram is shown in Fig. 5 below. For the first
20,000 samples the result is that of a normal square mesh, then the
regions or columns of high impedance slowly appear, reaching a
maximum at 60,000 samples. They start to dissapear at 80,000 samples
such that by 120,000 samples they have completely dissapeared,
returning the mesh to its initial shape.
APEX is a tool that can be used to synthesize sound and generate articulatory voice related parameters, based on the positioning of lips, tongue tip, tongue body, jaw opening and larynx height, all mapped from X-ray data. These parameters include vocal tract cross-sectional area function data A(x) as shown in Fig. 7:
The changes in formant pattern from vowel to vowel are clearly evident, with the tract constrictions for /b/ and /d/ being particularly noticeable, demonstrating the potential for high-level synthesis using a dynamically varying DWM. The audio output from this simulation is available here.
dtm, August 2007
Abstract
The digital waveguide mesh (DWM) is a multi-dimensional numerical simulation technique based on the definition of a regular spatial sampling grid for a particular problem domain. This is generally a vibrating object capable of supporting acoustic wave propagation, with the result being sound output for excitation by a given stimulus. To date the output from most DWM based simulations is the static system impulse response for given initial and boundary value conditions. This method is often applied to room acoustics modelling problems, where the offline generation of impulse responses for computationally large or complex systems might be rendered in real-time using convolution based reverberation. More recently, work has explored how the DWM might be extended to allow dynamic variation and the possibility for real-time interactive sound synthesis. This paper introduces the basic DWM model and how the associated algorithms might be extended to include the possibility of allowing dynamic changes as part of the simulation. Example applications that make use of this new dynamic DWM are explored including the synthesis of simple sound objects and the more complex problem of articulatory speech and singing synthesis based on a multi-dimensional simulation of the vocal tract.Examples
The following examples are presented from the results section of the above paper, and demonstrate how the dynamic DWM might be used to synthesize sound. This was first used in our 2D DWM VocalTract work. A good overview is given on the VocalTract page of this site, and includes links to Jack Mullen's Thesis, as well as a version of the software used to generate vocal tract synthesis audio examples and referred to in this paper, which will be available for download from these pages shortly.1. 2D Dynamic Vocal Tract
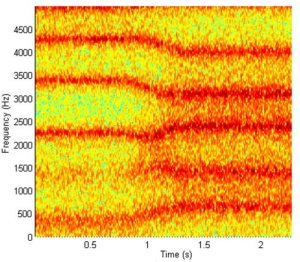
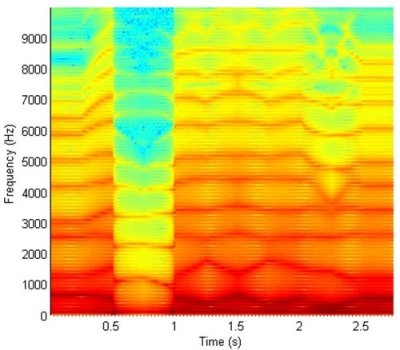
Another example based on Jack's original work in this area and generated using the VocalTract system introduced above, and newly presented for this paper. The spectrogram below shows a smooth interpolation between area function data for the /u/ - ?food?, and /?/ - ?but?, vowels, under noise source excitation, highlighting the resulting change in formant patterns.
Fig 1. Spectrogram
of
a smooth interpolation between area function data for the /u/ -
?food?, and /?/ - ?but?, vowels, under noise source excitation.
The sound of this simple dynamic articulation of the 2D vocal tract is available here. Note that the change is smooth and natural sounding. More complex articulation requires more complete control of the vocal tract model itself.
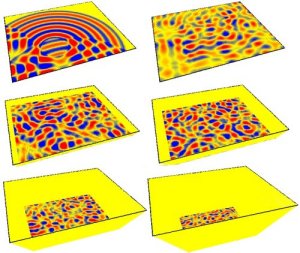
2. 2D Dynamic Shrinking Membrane
In this example a rectangular
membrane of size A (2.86m x 3.3m) is simulated using a 6-port DWM.
Over 80,000 time-steps this membrane is smoothly reduced to one of
size B (1.54m x 1.33m) by increasing the impedance of the mesh from
the outer edge inwards using a linearly varying impedance map. Note
that in the screenshots below the z-axis
denotes increasing impedance.

Fig 2. Mesh
dimensions are altered by linearly increasing the impedance from
the outer edge inwards.
The resulting smooth change in modal frequencies is highlighted in the following spectrogram.

Fig 3. Spectrogram
demonstrating a smooth transition in resonant modes from mesh
size A to mesh size B.
Sound examples for this simulation follow in Table 1 below. Note that with an impulse-like excitation the result is a broad-band noise like impulse response. This can be heard in Membrane_IR (Raw). A low pass filtered version is also included where the change is more clearly evident. Both of these impulse responses are then used to process a simple 'dry' drum loop source.
|
||||||||||
3. 2D Membrane Deformation
In the following example a 2D membrane is deformed by slowly adding and then removing regions of high impedance over the course of a simulation. The impedance map applied is based on a variation of the raised cosine impedance map used in the vocal tract model.
Fig 4. Regions
of high impedance slowly added and then removed over the course of
a simulation.

Fig 5. Spectrogram
of the audio output from a a
square 2D mesh that has smoothly
applied deformations applied to it and then removed.
Sound examples for this simulation follow in Table 2 below. Note
that, as before, with an impulse-like excitation the result is a
broad-band noise like impulse response and this can be heard in
Membrane_IR (Raw). A low pass filtered version is also included where
the change is more clearly evident. These impulse responses are then
used to process a guitar and and an orchestral audio sample.
|
||||||||
4. Articulatory Vocal Tract Speech/Singing Synthesis
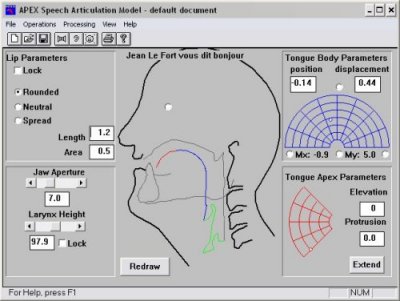
Given the results presented in Example 1 above, the question arises of how a multi-parametric vocal synthesis system based on a 2D DWM might be better articulated to give more natural speech output. Hence the VocalTract system has been further adapted to import A(x) data as a series of text files, with dynamic interpolation from one file to the next allowing more complex articulation than the dipthong synthesis presented in Example 1. The area function information is generated by the APEX Speech Articulation system [1] as shown in Fig. 6 below:
Fig 6. The
APEX system front end.
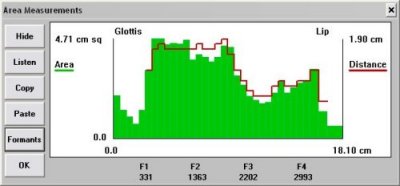
APEX is a tool that can be used to synthesize sound and generate articulatory voice related parameters, based on the positioning of lips, tongue tip, tongue body, jaw opening and larynx height, all mapped from X-ray data. These parameters include vocal tract cross-sectional area function data A(x) as shown in Fig. 7:

Fig 7. A(x)
data generated by the APEX system and used to drive the vocal
tract model.
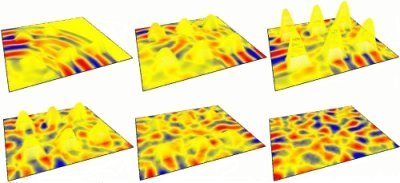
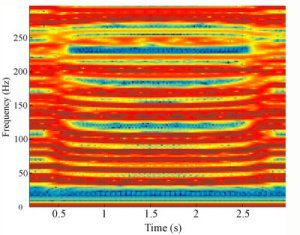
The phrase "A Boy I Adore" is synthesized as a series of nine vocal
tract profiles, /a/ /b/-/O:/-/i/ /a:/-/i/ /a/-/d/-/o/, with a vowel
transition time of 250ms. The results of which are shown in Fig. 8. 
Fig 8. Articulating
the 2-D dynamic DWM vocal tract using the APEX system. The phrase
"A Boy I Adore" is synthesized from nine vocal tract profiles equally spaced in time.
"A Boy I Adore" is synthesized from nine vocal tract profiles equally spaced in time.
The changes in formant pattern from vowel to vowel are clearly evident, with the tract constrictions for /b/ and /d/ being particularly noticeable, demonstrating the potential for high-level synthesis using a dynamically varying DWM. The audio output from this simulation is available here.
References
[1] J. Stark, C. Ericsdotter, P. Branderud, J. Sundberg, H-J. Lundberg and J. Lander, "The APEX model as a tool in the specification of speaker specific articulatory behaviour", Proc. XIVth ICPhS, San Francisco (1999).dtm, August 2007