 d
d
This note describes how to choose the sample size to estimate the 95% limits of aggreement. This approach to the agreement between two method of clinical measurement is described in the paper Statistical methods for assessing agreement between two methods of clinical measurement, Bland JM, Altman DG. (1986). Lancet, i, 307-310.
In our 1986 Lancet paper we gave a formula for the confidence interval for the 95% limits of agreement.
The standard error of the 95% limit of agreement is approximately root( 3 s2/n), where s is the standard deviation of the differences between measurements by the two methods and n is the sample size. The confidence interval is the estimate of the limit, d plus or minus 1.96s, plus or minus 1.96 standard errors.
If you know how accurately you want to estimate the limits of agreement, you can use this to work out the sample size.
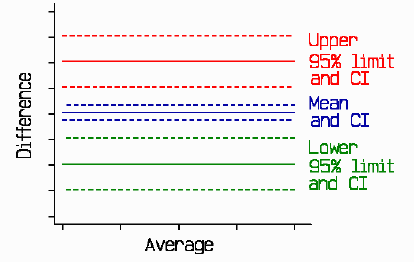
If you think of the 95% CI as +/- 1.96 root(3/n)s, you can see that a sample of 12 gives a 95% CI approximately +/- s. This seems pretty big. If we draw a little picture:
we can see that these confidence intervals are indeed wide. I usually recommend 100 as a good sample size, which gives a 95% CI about +/- 0.34s, which looks something like this:
A sample of 200 subjects is even better, giving a 95% CI about +/- 0.24s. As with all estimation, to determine the appropriate sample size the researcher must decide what accuracy is required.
Back to frequently asked questions on the design and analysis of measurement studies.
Back to measurement studies menu.
Back to Martin Bland's Home Page.
This page maintained by Martin Bland.
Last updated: 12 January, 2004.