29 January 2007
Question
Do you have an approximate date when the Bio-stats assignment results will be out?
Answer
This is a big marking job. It takes me half an hour to mark each one and I have to do this term's teaching at the same time, as well as write papers. Then the marks have to be agreed and feedback sheets prepared. They will not all be finished until, at the least, two weeks from now, i.e. mid-February at the earliest.
15 January 2007
Question
I am calculating RR and OR for the relationship between a diagnosis of high blood pressure and diabetes. I’m having trouble interpreting the output generated from SPSS. The output from SPSS is:
| Value | 95% Confidence Interval | ||
| Lower | Upper | ||
| Odds Ratio for Ever diagnosed with diabetes (no / yes) | 14.125 | 2.143 | 93.084 |
| For cohort Ever diagnosed with high blood pressure = no | 2.260 | .771 | 6.622 |
| For cohort Ever diagnosed with high blood pressure = yes | .160 | .065 | .392 |
| N of Valid Cases | 130 | ||
The odds ratio has been calculated at 14.13. Is the relative risk 2.26 or 0.16?
Answer
This SPSS output is very difficult to understand. I think you need to look at the percentages in the two by two contingency table and see what makes sense.
The online SPSS exercise 'Cough during the day or at night and history of bronchitis, 2' in Week 8 goes through it.
What the second row of the table means is: for a cohort study, the relative risk of NOT having high blood pressure (high blood pressure = no) is 2.260. But I suspect that this means the risk of not high blood pressure in people who do not have diabetes, divided by the risk of not high blood pressure in people who do have diabetes.
To get the relative risk for high blood pressure in diabetes, i.e. the risk of HBP in people with diabetes divided by the risk of HBP in people without diabetes, you will need to recode the two variables to make "no" = 2 intsead of "no" = 0 and make diabetes the row variable. The odds ratio won't be changed, but the relative risk will. The first one will be the one you need.
12 January 2007
Question
In question 4 of the assignment it asks about the relationship of BMI to Age. The natural graphical presentation is a scatterplot. It asks for further statistical analysis. To calculate accurately a regression equation by simple linear regression we have to assume the observations are independent, there is uniform variance, and the deviations have a Normal distribution. This is where it gets difficult, as the BMI and Age both look clearly skewed to me. If this is the case, is it appropriate then and apply simple linear regression?
Answer
I covered this in an answer posted on 8th January as far as correlation goes. Regression, too, is fairly robust and small departures from assumptions do not matter much. It is, of course, the residuals which should have a Normal distribution. I would do the analysis and, if you have any doubts, mention them in your answer.
12 January 2007
Question
How we can calculate the residuals in question 4, because they are needed to check two the of assumptions required to undertake linear regression. Is it necessary for us to do in this assignment? Karen hasn't done that in the exercises.
Answer
This is done in the exercises "Muscle strength, age and height (SPSS exercise)" (Week 9) and "Multiple regression of muscle strength on age and height (SPSS exercise)" (Week 10) on the Applied Biostatistics pages on my website.
12 January 2007
Question
In question 5, which of diabetes or HBP is the exposure and which the event? Are we supposed to report them both ways round?
Answer
The question asks whether they are related, that's all. How you do it up to you, but no direction of causation needs to be assumed.
10 January 2007
Question
How are the marks were allocated for each question? If the total is 100, is it 20 marks for each question or are they weighted to more marks for the more difficult questions?
Answer
We do not give separate marks for each part, but give a mark for the totality of the answer.
10 January 2007
Question
I have assumed that answer to the last question does not require to report RR and OR, because we are supposed to answer exactly what we are asked to avoid negative mark. Would you please tell me if I am right.
Answer
What we said in the notes to the assignment was:
"People do badly in these assignments because they do inappropriate statistics. Read your answers, and determine whether they really answer the question."
and
"People don’t do well in these assignments because they write too much. They worry that they must do the correct thing, and to ensure that they have done the correct thing, they do everything that they can think of. Although this increases the probability that they have done the correct thing, it means that they have certainly done a lot of things which were not correct."
What we were saying is that incorrect analyses will lose marks, not that unnecessary analyses will lose marks.
10 January 2007
Question
When we did linear regression in class we used the example birth weight on gestation time. The intercept was found to be -2.86, we therefore concluded that for the average baby born to a mother with 0 days gestation time the birth weight of the baby would be -2.86kg. In our data of age and BMI, where is the starting point? It cannot be 0 days as in the above example, is it the youngest age in our dataset?
Answer
I don't think we did conclude that, and it is clearly absurd. A baby cannot have negative weight. Such a baby, born at zero weeks, would be a conceptus which did not attach to the wall of the uterus and would be a few cells. The mother would not notice it, but it would have a weight just above zero.
In regression, we should never extrapolate beyond the data. In fact, gestational age curves are usually ogives, flattening toward the axis as age gets closer to zero. In the part of the gestational age range where babies are actually born, a straight line fits the data quite well, well enough for prediction, but it is not the true biological relationship.
The intercept of a regression equation is the value which the y value of the straight line would be when the x value is zero. This is just the same for age and BMI as it is for gestational age and birthweight. Again, we do not extrapolate to babies. All our data are for adults and we would not expect the same straight line to continue into childhood. The intercept determines the vertical positioning of the line and gets it to go through the middle of the data, but it has no physical interpretation in this case.
8 January 2007
Question
In the applied biostats assessment, I'm unclear as to whether our answers need to be a full report with 'introduction, methods, results, discussion and conclusion' as per your notes 'Reporting statistical analyses' or just the 'results' bit of what could be a bigger report.
Answer
In the assignment I wrote:
"Answer each question in the form of a report which could form part of a journal publication. State what method you are using and giving reasons for your choice, give results to an appropriate number of decimal places, and give conclusions based on your analysis."
What I meant was that each answer should be something which would fit into such a report, rather than following the full structure. What we do not want is a chunk of SPSS output.
However, we would have to accept any plausible interpretation of our instructions, so don't worry if you have done something different.
8 January 2007
Question
I have been trying to do a correlation coefficient to look at the relationship between age and BMI. I understand that two assumptions need to be met:
- that the observations are independent and
- at least one of the variables is from a Normal distribution.
Does this mean a perfectly Normal distribution? For age and BMI there is some skew so does this make the P value unreliable?
Also, elsewhere you have said that if the sample is large enough the 'Normal distribution' rule is less significant. Is 143 large enough and does this count for correlation coefficients?
Answer
The assumption of a Normal distribution is required for the P value for the correlation coefficient. As with all such assumptions, some deviation from them is allowable, but the more skew the variables are, the more unreliable the P value becomes. The correlation coefficient is more sensitive to this than are comparisons of means.
Age seldom has a Normal distribution. Why should it? For the whole UK population, the frequency in each each age group is roughly the same up to about 50, where is starts to tail off towards 100. In UK populations BMI is usually positively skew, with a few highly obese people. There are various things we could do to sort this out, but we have not covered them in our brief introduction to statistics. I would suggest reporting the P value and adding a rider that this should be treated with caution due to the distributional problems.
8 January 2007
Question
I have asked SPSS to compute odds ratios and relative risks but the odds ratio is nearly 3 times as large. I have worked it out myself and it is correct but why can this happen? In the lectures the difference has only ever been slight.
Answer
Odds ratio and relative risk are similar when the absolute risks are small. As the absolute risks get bigger, the relative risk gets closer to 1.0 than does the odds ratio.
For example:
| Event | Exposure | |
|---|---|---|
| Yes | No | |
| Yes | 10 | 5 |
| No | 90 | 95 |
| Total | 100 | 100 |
Risks = 0.1 and 0.05, relative risk = 0.1/0.05 = 2.00
Odds ratio = 10 × 95/(5 × 90) = 2.11
| Event | Exposure | |
|---|---|---|
| Yes | No | |
| Yes | 90 | 95 |
| No | 10 | 5 |
| Total | 100 | 100 |
Risks = 0.9 and 0.95, relative risk = 0.9/0.95 = 0.95
Odds ratio = 90 × 5/(95 × 10) = 0.47
| Event | Exposure | |
|---|---|---|
| Yes | No | |
| Yes | 95 | 90 |
| No | 5 | 10 |
| Total | 100 | 100 |
Risks = 0.95 and 0.90, relative risk = 0.95/0.90 = 1.06
Odds ratio = 95 × 10/(90 × 5) = 2.11
In the last one, I have reversed both rows and columns, and I get back to the original odds ratio.
On page 202 of Statistical Questions in Evidence-based Medicine, there is a table with RR = 7 and OR = 94.
4 January 2007
Question
You answered a question about changing the labels on the graphs by going into 'variable view' before making the graph - where is it? I have tried every variation on the tool bar and have got nowhere. I still have not been able to edit the names.
Answer
SPSS has two screen windows, one showing the data spreadsheet and the other the output. On the data spreadsheet window, there are two buttons at the bottom left, one labelled 'Data View' and the other labelled 'Variable View'. Click 'Variable View' and you will see the name, type, label, etc., for each variable. All you need do then is to type whatever you want into the label box for the chosen variable.
4 January 2007
Question
How can I produce separate histograms for male and for female respondents?
Answer
This is an addition to the answer I posted yesterday.
Another way to do this in SPSS, rather than using Data, Split File or Data, Select Cases, is to use the 'Panel by' feature of the Histogram command.
In Graphs, Histogram, put Gender into Columns:. This will give two histograms side by side. Alternatively, put Gender into Rows:. This will give two histograms, one above the other.
3 January 2007
Question
In question 2 of the assessment, do you want the mean and standard deviation for male and females respondants together or seperate as in question 1 with one for male and one for female?
Answer
I meant separately, but I can see that it is not crystal clear.
3 January 2007
Question
In the assignment, do I have to analysis Question 4 using gender as well as age as predictors of BMI?
I think I need to use ANCOVA or something like that. From my results, using General linear regression in SPSS, the effect of gender on BMI was not statistically significant. Is it enough just to mention the results?
Answer
I didn't ask for that. There is no reason why you should not do this if you want to, however.
3 January 2007
Question
How can I produce separate histograms for male and for female respondents?
Answer
In SPSS, you can do this in at least two ways.
You can use Data / Split File / Compare Groups / Gender. This will then give you every graph and analysis command you use for male and female separately.
You can use Data / Select Cases / If condition satisfied / If / Gender = 1 / Continue. This will then give you every graph and analysis command you use for female only. Then change it to gender = 2 and repeat for males only.
3 January 2007
Question
When reporting numerical outcomes in our assignment does it matter if the outcomes are writtten in numerical or word form?
Answer
Write in whatever way you think appropriate.
3 January 2007
Question
I have a problem with interval boundaries. There are two 80 year old women and one 80 year old man in my sample. The histogram of the overall distribution shows 3 people = 80 years:
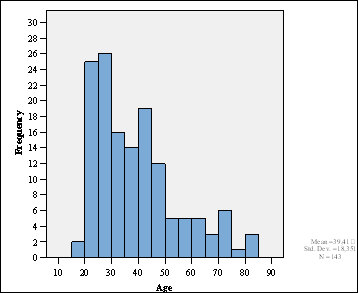
The distribution for female respondents is O.K. (1 female = 80 years):

In male respondents the boundaries seem to be different, although the setting in SPSS is similar.
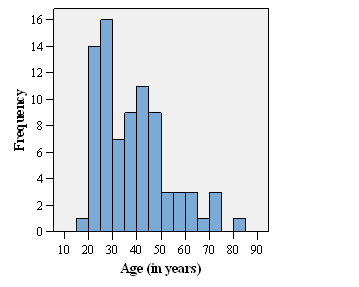
As we can see from the cross-tabulation, there are three aged 80, one female and two males.
| Crosstabs: | ||
| years | female | male |
| . | ||
| . | ||
| 70 | 1 | 3 |
| 71 | 1 | 0 |
| 72 | 1 | 0 |
| 76 | 0 | 1 |
| 80 | 1 | 2 |
Answer
I do not know why SPSS does this. Some histogram programs (or rather histogram programmers) are very uncertain about what happens on the boundary. Stata up to version 8 was the same, though they seem to have fixed it for Stata 9. This is partly because of the way numbers are stored in a computer. 80 might actually be stored as the binary equivalent of 79.99999. This doesn't explain the discrepancy between your histograms and I cannot reproduce it, sorry. The shape of the histogram is what matters of course, rather than the details of each frequency, but I agree that it is very annoying.
3 January 2007
Question
You have indicated in the class that samples greater than 50 follow normal or fairly normal distribution, so examining this matter in the assignment should be unnecessary due to this fact that number of males and females both are more than 50.
Even if we assume that distributions are skew, we are not taught about non-parametric tests. It is indicated in Karen's handout at week 7 that these are outside of scope of this course. Even in handout of week 9, exercise 2, in examining distribution of "gestation time" she neglected an obvious skew, and used Pearson correlation coefficient.
Should we assume a sample with more than 50 members normal without examining (by Q-Q plot or normal histogram)? Is examining necessary, unnecessary, or even has negative mark?
Answer
This is not quite right. I did not say that observations in large samples follow Normal distributions and we have seen many cases where this is not so. What I said was that when comparing two groups we can use the large sample Normal distribution method or z method, even when the observations themselves do not follow a Normal distribution. However, even the large sample Normal test is more powerful when non-Normal observations are transformed to a Normal distribution. Hence it is a good idea to check it. I would certainly not suggest deducting marks for doing this.
This is a short introduction to statistical methods. There was not time to do non-parametric methods. We briefly touched on the use of data transformations to make the distribution more like a Normal distribution before doing a t test.
It is always a good idea to examine the data. It would not carry a negative mark.
14 December 2006
Question
For the assignment, if we delete an outliers from data to show the distribution, should we cut that person out of all our data sets from then on. E.g. in answer to the first question we have a histogram of age for women, but one women is recorded as being 159 years old. Should we include any of her data - e.g. for weight, etc. in any of the analysis afterwards?
Answer
There is no right answer to this. You should do what you think is right, say so, and say why. The most important thing is to state clearly what you have done and why you have done it.
14 December 2006
Question
In SPSS, how do I change legend labels or whatever they are called on the histograms - for example I was going to put age with years in brackets, but nothing I try will let me change axes labels.
Answer
To change the variable label, edit it in Variable View before you create the graph.
14 December 2006
Question
Is there anyway of doing a frequency polygon on SPSS - can't see it.
Answer
I have no idea. I tried to do it but failed. If SPSS can't do it, I doubt that we need it for this assessment.
14 December 2006
Question
I have a different histogram for height, weight and age, for male and female, which seems like a lot, or is that ok?
Answer
If that's what we asked for, that's OK. Don't forget that you have 2000 words, even explaining your thinking and describing and interpeting all the graphs is unlikley to go above that.
27 November 2006
Question
I understand that Fisher's exact test is more appropriate when the sample is not large, however, what percentage of the expected values less than 5 would determine the use of Fisher's Exact test?
Answer
The usual criterion is that to use the chi-squared test 80% of the expected frequencies must exceed five and all must exceed one. Hence for a two by two table, all expected frequencies must exceed five, as if one did not this would leave only 75%. This is only a guide dating from the days when Fisher's exact test was possible only for two by two tables with small frequencies. Fisher's exact test can now be used for any table.
24 November 2006
Question
Although I have a large enough sample for a z-test or chi-squared test, can I use Student's t-test or Fisher's exact test? If I did that, what would be happen?
Answer
You can use Student's t and Fisher's exact test for any sample size. In large samples, you would get the same answers as the z test and chi-squared tests.
In SPSS, there is no separate z test. We have to use the t test with unequal variances, which does the same calculation and gives the same answer. The difference is in the assumptions we must make: for a t test the observations must be from a Normal distribution. We could say that in a two sample t test the assumptions become less and less important as the sample get bigger, until the t test becomes the z test, which has no assumptions about the distribution of the data.
The chi-squared test for association and Fisher's exact test give the same answer for large samples. When the sample is small, Fisher's gives a larger and better P value.
24 November 2006
Question
When I want to see the association between two variables through Linear-by-Linear association, how can I easily discern whether it is positively associated or negatively associated?
Answer
You have to do this by inspecting the row or column percentages. For example, in the exercise we have:
| mothers BMI category before pregnancy * Low birth weight (less than 2.5kg) Crosstabulation | ||||
|---|---|---|---|---|
| Count | ||||
| Low birth weight (less than 2.5kg) | Total | |||
| >=2.5kg | <2.5kg | |||
| mothers BMI category before pregnancy | underweight | 106 | 11 | 117 |
| normal weight | 1122 | 85 | 1207 | |
| overweight | 370 | 19 | 389 | |
| obese | 110 | 4 | 114 | |
| morbidly obese | 46 | 3 | 49 | |
| Total | 1754 | 122 | 1876 | |
The tests give:
chi-squared = 5.56, df=3, P=0.2
linear by linear chi-squared = 4.06, df=1, P=0.04, significant.
If we do the row percentages:
| mothers BMI category before pregnancy * Low birth weight (less than 2.5kg) Crosstabulation | ||||
|---|---|---|---|---|
| Count | ||||
| Low birth weight (less than 2.5kg) | Total | |||
| >=2.5kg | <2.5kg | |||
| mothers BMI category before pregnancy | underweight | 90.6% | 9.4% | 100.0% |
| normal weight | 93.0% | 7.0% | 100.0% | |
| overweight | 95.1% | 4.9% | 100.0% | |
| obese | 96.5% | 3.5% | 100.0% | |
| morbidly obese | 93.9% | 6.1% | 100.0% | |
| Total | 93.5% | 6.5% | 100.0% | |
We can see that the proportion of low birth weight births increases as we go to more obese women, up to the last category. This last category is very small (49 women) and the percentage is unstable. Hence we can see that fatter mothers tend to have bigger babies.
The terms "positive association" and "negative association" were not used in the lecture. Sorry about that. I shall be introducing them in Week 9. However, a positive association is one where large values of one variable are associated with large values of the other variable and a negative association is one where large values of one variable are associated with small values of the other variable. We could say here that low birth weight is negatively associated with weight.
24 November 2006
Question
Among these two tables, which one is better?
A:
| birth weight | baby's ethnic group | |||||
| A | B | C | D | E | F | |
| A | ||||||
| B | ||||||
B:
| baby's ethnic group | birth weight | |
| A | B | |
| A | ||
| B | ||
| C | ||
| D | ||
| E | ||
| F | ||
Answer
I think that B is better, because it fits the page better. Vertical tables are easier to read than horizontal ones.
24 November 2006
Question
The results table of the Chi-squared test gives 1-sided or 2-sided P value or both. Which one should I choose and in which case?
Answer
We only use a 1-sided test for a few very unusual null hypotheses. I have not discussed them in this course. Always use a 2-sided test. I have done only one 1-sided test in my professional career.
24 November 2006
Question
What is the difference between "Asymp. Sig." and "Exact Sig."?
Answer
In SPSS language "Asymp. Sig." ("Asymptotic significance") means the P value for a large sample test based on the Normal or Chi-squared distributions. It is called asymptotic because the distribution of the chi-squared test statistic gets closer and closer to the Chi-squared distribution as samples get larger and larger, but never actually reaches it.
"Exact Sig." means the P value from a test using the individual probabilities of a special discrete distribution, such as the Binomial in the sign test.
In this case "Asymp. Sig." means the P value for the chi-squared test and "Exact Sig." means the P value from Fisher's exact test. (Fisher's exact test uses a distribution called the hypergeometric distribution, which I have no intention of going into!)
21 November 2006
Question
In Exercise 6 of the class on using SPSS in Week 6 we have different degrees of freedom for two groups (equal variances assumed DF = 1993 & equal variances not assumed DF = 718.472). Why do these two groups have different DFs? What does this mean rationally?
Answer
They are not different degrees of freedom for two groups, but different degrees of freedom for two different tests for the difference between the same two groups.
This comes from the mathematics of statistical distributions, which I have spared you in this module.
If we calculate the standard error from a single variance estimate, and so from a single sum of squares about the means, the ratio of difference over standard error will follow the t distribution exactly if the assumptions are met. The degrees of freedom are the degrees of freedom for the sum of squares, the number of observations minus the number of means.
If we calculate the standard error from two different variance estimates, and so from two different sums of squares about the means, the ratio of difference over standard error will NOT follow the t distribution exactly, even if the assumptions are met. So that we could do the test of equality of means without assuming the variance was the same in the two populations, Satterthwaite looked for a replacement for the t distribution, He found that things worked quite well if we replaced the t distribution with the usual degrees of freedom by the t distribution with a smaller number of degrees of freedom.
The Satterthwaite degrees of freedom are NOT the degrees of freedom for the sums of squares, but are approximated by a rather tedious formula involving the two sample sizes and the two variance estimates. This makes the degrees of freedom smaller. When the variances are very different, the degrees of freedom is not much bigger than the degrees of freedom from the more variable sample alone. This makes sense, because in these circumstances the larger variance has much more impact on the standard error than does the smaller variance. Its estimation determines how good the standard error estimate is.
13 November 2006
Question
In question 4 of the exercise "Nurse delivered home exercise programme" in Week 5, it is indicated that "There were 9 serious falls in the control group and 2 in the exercise group, P=0.033".
Are 9 and 2 the mean of serious falling in these groups, or frequencies of serious falling (as it is not indicated)? If they are frequencies, how can we have a P-value?
Answer
They are the numbers of people in the two groups who fell. The authors could compare the proportions falling, using either a chi-squared test or Fisher's exact test, which I shall show you next week. In this case, they used Fisher's exact test.
13 November 2006
Question
In question 3 of classroom exercise week 5, if we compare CIs of two groups we will have an overlap, meaning no significant difference between two groups, but in part b CI of differences excludes 0, meaning significant difference between two groups.
Why this is so? Which one of these method is correct for comparing?
Answer
An overlap in confidence interval does not mean "no significant difference between groups".
It is quite possible for the confidence intervals to overlap and the difference to be significant. Few confidence intervals have the population value at the end of the the interval, so very few pairs of confidence interval for the population value will have the population value in the extremes of both intervals.
In fact, if the null hypothesis were true, for a large sample comparison of two groups, we expect to get a significant difference for 5% of pairs pf samples, but the two confidence intervals would not overlap for only 0.5% of pairs. For 4.5% of pairs, there would be a significant difference but the confidence intervals would overlap.
The confidence interval for the difference would exclude 0 for 5% of samples.
8 November 2006
Question
In the lecture for Week 5, 7 November, there was a difference between standard errors used in significance tests and confidence intervals. Can you explain this?
Answer
I realised while trying to explain it that this point was a point too far for this lecture. However, I started, so I should finish.
I used the example of the difference between two proportions. Now, the variance of the sampling distribution of a proportion is the proportion in the population multiplied by one minus the proportion in the population divided by the number in the sample. It depends on the population proportion itself. The variance of the sampling distribution of the difference between two proportions is the variance of the first proportion plus the variance of the second proportion.
The square root of this variance is the standard error of the difference between two proportions.
In practice, we don't know the proportions in the two populations, so we have to estimate them from the the sample. For the confidence interval, we put the sample proportions into the formula for variance, take the square root, and this gives the estimated standard error. The estimate will be OK provided the sample is large enough.
We could use the same standard error for a significance test. However, if the null hypothesis were true, the two proportions in the populations would be the same. We get a better estimate of what the standard error would be if the null hypothesis were true by using a single sample proportion from a combination of the two groups. We put this into formula for variance in place of each of the population proportions. We use this to test the null hypothesis.
This is why there are two different standard errors and the confidence interval and significance test done using them may give conflicting results.
30 October 2006
Question
In the text version of "Mean and Standard Deviation" at page 6, SD of height data is 2.3 and Variance 39.5. Is this a mistake?
Answer
Yes, it is a mistake. The standard deviation should be 6.3 cm. I have corrected it.
30 October 2006
Question
In the week 4 lecture I can't clearly understand about the concept of 'Number of negatives'.
Is there the concept of 'Number of positives' as well? Can I use the concept of 'Number of positives' instead of that of 'Number of negatives'?
Answer
You can just as well use the number of positives. I think it is easier to see what is going on if we choose the option, positive or negative, which is chosen by the smaller number of people. You should get exactly the same P value.
27 October 2006
Question
During the 2nd lecture the slides were corrected from: “We often divide the distribution into 100 centiles or percentiles” to “We often divide the distribution into 99 centiles or percentiles”.
When centiles split the data into 100 parts why are there only 99 centiles? Is a centile a number (like a quantile) or is it an area?
Answer
A centile is a number. It is a quantile. The first centile cuts off the bottom 1% of the distribution, the second centile cuts off the bottom 2%, and so on. Hence the 99th centile cuts off the bottom 99% of observations. If there were a 100th centile, it would cut off 100%, i.e. it would be a number greater than the maximum possible. There are 99 centiles, just as there are two tertiles, three quartiles, four quintiles, etc. There is one median, which cuts the distribution into two parts.
24 October 2006
Question
In Question 2 in the Week 3 classroom exercise, for the experimental group the mean weight was 71.0 Kg and the SD 23.4 Kg. Does this imply that some people had weight 2 SD's below the mean, that is a weight of 24.8 Kg?
Answer
We expect about 95% of observations to be within two standard deviations of the mean and about 5% to be outside these limits. However, the 5% may all be at one end of the distribution.
For weight we have mean = 71.0 and SD = 23.4.
The 9% range would be
71.0 - 2 × 23.4 = 23.8 to 71.0 + 2 × 23.4 = 117.4.
This is undoubtedly a wide range and the lower limit looks quite low for an adult.
In the 2005 M.Sc. survey, the lowest weight reported was 40.5 Kg and
the highest was 111.4 Kg.
So 117.4 Kg is not an impossible weight.
In old units it is 18 and a half stone.
The mean weight reported in the 2005 survey was 70.1 Kg and the SD 14.7 Kg. The sample in the exercise is much more variable, in both treatment groups. The distribution of weight is usually quite skew to the right, the extreme weights are large weights, as this histogram from the 2005 questionnaire shows:
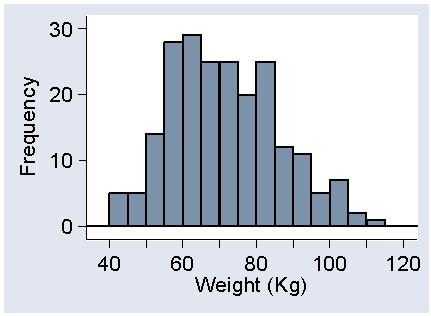
I think that in this small sample of 17 patients there was a very heavy person.