Question 5: Try fitting a curvilinear regression using height only as a predictor. Does there appear to be evidence of a curve rather than a straight line relationship?
We can do this without creating a new variable. SPSS offers a curvilinear regression option to fit curves.
Click Analyze, Regression, Curve Estimation. Select Quadriceps strength into Dependent and Height into Variable. Click Quadratic. (Linear should be checked automatically.) Click OK.
The fourth table of output gives the results:
| Model Summary and Parameter Estimates | ||||||||
|---|---|---|---|---|---|---|---|---|
| Dependent Variable: Quadriceps strength (newtons) | ||||||||
| Equation | Model Summary | Parameter Estimates | ||||||
| R Square | F | df1 | df2 | Sig. | Constant | b1 | b2 | |
| Linear | .176 | 8.321 | 1 | 39 | .006 | -907.626 | 7.203 | |
| Quadratic | .177 | 4.087 | 2 | 38 | .025 | 1693.316 | -23.735 | .092 |
| The independent variable is Height (cm). | ||||||||
The P value attached to the quadratic equation is for the whole model, not for the quadriatic part. For reasons which are not clear to me, to get this we must check the Anova box. If we do this, we get many tables, of which the last is:
| Coefficients | ||||||||
|---|---|---|---|---|---|---|---|---|
| Unstandardized Coefficients | Standardized Coefficients | t | Sig. | |||||
| B | Std. Error | Beta | ||||||
| Height (cm) | -23.735 | 132.719 | -1.382 | -.179 | .859 | |||
| Height (cm) ** 2 | .092 | .394 | 1.801 | .233 | .817 | |||
| (Constant) | 1693.316 | 11164.107 | .152 | .880 | ||||
"Height (cm) ** 2" is computerese for "height squared".
Now we can see that the quadratic term is not significant, P = 0.8, so there is little or no evidence for a curve.
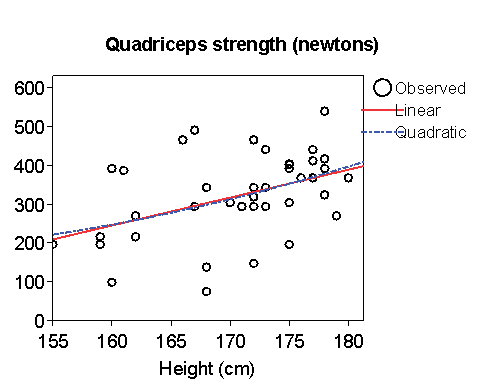
The program also prints a scatter diagram with the straight line and quadratic curve shown. (As usual, I have edited it for legibility on a web page.)

The straight line and the curve are almost identical, which is consistent with the quadratic term being not significant.
Back to Exercise: Multiple regression of muscle strength on age and height.
To Applied Biostatistics index.
To Martin Bland's M.Sc. index.
This page maintained by Martin Bland.
Last updated: 18 December, 2006.