D
This lecture is based on Bland JM, Altman DG (1986) Statistical methods for assessing agreement between two methods of clinical measurement. Lancet i, 307-310.
Clinicians often wish to have data on, for example, cardiac stroke volume or blood pressure where direct measurement without adverse effects is difficult or impossible. The true values remain unknown. Instead indirect methods are used, and a new method has to be evaluated by comparison with an established technique rather than with the true quantity. If the new method agrees sufficiently well with the old, the old may be replaced. This is very different from calibration, where known quantities are measured by a new method and the result compared with the true value or with measurements made by a highly accurate method. When two methods are compared neither provides an unequivocally correct measurement, so we try to assess the degree of agreement. I shall describe the limits of agreement approach to this, also known as the Bland Altman method (Altman and Bland 1983, Bland and Altman 1986).
Most of the analysis will be illustrated by a set of data (Table 1) collected to compare two methods of measuring peak expiratory flow rate (PEFR).
| Subject | Wright peak flow meter | Mini Wright peak flow meter | ||
|---|---|---|---|---|
| First PEFR (l/min) | Second PEFR (l/min) | First PEFR (l/min) | Second PEFR (l/min) | |
| 1 | 494 | 490 | 512 | 525 |
| 2 | 395 | 397 | 430 | 415 |
| 3 | 516 | 512 | 520 | 508 |
| 4 | 434 | 401 | 428 | 444 |
| 5 | 476 | 470 | 500 | 500 |
| 6 | 557 | 611 | 600 | 625 |
| 7 | 413 | 415 | 364 | 460 |
| 8 | 442 | 431 | 380 | 390 |
| 9 | 650 | 638 | 658 | 642 |
| 10 | 433 | 429 | 445 | 432 |
| 11 | 417 | 420 | 432 | 420 |
| 12 | 656 | 633 | 626 | 605 |
| 13 | 267 | 275 | 260 | 227 |
| 14 | 478 | 492 | 477 | 467 |
| 15 | 178 | 165 | 259 | 268 |
| 16 | 423 | 372 | 350 | 370 |
| 17 | 427 | 421 | 451 | 443 |
The sample comprised colleagues and family, chosen to give a wide range of PEFR but in no way representative of any defined population. Two measurements were made with a Wright peak flow meter and two with a mini Wright meter, in random order. All measurements were taken by the same observer, using the same two instruments. (These data were collected to demonstrate the statistical method and provide no evidence on the comparability of these two instruments.) We did not repeat suspect readings and took a single reading as our measurement of PEFR. Only the first measurement by each method is used to illustrate the comparison of methods, the second measurement being used in the study of repeatability.
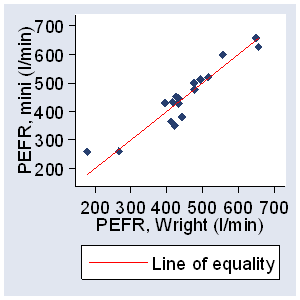
The first step is to plot the data and draw the line of equality on which all points would lie if the two meters gave exactly the same reading every time (Figure 1).
Figure 1. PEFR measured with large Wright peak flow meter and mini Wright peak flow meter, with line of equality
This helps the eye in gauging the degree of agreement between measurements, though, as we shall see, another type of plot is more informative.
It is most unlikely that different methods will agree exactly, by giving the identical result for all individuals. We want to know by how much the new method is likely to differ from the old: if this is not enough to cause problems in clinical interpretation we can replace the old method by the new or use the two interchangeably. If the two PEFR meters were unlikely to give readings which differed by more than, say, 10 l/min, we could replace the large meter by the mini meter because so small a difference would not affect decisions on patient management. On the other hand, if the meters could differ by 100 l/min, the mini meter would be unlikely to be satisfactory. How far apart measurements can be without causing difficulties will be a question of judgment. Ideally, it should be defined in advance to help in the interpretation of the method comparison and to choose the sample size.
The first step is to examine the data. A simple plot of the results of one method against those of the other (Figure 1), though without a regression line, is a useful start. I have tried to get the scales the same so that the two measurements will be shown in the same way. The line in Figure 1 is the line of equality, which points would lie on if agreement were perfect. Usually the data points will be clustered near this line and it will be difficult to assess between-method differences. A plot of the difference between the methods against their mean may be more informative. Figure 2 displays considerable lack of agreement between the large and mini meters, with discrepancies of up to 80 l/min.
Figure 2. Difference against mean for PEFR data
These differences are not obvious from Figure 1. Again, I have tried to get the vertical an horizontal scales to be the same, so that we get a good visual impression of the agreement, or lack of it. The plot of difference against mean also allows us to investigate any possible relationship between the measurement error and the true value. We do not know the true value, and the mean of the two measurements is the best estimate we have.
It would be a mistake to plot the difference against either value separately because the difference will be related to each, a well-known statistical artefact (Gill et al., 1985).
For the PEFR data, there is no obvious relation between the difference and the mean.
Under these circumstances we can summarise the lack of agreement by calculating the bias,
estimated by the mean difference 
and the standard deviation of the differences (s).
If there is a consistent bias we can adjust for it by subtracting
from the new method.
For the PEFR data the mean difference (large meter minus small meter)
is –2.1 l/min and s is 38.8 l/min.
We would expect most of the differences to lie between
– 2s
and + 2s
(Figure 3).
Figure 3. Difference against mean for PEFR data, with mean difference and mean ± 2SD marked
If the differences follow a Normal (Gaussian) distribution,
95% of differences will lie between these limits (or, more precisely, between
– 1.96s
and + 1.96s).
Such differences are likely to follow a Normal distribution because
we have removed a lot of the variation between subjects
and are left with the measurement error.
The measurements themselves do not have to follow a Normal distribution,
and often they will not.
We can check the distribution of the differences by drawing a histogram, as in Figure 4.
Figure 4. Histogram of differences for PEFR data
If this distribution is skewed or has very long tails the assumption of a Normal distribution may not be valid (see below).
Provided differences within ± 2s
would not be clinically important, we could use the two measurement methods interchangeably.
We shall refer to these as the "limits of agreement".
For the PEFR data we get:
– 2s
= –2.1 – 2×38.8 = –79.7 l/min
+ 2s
= –2.1 + 2×38.8 = 75.5 l/min
Thus, the mini meter may be 80 l/min below or 76 l/min above the large meter, which would be unacceptable for clinical purposes. This lack of agreement is by no means obvious in Figure 1.
I don't like to boast, but I have to tell you this, as you will see it in the literature, Figure 3 is called a Bland Altman plot and the limits of agreement method is often called the method of Bland and Altman!
The limits of agreement are only estimates of the values which apply to the whole population. A second sample would give different limits. We can calculate standard errors and confidence intervals to see how precise our estimates are, provided the differences follow a distribution which is approximately Normal. The method is as follows, but the details are not necessary for the course, only the principle that we can and should calculate the confidence interval.
The standard error of
is √(s2/n),
where n is the sample size, and the standard error of
– 2s and
+ 2s is about
√(3s2/n).
95% confidence intervals can be calculated by finding the appropriate point
of the t distribution with n – 1 degrees of freedom,
on most tables the columns marked 5% or 0.05, and then the confidence interval
will be from the observed value minus t standard errors
to the observed value plus t standard errors.
For the PEFR data, s = 38.8.
The standard error of is thus 9.4 l/min.
For the 95% confidence interval we have 16 degrees of freedom and t = 2.12.
Hence the 95% confidence interval for the bias is –2.1 – 2.12×9.4 to
–2.1 + 2.12×9.4, giving –22.0 to 17.8 l/min.
The standard error of the limit
– 2s is 16.3 l/min.
The 95% confidence interval for the lower limit of agreement is –79.7 – 2.12×16.3
to –79.7 + 2.12×16.3, giving –114.3 to –45.1 l/min.
For the upper limit of agreement the 95% confidence interval is 40.9 to 110.1 l/min.
These intervals are wide, reflecting the small sample size
and the great variation of the differences.
They show, however, that even on the most optimistic interpretation
there can be considerable discrepancies between the two meters and
that the degree of agreement is not acceptable.
Figure 5 shows a comparison of oxygen saturation measured by an oxygen saturation monitor and pulsed oximeter saturation, a new non-invasive technique (Tytler and Seeley 1986).
Figure5. Oxygen saturation monitor and pulsed saturation oximeter
Here the mean difference is 0.42 percentage points with 95% confidence interval 0.13 to 0.70. Thus pulsed oximeter saturation tends to give a lower reading, by between 0.13 and 0.70. Despite this, the limits of agreement (–2.0 and 2.8) are small enough for us to be confident that the new method can be used in place of the old for clinical purposes.
This was the first real application I did. Note that I did not make the scales comparable, a mistake.
In the preceding analysis it was assumed that the differences did not vary in any systematic way over the range of measurement. This may not be so. Figure 6 compares the measurement of mean velocity of circumferential fibre shortening (VCF) by the long axis and short axis in M-mode echocardiography (D'Arbela et al., 1986).
Figure 6. Mean VCF by long and short axis measurements
Once more, I did not equalise the scales in these early studies. The scatter of the differences increases as the VCF increases. We could ignore this, but the limits of agreement would be wider apart than necessary for small VCF and narrower than they should be for large VCF. If the differences are proportional to the mean, a logarithmic transformation should yield a picture more like that of Figures 2 and 4, and we can then apply the analysis described above to the transformed data.
Figure 7 shows the log-transformed data of Figure 6.
Figure 7. Data of Figure 6 after logarithmic transformation
This still shows a relation between the difference and the mean VCF, but there is some improvement. The mean difference is 0.003 on the log scale and the limits of agreement are –0.098 and 0.106. However, although there is only negligible bias, the limits of agreement have somehow to be related to the original scale of measurement. If we take the antilogs of these limits, we get 0.80 and 1.27. However, the antilog of the difference between two values on a log scale is a dimensionless ratio. The limits tell us that for about 95% of cases the short axis measurement of VCF will be between 0.80 and 1.27 times the long axis VCF. Thus the short axis measurement may differ from the long axis measurement by 20% below to 27% above. (The log transformation is the only transformation giving back-transformed differences which are easy to interpret, and we do not recommend the use of any other in this context.)
Sometimes the relation between difference and mean is more complex than that shown in Figure 6 and log transformation does not work. Here a plot in the style of Figure 2 is very helpful in comparing the methods. Formal analysis, as described above, will tend to give limits of agreement which are too far apart rather than too close, and so should not lead to the acceptance of poor methods of measurement. But see Bland and Altman (1999) for more advanced methods.
Two widely used approaches which can be misleading are correlation coefficients and regression slopes and intercepts. Correlation is particularly widely used. As for measurement error, correlation coefficients depend on the spread of the data and hence on the sampling. This means that we should only use them when we have a representative sample. But the main problem is that they totally ignore bias. For example, for the PEFR measurements, the correlation between the Wright meter and Mini meter measurements is r = 0.94. If we add 100 to all our PEFR measures made using the Mini meter, to create a systematic bias, the correlation is still r = 0.94 (Figure 8).
Figure 8. Effect on the correlation coefficient of systematic bias
For a description of the problems see Bland and Altman (2003).
Repeatability is relevant to the study of method comparison because the repeatabilities of the two methods of measurement limit the amount of agreement which is possible. If one method has poor repeatability — i.e. there is considerable variation in repeated measurements on the same subject — the agreement between the two methods is bound to be poor, too. When the old method is the more variable one, even a new method which is perfect will not agree with it. If both methods have poor repeatability, the problem is even worse.
As we saw in Week 1, the best way to examine repeatability is to take repeated measurements on a series of subjects. Table 1 shows paired data for PEFR. We can plot a figure similar to Figure 2, showing differences against mean for each subject.
Figure 9 shows the plot for pairs of measurements made with the mini Wright peak flow meter.
Figure 9. Repeated measures of PEFR using mini Wright peak flow meter
There does not appear to be any relation between the difference and the size of the PEFR. There is, however, a clear outlier. I have retained this measurement for the analysis, although I suspect that it was technically unsatisfactory.
We then calculate the mean and standard deviation of the differences as before. The mean difference should here be zero since the same method was used. (If the mean difference is significantly different from zero, we will not be able to use the data to assess repeatability because either knowledge of the first measurement is affecting the second or the process of measurement is altering the quantity.) For the PEFR by the mini meter, the standard deviation of differences between the 17 pairs of repeated measurements is 28.2 l/min.
We expect 95% of differences to be less than two standard deviations. Now, this is the standard deviation of the difference between two measurements on the same person. It is equal to √2 times the within subjects standard deviation, sw. Hence this is the repeatability coefficient of Week 1. For the mini meter, the coefficient of repeatability is twice the standard deviation of the differences, or 56.4 l/min. For the large meter the coefficient is 43.2 l/min.
Compare these repeatability coefficients to the limits of agreement, –80 l/min to +76 l/min. We estimate that the mini meter will be within 56 l/min of another measurement by itself, but only within 80 l/min of a measurement by the Wright peak flow meter. We can conclude that not all the variation between the two instruments is because of their measurement error, but there is some other source of variation.
Altman DG, Bland JM. Measurement in medicine: the analysis of method comparison studies. The Statistician 1983; 32, 307-317.
Bland JM, Altman DG. (1986). Statistical methods for assessing agreement between two methods of clinical measurement. Lancet, i, 307-310.
Bland JM, Altman DG. (1999) Measuring agreement in method comparison studies. Statistical Methods in Medical Research 8, 135-160.
Bland JM and Altman DG. (2003) Applying the right statistics: analyses of measurement studies. Ultrasound in Obstetrics and Gynecology, 22, 85-93.
D'Arbela PG, Silayan ZM, Bland JM. Comparability of M-mode echocardiographic long axis and short axis left ventricular function derivatives. British Heart Journal 1986; 56: 445-9.
Gill JS, Zezulka AV, Beevers DG, Davies P. Relationship between initial blood pressure and its fall with treatment. Lancet 1985; i: 567-69.
Tytler JA, Seeley HF. The Nellcor N-101 pulse oximeter - a clinical-evaluation in anaesthesia and intensive-care. Anaesthesia 1986; 41: 302-305.
To Measurement in Health and Disease index.
To Martin Bland's M.Sc. index.
This page maintained by Martin Bland.
Last updated: 30 May, 2008.
