 D
D
Sometimes we have several outcome variables and we are interested in the effect of treatment on all of them. For example, Motallebzadeh et al. (2007) compared the neurocognitive function of 212 coronary artery bypass surgery patients who were randomised to have the procedure on-pump, i.e. an artificial pump took over the function of the heart, or off-pump, where the heart continued to function. An observational study had suggested that using the pump resulted in long-term damage to neurocognitive function. The patients did a battery of tests which produced 21 different outcome variables. If we compared each of these between the treatment groups, each individual variable would include only a small part of the information, so power would be reduced. Also, the possibility of a Type I error, where we have a significant difference in the sample but no real difference in the population, would be increased. We could deal with the type I error by the Bonferroni correction, multiplying each P value by 21, but this would reduce the power further.
The approach used by Motallebzadeh et al. (2007) was to find a combination of the 21 variables which contained as much of the available information as possible. This was done using a method called principal component analysis or PCA. This finds a new set of variables, each of which is a linear combination of the original variables. A linear combination is found by multiplying each variable by a constant coefficient and adding, as in a multiple regression equation. In PCA, we make the sum of the coefficients squared equal to one. This is an arbitrary method of enabling us to assign numerical values to the components. First we find the linear combination which has the greatest possible variance. We call this the first principal component. We then consider all the possible linear combinations which are not correlated with the first component and find the one with the largest variance. This combination is the second principal component. We then consider all the possible linear combinations which are not correlated with either the first or the second principal component and find the one with the largest variance. This combination is the third principal component. We can go on like this until we have as many principal components as there are variables. The advantage that the principal components have over the original variables is that they are all uncorrelated and that they are ordered by how much variance they have, how much information they contain.
These calculations are all done by computer programs and the mathematics is all done using matrix algebra. We will omit this and go straight to the computer output (in this case from Stata). Table 1 shows the eigenvalues of the principal components.
| Component | Eigenvalue | Percentage of variability explained | Cumulative percentage of variability |
|---|---|---|---|
| 1 | 8.35 | 39.8 | 39.8 |
| 2 | 2.39 | 11.4 | 51.2 |
| 3 | 1.82 | 8.7 | 59.8 |
| 4 | 1.17 | 5.6 | 65.4 |
| 5 | 1.05 | 5.0 | 70.4 |
| 6 | 0.88 | 4.2 | 74.6 |
| 7 | 0.76 | 3.6 | 78.2 |
| 8 | 0.70 | 3.3 | 81.6 |
| 9 | 0.67 | 3.2 | 84.8 |
| 10 | 0.47 | 2.2 | 87.0 |
| 11 | 0.42 | 2.0 | 89.0 |
| 12 | 0.39 | 1.9 | 90.9 |
| 13 | 0.34 | 1.6 | 92.5 |
| 14 | 0.31 | 1.5 | 93.9 |
| 15 | 0.26 | 1.2 | 95.2 |
| 16 | 0.25 | 1.2 | 96.3 |
| 17 | 0.21 | 1.0 | 97.4 |
| 18 | 0.20 | 1.0 | 98.3 |
| 19 | 0.18 | 0.8 | 99.2 |
| 20 | 0.14 | 0.7 | 99.8 |
| 21 | 0.03 | 0.2 | 100.0 |
| Total | 21.00 | 100.0 |
Eigenvalues are a mathematical construct much used in matrix algebra and in the study of linear transformation. (‘Eigen’ is German for ‘own’.) As far as we are concerned it is just a name for something which tells us how variable the principal components are. The column of eigenvalues adds to 21, the number of variables. The variances of the principal components are equal to the eigenvalues. Hence the eigenvalue divided by the sum of all the eigenvalues is the proportion of the total amount of variance which that component represents. In Table 1, this is shown in the column headed ‘Proportion’. We can see that our first principle component has eigenvalue 8.35196 and 8.35196/21 = 0.3977. Hence our first principal component includes a proportion 0.3977, or 40%, of the total variation of all the 21 variables. The second principle component contains a further 0.1140, or 11% of the total variance, and so on. For this study, we just used the first principal component as our outcome variable.
Table 2 shows the coefficients for the first principal component.
| Variable | Component 1 |
|---|---|
| cft | 0.03347 |
| cft1 | 0.24594 |
| cft2 | 0.24818 |
| gpt | –0.19108 |
| gpt1 | –0.16609 |
| ravlt_1 | 0.22261 |
| ravlt_2 | 0.23434 |
| ravlt_3 | 0.27129 |
| ravlt_4 | 0.27177 |
| ravlt_5 | 0.25437 |
| ravlt_b | 0.15745 |
| ravlt_6 | 0.25408 |
| ravlt_30min | 0.25588 |
| lct | –0.16818 |
| lct1 | –0.14615 |
| tmt | –0.19957 |
| tmt1 | –0.25476 |
| sdrt | –0.25251 |
| vft | 0.20014 |
| vft1 | 0.19292 |
| vft2 | 0.21412 |
If we square these coefficients and add them, we get 1.00. Table 2 enables us to calculate the first principal component for each subject. We standardise each variable (i.e. subtract the mean and divide by the standard deviation), multiply each by the coefficient, and add. The program would do this for us directly, but having the coefficients meant that we could calculate it for the same variables measured after surgery and at the three and six months follow-up. (The result was that there was indeed a reduction in test score after surgery for on-pump patients, but this was entirely recovered after six months.)
The reason a single linear combination of the 21 variables can include 39.8% of the variation is that many of these neurocognitive test outcomes are correlated with one another. Compare Table 3, which shows the result of a simulation, where PCA was done using 21 randomly generated Normal variables for 200 subjects.
| Component | Eigenvalue | Percentage of variability explained | Cumulative percentage of variability |
|---|---|---|---|
| 1 | 1.64 | 7.8 | 7.8 |
| 2 | 1.52 | 7.2 | 15.0 |
| 3 | 1.42 | 6.8 | 21.8 |
| 4 | 1.32 | 6.3 | 28.1 |
| 5 | 1.29 | 6.1 | 34.3 |
| 6 | 1.28 | 6.1 | 40.4 |
| 7 | 1.21 | 5.8 | 46.1 |
| 8 | 1.14 | 5.4 | 51.5 |
| 9 | 1.09 | 5.2 | 56.7 |
| 10 | 1.00 | 4.8 | 61.5 |
| 11 | 0.95 | 4.5 | 66.0 |
| 12 | 0.92 | 4.4 | 70.4 |
| 13 | 0.88 | 4.2 | 74.6 |
| 14 | 0.83 | 4.0 | 78.5 |
| 15 | 0.79 | 3.8 | 82.3 |
| 16 | 0.78 | 3.7 | 86.0 |
| 17 | 0.73 | 3.5 | 89.5 |
| 18 | 0.63 | 3.0 | 92.5 |
| 19 | 0.59 | 2.8 | 95.3 |
| 20 | 0.51 | 2.4 | 97.7 |
| 21 | 0.48 | 2.3 | 100.0 |
| Total | 21.00 | 100.0 |
Here the first principal component explains only 7.8% of the variation. With 21 principal components, the average percentage of variability explained by a component is 1/21 = 0.48 or 4.8%. The average eigenvalue will be 1.00, since the 21 eigenvalues add up to 21. Hence in Table 1, the first component explains a lot more variability than we would expect if the variables were uncorrelated, 39.8% compared to 4.8%.
Principal component analysis is described as a method for reducing the dimensions of a set of data. With 21 separate measurements we have 21 dimensions to our outcome variables. But if we describe them instead by the first few principal components, we reduce the dimensions considerably. For example, in Table 1 the first five components explain 70.5% of the variability. We could just analyse these five components and discard the remaining 16. We would still have most of the information. The remaining components will consist mainly of measurement error anyway and will have little real information in them.
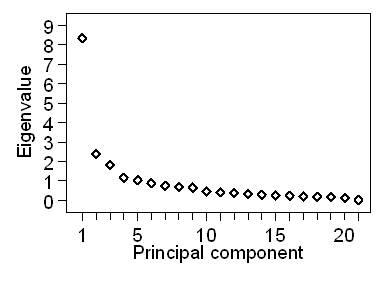
There are two frequently used methods used to decide how many dimensions our variables really have. One is the Kaiser criterion. This states that we take all those components with eigenvalues greater than the average, which is 1.00. So in Table 1, we would have five dimensions to our data. In Table 3, we would have 10. This cut-off should be about halfway down the table if the variables are not correlated. The other method is the Cattell scree plot. This is a plot of the eigenvalue against the principal component number. Figure 1 shows the scree plot for Table 1.
Figure 1. Scree plot for Table 1
It is called a scree plot because it resembled the scree formed by fallen rocks at the bottom of an escarpment. There are two fairly distinct parts to it, the large eigenvalues and the small eigenvalues, as shown in Figure 2.
Figure 2. Scree plot for Table 1 with lines fitted to the eigenvalues
We then form a judgement as to where the divide occurs. This is subjective and different observers may not agree what the dimension of the data is. For Figures 1 and 2, I think there are three dimensions and would not use more than the first three principal components. These would include 59.8% of the variability in the 21 variables. Although the scree plot is subjective, I think it produces a more useful answer than the objective Kaiser criterion.
Compare Figure 3, which shows the scree plot for the random numbers of Table 3.
Figure 3. Scree plot for Table 3
The eigenvalues all lie roughly along a single line, with no scree. We cannot reduce the dimensions of the problem.
In health research we often want to measure ill-defined and abstract things, like disability, depression, anxiety, and health. The obvious way to decide how depressed someone is to ask them. We could just ask ‘how depressed are you on a scale of 1 to 10?’, or use a visual analogue scale:
|-------------------------------------------------------------|
not at all
as depressed as it
depressed
is possible to be
but our subjects may not use that label for their problem. Instead we form a composite scale. We ask a series of questions relating to different aspects of depression and then combine them to give a depression score. For example, the depression scale of one such questionnaire, the General Health Questionnaire or GHQ (Goldberg and Hillier 1979) is shown in Figure 4.
| HAVE YOU RECENTLY | ||||
|---|---|---|---|---|
| 1. been thinking of yourself as a worthless person? | Not at all [ 0 ] | No more than usual [ 1 ] | Rather more than usual [ 2 ] | Much more than usual [ 3 ] |
| 2. felt that life is entirely hopeless? | Not at all [ 0 ] | No more than usual [ 1 ] | Rather more than usual [ 2 ] | Much more than usual [ 3 ] |
| 3. felt that life isn't worth living? | Not at all [ 0 ] | No more than usual [ 1 ] | Rather more than usual [ 2 ] | Much more than usual [ 3 ] |
| 4. thought of the possibility that you might make away with yourself? | Definitely have [ 3 ] | I don't think so [ 2 ] | Has crossed my mind [ 1 ] | Definitely not [ 0 ] |
| 5. found at times you couldn't do anything because your nerves were too bad? | Not at all [ 0 ] | No more than usual [ 1 ] | Rather more than usual [ 2 ] | Much more than usual [ 3 ] |
| 6. found yourself wishing you were dead and away from it all? | Not at all [ 0 ] | No more than usual [ 1 ] | Rather more than usual [ 2 ] | Much more than usual [ 3 ] |
| 7. found that the idea of taking your own life kept coming into your mind? | Definitely have [ 3 ] | I don't think so [ 2 ] | Has crossed my mind [ 1 ] | Definitely not [ 0 ] |
| (The numbers in [ ] are the scores for the answers. They do not appear on the questionnaire presented to the subject. The sum of these is the score on the depression scale.) | ||||
These are scored 0, 1, 2, 3 for the choices from left to right for items 1, 2, 3, 5, and 6, and 3, 2, 1, 0 for items 4 and 7. The sum of these is the score on the depression scale. The questions are clearly related to one another and together should make a scale. Anyone who truthfully gets a high score on this is depressed. The full questionnaire has four such scales.
To form questions into a scale, we first devise a set of questions which are expected to be related to the concepts of interest, based on experience. The questions are answered by test subjects. We then need to know whether the questions form a coherent scale and whether they measure one or more than one underlying construct. For example, Figure 5 shows a questionnaire, the Hull Reflux Cough Questionnaire, devised by Dr. Alyn Morice.
| Please circle the most appropriate response for each question | ||||||
|---|---|---|---|---|---|---|
| Within the last MONTH, how did the following problems affect you? | 0 = no problem and 5 = severe/frequent problem | |||||
| 1. Hoarseness or a problem with your voice | 0 | 1 | 2 | 3 | 4 | 5 |
| 2. Clearing your throat | 0 | 1 | 2 | 3 | 4 | 5 |
| 3. The feeling of something dripping down the back of your nose or throat | 0 | 1 | 2 | 3 | 4 | 5 |
| 4. Retching or vomiting when you cough | 0 | 1 | 2 | 3 | 4 | 5 |
| 5. Cough on first lying down or bending over | 0 | 1 | 2 | 3 | 4 | 5 |
| 6. Chest tightness or wheeze when coughing | 0 | 1 | 2 | 3 | 4 | 5 |
| 7. Heartburn, indigestion, stomach acid coming up (or do you take medications for this, if yes score 5) | 0 | 1 | 2 | 3 | 4 | 5 |
| 8. A tickle in your throat, or a lump in your throat | 0 | 1 | 2 | 3 | 4 | 5 |
| 9. Cough with eating (during or soon after meals) | 0 | 1 | 2 | 3 | 4 | 5 |
| 10. Cough with certain foods | 0 | 1 | 2 | 3 | 4 | 5 |
| 11. Cough when you get out of bed in the morning | 0 | 1 | 2 | 3 | 4 | 5 |
| 12. Cough brought on by singing or speaking (for example, on the telephone) | 0 | 1 | 2 | 3 | 4 | 5 |
| 13. Coughing more when awake rather than asleep | 0 | 1 | 2 | 3 | 4 | 5 |
| 14. A strange taste in your mouth | 0 | 1 | 2 | 3 | 4 | 5 |
| TOTAL SCORE _____________ /70 | ||||||
This questionnaire was devised using experience and evidence about the nature of respiratory symptoms. It gives a single score, but does it really measure one thing? To answer this we can do principal component analysis. The data were obtained from 83 attendees at a chronic cough clinic. The eigenvalues for the PCA are shown in Table 4.
| Component | Eigenvalue | Percentage of variability explained | Cumulative percentage of variability |
|---|---|---|---|
| 1 | 5.02 | 35.9 | 35.9 |
| 2 | 1.64 | 11.7 | 47.6 |
| 3 | 1.30 | 9.3 | 56.8 |
| 4 | 1.07 | 7.6 | 64.5 |
| 5 | 0.92 | 6.6 | 71.1 |
| 6 | 0.74 | 5.3 | 76.4 |
| 7 | 0.68 | 4.9 | 81.2 |
| 8 | 0.59 | 4.2 | 85.4 |
| 9 | 0.44 | 3.1 | 88.6 |
| 10 | 0.39 | 2.8 | 91.4 |
| 11 | 0.36 | 2.6 | 93.9 |
| 12 | 0.34 | 2.4 | 96.3 |
| 13 | 0.26 | 1.9 | 98.2 |
| 14 | 0.25 | 1.8 | 100.0 |
| Total | 14.00 | 100.0 |
The scree plot is shown in Figure 6.
Figure 6. Scree plot for Table 4
By the Kaiser criterion for Table 4, we would have four dimensions. From the scree plot in Figure 6, two or three dimensions looks better. We shall try both two and three dimensions.
Having decided the dimensions of the data, we now need to find a good description of them. To do this we use factor analysis, described below.
There are many types of scale in regular use. This is one of several possible formats. Scales are difficult to design and validate, and so whenever possible we use one which has been developed previously, such as the GHQ. This also makes it easier to plan and to interpret the results of studies, as the properties of the scale are already known. There is a wide range of scales which have been used in many studies, and are readily available to the researcher. A review of the literature in the field in which you propose to research will reveal what scales are available and which are used most often. It should then be possible to find information about the performance of the scales, such as measurement error, to help in choosing one for you.
McDowell and Newell (1996) review a large number of scales useful in medical research, including full lists of questions. Bowling (1997) gives a review of quality of life scales.
Factor analysis is a statistical method developed by psychologists. It was originally introduced by to answer questions like ‘Is there more than one kind of intelligence?’. By carrying out principal component analysis on a set of variables, we can decide whether there is more than one dimension. There are other methods to do this as well, but we shall stick to PCA for this lecture. Stata, for example, offers methods called principal factor (the default), iterated principal factor, and maximum likelihood, in addition to principal component analysis. SPSS offers seven methods and has principal component analysis as the default.
The factor analysis model is that each of our variables can be represented as a linear combination of other variables, called factors, which we cannot actually see. The factors are all set to have mean zero and variance one. Each observed variable is the sum of each factor multiplied by a coefficient plus some unique factor of its own. The coefficients are called factor loadings.
Table 5 shows the factor loadings for two factors, which are the first two principal components.
| Variable | Factor Loadings | ||
|---|---|---|---|
| Factor 1 | Factor 2 | Uniqueness | |
| hoarse | 0.64 | –0.11 | 0.57 |
| throat | 0.58 | –0.58 | 0.33 |
| mucus | 0.60 | –0.33 | 0.53 |
| retching | 0.62 | 0.21 | 0.57 |
| lyingdwn | 0.66 | 0.24 | 0.51 |
| wheeze | 0.67 | 0.12 | 0.53 |
| heartbrn | 0.41 | 0.45 | 0.64 |
| tickle | 0.64 | –0.18 | 0.56 |
| eating | 0.75 | 0.15 | 0.42 |
| foods | 0.65 | 0.48 | 0.35 |
| outofbed | 0.58 | –0.22 | 0.61 |
| speaking | 0.62 | –0.38 | 0.47 |
| day | 0.39 | –0.33 | 0.74 |
| taste | 0.46 | 0.53 | 0.51 |
The uniqueness is the coefficient by which we would multiply a standard Normal variable by to give the extra error not explained by the factors. Hence we predict that the standardised value of the first variable, hoarse, is given by
hoarse = 0.64 × factor 1 – 0.11 × factor 2 + 0.57 × error
where error is a Standard Normal random variable.
Such factors are called latent variables. A dictionary definition of ‘latent’ is that it is concealed, not visible or apparent, dormant, undeveloped, but capable of development. In statistics, we mean something which is not measured directly and the existence of which is inferred in some way. We can estimate the numerical values of the factors from sets of coefficients like those of Table 2. These are not the same as the factor loadings. The factor loadings are for calculating the variables from the factors, the factor coefficients are for calculating the factors from the variables.
In Table 5, most of the loadings for Factor 1 are positive numbers and mostly of similar size. The loadings for Factor 2 tend to be smaller and half of them are negative. If we can predict our variables from two factors, we could also predict them from two other factors, each of which is a linear combination of the first two. This is called a factor rotation.
For example,
hoarse = 0.64 × factor1 – 0.11 × factor2 + 0.57 × error
Define two new variables, new1 and new2, so that
new1 = factor1 + factor2
new2 = factor1 – factor2.
Then
factor1 = (new1 + new2)/2
factor2 = (new1 – new2)/2
If we replace the old factors by the new:
hoarse = 0.64 × (new1 + new2)/2 – 0.11 × (new1 – new2)/2 + 0.57 × error
= 0.27 × new1 + 0.38 × new2 + 0.57 × error
There are many possible new pairs of factors which we could use. We will only use rotations which keep the standard deviations of the factors equal to one, which this example does not. Note that the uniqueness remains the same.
We find a rotation to produce two new factors which have as many factor loadings as close to zero as possible. This means that as many variables as possible will be predicted mainly by only one factor. This in turn helps us to interpret the factors. Table 6 shows the factor loadings after a rotation.
| Variable | Factor Loadings | ||
|---|---|---|---|
| Factor 1 | Factor 2 | Uniqueness | |
| hoarse | 0.53 | 0.38 | 0.57 |
| throat | 0.82 | 0.01 | 0.33 |
| mucus | 0.65 | 0.19 | 0.53 |
| retching | 0.28 | 0.59 | 0.57 |
| lyingdwn | 0.29 | 0.64 | 0.51 |
| wheeze | 0.39 | 0.57 | 0.53 |
| heartbrn | –0.03 | 0.60 | 0.64 |
| tickle | 0.58 | 0.33 | 0.56 |
| eating | 0.42 | 0.64 | 0.42 |
| foods | 0.11 | 0.80 | 0.35 |
| outofbed | 0.57 | 0.26 | 0.61 |
| speaking | 0.71 | 0.17 | 0.47 |
| day | 0.51 | 0.05 | 0.74 |
| taste | –0.06 | 0.70 | 0.51 |
There are several methods of rotation; Table 6 is the result of a varimax rotation, which keeps the factors uncorrelated. It is also possible to have correlated factors. Rotations methods which produce them are called oblique. Methods for rotation have names like quartimax, promax, quartimin, oblimax, and oblimin.
In Table 6, Factor 1 mainly loads on hoarseness, clearing the throat, feeling of mucus, tickle in the throat, cough on getting out of bed, cough on singing or speaking, and cough more when awake. Factor 2 mainly loads on retching when cough, cough on lying down, tightness or wheeze, heartburn, cough with eating, cough with foods, and taste in the mouth. We then have the task of deciding from this what each factor represents. We might, for example, label them as ‘respiratory tract cough’ and ‘alimentary tract cough’.
Table7 shows the factor loadings after a rotation of three factors.
| Variable | Factor Loadings | |||
|---|---|---|---|---|
| Factor 1 | Factor 2 | Factor 3 | Uniqueness | |
| hoarse | 0.61 | 0.35 | 0.07 | 0.49 |
| throat | 0.76 | –0.08 | 0.32 | 0.31 |
| mucus | 0.73 | 0.16 | 0.07 | 0.43 |
| retching | 0.06 | 0.47 | 0.63 | 0.37 |
| lyingdwn | 0.19 | 0.56 | 0.41 | 0.34 |
| wheeze | 0.47 | 0.55 | 0.08 | 0.35 |
| heartbrn | 0.21 | 0.67 | –0.31 | 0.31 |
| tickle | 0.67 | 0.30 | 0.06 | 0.40 |
| eating | 0.33 | 0.55 | 0.43 | 0.38 |
| foods | 0.13 | 0.77 | 0.20 | 0.29 |
| outofbed | 0.23 | 0.10 | 0.83 | 0.26 |
| speaking | 0.68 | 0.10 | 0.27 | 0.33 |
| day | 0.29 | –0.07 | 0.54 | 0.29 |
| taste | –0.09 | 0.67 | 0.22 | 0.43 |
In Table7, Factor 1 mainly loads on hoarseness, clearing the throat, feeling of mucus, tickle in the throat, and cough on singing or speaking. Factor 2 mainly loads on cough on lying down, tightness or wheeze, heartburn, cough with eating, cough with foods, and taste in the mouth. Factor 3 mainly loads on retching when cough, cough on getting out of bed, and cough more when awake. We can consider whether this gives us a more interpretable set of factors than the two factor rotation. Factor 1 is now clearly ‘throat cough’ and Factor 2 is ‘alimentary tract cough’, though wheeze is anomalous. Factor 3 is not so clear. We might consider discarding those items and trying again.
Table 8 shows the coefficients for calculating the three factors.
| Variable | Factor Coefficents | ||
|---|---|---|---|
| Factor 1 | Factor 2 | Factor 3 | |
| hoarse | 0.23 | 0.06 | –0.12 |
| throat | 0.31 | –0.19 | 0.07 |
| mucus | 0.31 | –0.04 | –0.11 |
| retching | –0.16 | 0.12 | 0.33 |
| lyingdwn | –0.07 | 0.17 | 0.15 |
| wheeze | 0.13 | 0.17 | –0.11 |
| heartbrn | 0.06 | 0.32 | –0.33 |
| tickle | 0.26 | 0.03 | –0.13 |
| eating | –0.01 | 0.15 | 0.14 |
| foods | –0.09 | 0.31 | 0.00 |
| outofbed | –0.06 | –0.10 | 0.48 |
| speaking | 0.26 | –0.09 | 0.03 |
| day | 0.05 | –0.15 | 0.30 |
| taste | –0.18 | 0.29 | 0.06 |
Mostly the variables which have high factor loads have high coefficients too, though there are one or two anomalies. Heartburn, for example, has quite a high (negative) coefficient for factor 3, but does not load highly on it. We could include heartburn in the scale, subtracting its score from the sum of the other three items.
Having decided that a group of variables make up our scale, we might then simplify by making the coefficients for them all one and adding. Thus the ‘throat cough scale’ becomes the sum of the scores for hoarseness, clearing the throat, feeling of mucus, tickle in the throat, and cough on singing or speaking.
If a series of items are to form a scale, they should be correlated with one another. A useful coefficient for assessing internal consistency is Cronbach's alpha (Cronbach 1951). Alpha is a measure of how closely the items that make up the scale are correlated. If the items are all perfectly correlated, which usually means identical, then alpha will be one, its maximum possible value. If the items are all independent, having no relationship at all, then alpha will be zero. In this case, of course, there is no coherent scale formed by summing them.
Mathematically, the coefficient alpha is given by:

where k is the number of items, σi2 is the variance of the i'th item and σT2 is the variance of the total scale formed by summing all the items. So the essential part of alpha is the sum of the variances of the items divided by the variance of the sum of all the items. If the items are all independent, then the variance of the sum will be the sum of the individual variances, σT2 = Σσi2. The ratio will be one and α = 0. If the items are all identical and so perfectly correlated, all the σi2 will be equal and σT2 = k2σi2. Because all the item variances are the same, Σσi2 = kσi2, so = Σσi2/σT2 = 1/k and α = 1.
For the three scales found in the Hull Reflux Cough Questionnaire example, the alpha coefficients are
| Scale | alpha |
|---|---|
| 1 | 0.78 |
| 2 | 0.79 |
| 3 | 0.68 (without heartburn) |
| 3 | 0.53 (with heartburn as negative item) |
This would suggest that we would be better off omitting heartburn from Scale 3, but in any case Scale 3 has poorer consistency than Scales 1 and 2. For the whole Hull Reflux Cough Questionnaire scale, with 14 items, alpha = 0.86, better than the three subscales, so it is a fairly consistent scale.
Alpha is based on the idea that our items are a sample from a large population of possible items which could be used to measure the construct which the scale represents. If alpha is low, then the items will not be coherent and the scale will not necessarily be a good estimate of the construct. Alpha can be thought of as an estimate of the correlation between the scale and another similar scale made from a different set of the possible items.
For use in research, alpha values of 0.7 or 0.8 are considered acceptable. A very high value, like 0.95, might indicate some redundancy in the scale, because if our items are very highly correlated we may not need them all. For use in making clinical decisions about individual patients, it is considered that alpha should be higher, say 0.9 or greater.
Alpha is often called a coefficient of reliability, or alpha reliability. It is not the same as the correlation between repeated administrations of the scale, but if the model is correct it should be similar.
We can increase alpha by adding in more items, though the gain gets smaller as the number of items in the scale increases. We can increase alpha by dropping items which are not highly correlated with others in the scale. For example, heartburn has weaker correlations with retching, out of bed, and during the day than any of these have with one another.
Factor analysis is often treated very sceptically by statisticians. For example, Feinstein (2001, page 263) quoted Donald Mainland: ‘If you don’t know what you’re doing, factor analysis is a great way to do it.’ There is actually a book called Factor Analysis as a Statistical Method (Lawley and Maxwell 1971), which would imply that readers might not think of factor analysis as a statistical method at all!
There are several problems with factor analysis.
For all these reasons, we need to test our scales, by repeating them among other groups of subjects, by estimating their repeatability, and by comparing them with other observations. We shall describe strategies for doing this in Week 8.
Despite all these caveats, factor analysis remains the main method for establishing composite scales. Apart from simply going on expert opinion, there is not much else to do. It is also a complicated process, full of choices and pitfalls, and not to be undertaken lightly! Don’t try this at home. If you are going to do factor analysis ‘for real’ you should consult an expert.
For more on factor analysis, see Streiner and Norman (2003).
Bowling, A. (1997) Measuring Health: A Review Of Quality Of Life Measurement Scales 2nd Ed. Open University Press.
Cronbach, LJ. (1951) Coefficient alpha and the internal structure of tests. Psychometrika 16, 297-334.
Feinstein A. (2001) Principles of Medical Statistics. CRC Press.
Goldberg DP and Hillier VF. (1979) Scaled version of the general health questionnaire. Psychological Medicine 9, 139-145.
Lawley DN and Maxwell AE. (1971) Factor Analysis as a Statistical Method, 2nd. Ed. Butterworth.
McDowell, I. and Newell, C. (1996) Measuring Health: A Guide To Rating Scales And Questionnaires, 2nd Ed. Oxford University Press
Motallebzadeh R, Bland JM, Markus HS, Kaski JC, Jahangiri M. (2007) Neurocognitive function and cerebral emboli: randomised study of on-pump versus off-pump coronary artery bypass surgery. Annals of Thoracic Surgery 83, 475-82.
Streiner, D.L. and Norman, G.R. (2003) Health Measurement Scales: A Practical Guide To Their Development And Use, 3rd Ed. Oxford University Press
To Measurement in Health and Disease index.
To Martin Bland's M.Sc. index.
This page maintained by Martin Bland.
Last updated: 23 May, 2008.