Brush up your maths: Simple maths test 2007

The test

There were ten questions:

  1. 627 + 183 = ?

  2. 20 – 3 × 5 = ?

  3. Put these numbers in order of magnitude from biggest to smallest:
    0.5   0.03   1   0.1   1.5   0.3   0.55   0.05

  4. 0.001 is equal to which of the following?
            1               1                   1
    (a) –––     (b) ––––     (c) –––––
          10             100             1000

  5. ¾ + 0.6 = ?

  6. If y = x – 2, what is the value of x when y = 6?

  7. Write 3.75 million in figures.

  8. √(32 + 42) = ?

  9. What is 2½% of £10?

  10. If cheese is £2.20 per kilogramme, what should I pay for 400 grammes?

The answers are:

  1. 627 + 183 = 810

  2. 20 – 3 × 5 = 5.
    Note that the order of operations in maths is brackets, powers of, divide, multiply, add, subtract.

  3. Put these numbers in order of magnitude from biggest to smallest:
    0.5   0.03   1   0.1   1.5   0.3   0.55   0.05
    gives us
    1.5   1   0.55   0.5   0.3   0.1   0.05   0.03.
    I carelessly gave:
    0.03   0.05   0.1   0.3   0.5   0.55   1   1.5,
    arranged in ascending order. I counted either as correct.

  4. 0.001 is equal to which of the following?
            1               1                   1
    (a) –––     (b) ––––     (c) –––––
          10             100             1000
    The answer is c.

  5. ¾ + 0.6 = 0.75 + 0.6 = 1.35.
    I would also accept 1 7/20 or 27/20.

  6. If y = x – 2, the value of x when y = 6 is 8.

  7. Write 3.75 million in figures: 3,750,000.

  8. √(32 + 42) = √(9 + 16) = √25 = 5.

  9. 2½% of £10 = £0.25 = 25p.

  10. If cheese is £2.20 per kilogramme, for 400 grammes I should pay £2.20 × 400/1000 = £0.88 = 88p.

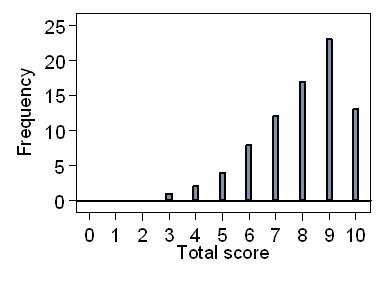
There were 80 students altogether. The numbers getting each possible score out of 10 were:

Score Count %
0 0 0.00
1 0 0.00
2 0 0.00
3 1 1.25
4 2 2.50
5 4 5.00
6 8 10.00
7 12 15.00
8 17 21.25
9 23 28.75
10 13 16.25

We can present this graphically:

Hence 27 students got 7 or less, the score that I suggested meant that they should brush up their maths.

The question which caused most trouble was 2: 20 – 3 × 5 = ?. 62% got this wrong, almost all giving the answer 85. They got this by first subtracting 3 from 20 then multiplying 17 by 5. The rules of arithmetic are that we multiply before we add. We do not need brackets to make this clear. See part 1 of Brush up your maths.

We asked whether you panicked when you saw all those numbers. 37 said 'yes' to this, 35 said 'no', and 8 did not reply. Not surprisingly, the panickers did worst, with mean score = 7.3, compared to 8.6 for those who did not panic and 8.3 for those who did not answer.

I was disappointed that only 41 identified themselves, making it difficult for us to see how this test might predict student performance. Anonymous students were more likely to panic, 59.0% compared to 34.2% of identified students. Anonymous students had a lower average score, 7.3 compared to 8.5 for identified students.

Martin Bland
15 October, 2007.

Back to Brush up your maths main menu.

To Martin Bland's M.Sc. index.

To Martin Bland's home page.

This page maintained by Martin Bland.
Last updated: 18 October, 2007.

Back to top.