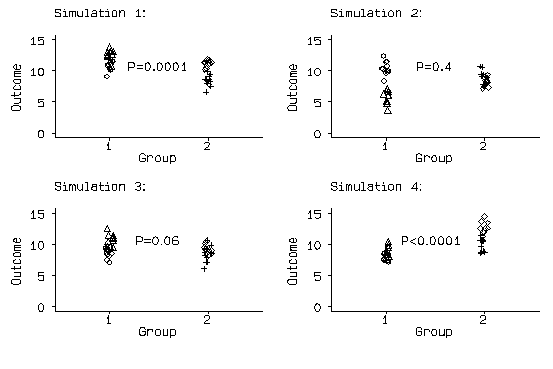 d
d
Published (in part) as: Bland JM. (2004) Cluster randomised trials in the medical literature: two bibliometric surveys. BMC Medical Research Methodology 4, 21.
Talk first presented to the RSS Medical Section and RSS Liverpool Local Group, 12 November 2003.
If a cluster-randomised trial is analysed without recognition of the clustering, the analysis will ignore the possible correlation between members of the same cluster. When positively correlated observations are treated as independent, the result may be standard errors which are too small, confidence intervals which are too narrow, and P values which are too small, leading to conclusions which may be false. I shall describe the analysis of some published trials and give a biased and partial review of the history and current situation.
I shall state at the outset that I have in past ignored clustering in the analysis of clustered designs. I suspect that many medical statisticians have done the same.
If P values are too small, we will detect differences where none exist more frequently than the 5% of tests which we expect to be significant when the null hypothesis is true. To illustrate this effect I carried out a little simulation. I generated four cluster means, two in each group, from a Normal distribution with mean 10 and standard deviation 2. I then generated the 10 members of each cluster by adding a random number from a Normal distribution with mean zero and standard deviation 1. Thus the null hypothesis, that there is no difference between the means in the two groups, is true. I then carried out a two-sample t test comparing the means, ignoring the clustering.
The results of the first four simulations are shown in the following figure:
Figure 1. Simulation of a small cluster-randomised trial, first four runs.
The first difference is highly significant, with the mean in group 1 exceeding the mean in group 2, and the fourth is highly significant, but the means are the other way round.
I ran this simulation 1000 times and obtained 600 significant differences with P<0.05, of which 502 were highly significant, with P<0.01. If the t test ignoring the clustering were a valid test, we would expect 50 significant differences, i.e. 5% of 1000, and 10 highly significant ones. The reason for this is that the analysis assumes that we have 20 independent observations in each group. This is not true. We have two independent clusters of observations, but the observations in those clusters are really the same thing repeated ten times. This is fairly obvious in the figure:
This makes the standard deviation smaller than it should be, and the number of observations larger than it should be, which makes the standard error smaller than it should be, which in turn makes the t statistic bigger than it should be. It also makes the degrees of freedom bigger than it should be. These combine to make the P value smaller than it should be.
My simulation is very extreme, with two groups of two clusters and a very large cluster effect. However, I have been a referee for a grant proposal for a cluster randomised trial with two groups of two clusters, and a smaller cluster effect would only reduce the shrinking of the P values, it would not remove it. The simulation shows that spurious significant differences can occur if we ignore the clustering.
When P values tend to be too big, and we miss significant difference, we don't like it, but we can put up with it. A non-significant difference means that we have failed to show that something, such as a difference or relationship, exists, but we do not conclude that the thing does not exist. At least, we should not conclude this if we understand statistics. Hence we cannot be misled by such methods, though we can miss things. They are called conservative. P values which are too small lead us to conclude that there is strong evidence that the thing exists, when in fact there is no such thing. Thus we may end up knowing something which ain't so. If a statistician has to be wrong, he/she wants to be wrong in the conservative direction, rather like certain Labour party politicians.
The magnitude of the effect of clustering is measured by the design effect, Deff, given by the following:
Deff = 1 + (m - 1)xICC
where m is the number of observations in a cluster and ICC is the intra-cluster correlation coefficient.
The ICC is the correlation between pairs of subjects chosen at random from the same cluster. It is usually quite small, 0.04 is a typical figure. This was the median ICC reported in the review by Eldridge et al. (2003). If m=1, cluster size one, in other words, no clustering, then Deff=1, otherwise Deff will exceed 1.
We can use this in two ways. In design, if we estimate the required sample size ignoring clustering, we must multiply it by the design effect to get the sample size required for the clustered sample. Alternatively, we can say that if the sample size is estimated ignoring the clustering, the clustered sample has the same power as for a simple sample of size equal to what we get if we divide our sample size by the design effect.
In analysis, if we analyse the data as if there were no clusters, the variances of the estimates must be multiplied by Deff, hence the standard error must be multiplied by the square root of Deff.
From this formula, we can see that clustering may have a large effect if the ICC is large OR if the cluster size is large. Only one of these conditions need be met. For example, if the ICC is 0.001, a very small correlation, and the cluster size is 500, the design effect will be 1 + (500-1)x0.001 = 1.5 and we would need to increase the sample size by 50% to achieve the same power as an unclustered trial.
In addition, we need to estimate variances both within and between clusters. If the number of clusters is small, the between clusters variance will have few degrees of freedom and we will be using the t distribution in inference rather than the Normal. This too will cost in terms of power.
A study where the cluster size is small, there are a large number of clusters, and the ICC is small will have a design effect close to one and it will have little effect if the clustering is ignored. For example, in a randomised controlled trial of the effects of coordinating care for terminally ill cancer patients (Addington-Hall et al., 1992), 554 patients were randomised by GP. There were about 200 GPs whose patients might be eligible for the study, and so most clusters had only a few patients. I decided for simplicity that the person analysing the trial could ignore the clustering and so did not raise the issue.
There are several possible approaches to get a valid statistical analysis. One possible analysis which should be correct is to find the means for the four clusters and carry out a two-sample t test using these four means only. When I did this for my 1000 simulation runs, I got 53, 5.3% to be significant, and 14, 1.4% to be highly significant, very close to what we would expect from a valid test.
There are several approaches which can be used to allow for clustering. The easiest is to calculate a summary statistic for each cluster. This is usually a mean for a continuous outcome or a proportion for a dichotomous outcome. This approach has the great advantage of being simple, but it cannot allow for individual covariates.
We can also:
I do not wish to go into any of these in this talk. As far as I am concerned, any method which takes into account the clustering will be a vast improvement compared to methods which do not.
As an example of a cluster randomised trial I shall take the The Swedish Two-County Trial of mammographic screening.
A problem particular to screening trials is contamination of the control group by the screening process. This may be because widespread publicity is needed to encourage women to come for screening, or because members of the screening group pass on information to neighbours who have been allocated to control, leading them to demand screening. This can be countered by using a larger sampling unit than the individual. We might, for example allocated whole towns to screening or control. In the Swedish Two Counties Study of breast cancer screening (Tabar and Gad, 1981, Tabar et al., 1985), the county of Kopparberg was divided into 7 geographical areas. Each of these was subdivided into three units, which were either parishes or municipalities, two of which were randomly allocated to screening and the other to control. The county of ™sterg”tland was divided into 12 areas, each of which was subdivided into two units, one unit being allocated to screening and the other to control.
There is a price to be paid for this at the analysis stage. We can no longer think of our trial subjects as independent individuals, but must do the analysis at the level of the sampling unit, the parish for the Two Counties Study. This is because we have two sources of variation, that between people in an area and that between areas, and the variability between areas must be taken into account. This leads to a loss of power and a need to increase the sample size. The larger and fewer our sampling units, the more important this becomes. This feature of the design is often not appreciated by researchers. Tabar et al. (1985) state that 'the statistical analysis with Mantel Haenszel techniques was based on individuals. The excess variation resulting from randomisation being at the community rather than the individual level was negligible.' No data are presented to support this statement. Is their analysis correct? It is surely open to question.
This study was later analysed by Duffy et al. (2003) who used hierarchical modelling to take clustering into account, and found evidence for an effect. Taking account of the cluster randomisation there was a significant 30% reduction in breast cancer mortality in the ASP. They concluded that mammographic screening does indeed reduce mortality from breast cancer, and that the criticisms of the Swedish Two-County Trial are unfounded.
I think that the criticism was well founded. It was wrong to ignore the clustering in such a study. The fact that we get the same answer when we do it correctly is irrelevant.
An interesting case was a paper sent to me in 1997 by the British Medical Journal. This gave me great pleasure, as it managed to include several of my favourite statistical errors.
It was a study of the impact of a specialist outreach team on the quality of nursing and residential home care. The intervention was carried out at the residential home level. Eligible homes were put into matched pairs and one of each pair randomised to intervention. Thus the randomisation was clustered. This intervention was applied to the care staff, not to the patients. The residents in the home were used to monitor the effect of the intervention on the staff.
The clustering was totally ignored in the analysis. What they did was to use the patient as the unit of analysis, then carry out a Mann-Whitney test of the difference between the scores of the two groups at baseline. This is an unnecessary and pointless test. The test was not significant, as we might expect, the homes being randomised, although ignoring clustering may increase the chance of a Type I error, a false positive difference. They then did the same test for the data collected at follow-up, completely ignoring the baseline measurements. Of course, the fact that the difference is not significant at baseline does not mean we should ignore it. It is unlikely that follow-up score is unrelated to the base-line at the patient level and much residual variability could be removed by allowing for it. As neither of these Mann-Whitney tests was significant, the authors then did a Wilcoxon matched pairs test for each group separately and found that one was significant and the other not. 'Not significant' means only that we have failed to detect a difference, not that there isn't one, so the comparison of these two paired tests was meaningless.
I suggested two possible approaches to the analysis. We could use a summary statistic for the home, e.g. the mean change in score or mean cost. These could then be compared using a t method. As the homes were randomised within pairs, I suggested that the paired t method would be appropriate. (This may not be right, as the matching variables may not be informative and the loss of degrees of freedom may be a problem. We live and learn, I hope.) The results should be given as a difference in mean change, with a confidence interval as recommended in the BMJ's guide-lines, rather than as a P value. (I seem to say this often.) The alternative approach would be to fit a multi-level model, with homes as one level of variability, subjects another, and variation within subjects a third. This, I thought, was strictly a job for a professional statistician. I thought that a simple summary measure analysis would suffice.
The paper was rejected. Time passed and I became curious about the ultimate fate of this paper. I search on the
author's name and found the study reported in the Lancet! There was an extra author, a well-known medical
statistician. Here is an extract:
'The unit of randomisation in the study was the residential home and not the resident. Thus, all data were analysed
by use of general estimated equation models to adjust for clustering effects within homes. . . . Clinical data are
presented as means with 95% CIs calculated with Huber variance estimates.'
Huber variance estimates are adjusted for clustering, and now you know as much as I do about them. Clearly, all my referee's comments and suggestions had been acted upon. It had been a good day's work. I looked for the acknowledgement to an unknown referee, but in vain.
About this time began a rash of how-to-do-it papers, statistics notes in the BMJ, articles in GP journals, special editions of Statistical Methods in Medical Research and Statistics in Medicine, and papers reporting intraclass correlation coefficients to help others to design clustered studies.
Figure 2. Results of a Web of Science search on: randomi* in clusters OR cluster randomi*
Figure 2 shows the result of a search on the Web of Science, looking for papers on cluster randomisation. I used the terms 'randomi* in clusters OR cluster randomi*' in title or abstract. This was designed to detect both the 'z' ands 's' spellings of 'randomized' and 'randomization'. I found that other terms, such as 'group randomised' did not work, as I got hundreds of abstracts with 'patients were in two groups, randomised to active or control treatments'. Hence this is not a thorough search and will have missed many studies, but it gives an idea of the increase in activity. I divided the papers into those which were methodological, either educating researchers into the appropriate design and analysis of cluster randomised trials or developing new methods of analysing such trials, and those reporting actual trials. The data for 2001 includes special issues of Statistics in Medicine and Statistical Methods in Medical Research on cluster randomisation, so there were a larger number of methodological papers than might be expected in that year. I found it interesting that the numbers of papers found in the two categories were similar in each year before 2001, so I found as many papers about how to do such trials as I found trials themselves. I find it hard to believe that there are so few such trials being reported and think it likely that many are being reported without any acknowledgement of the importance of clustering.
All the papers up to 1990 are due to Alan Donner and his colleagues. However, as noted above, I found it impossible to identify papers which used older terminology. A paper by Cornfield (1978) 'Randomisation by group: A formal analysis' includes the following statement 'Randomization by cluster accompanied by an analysis appropriate to randomization by individual is an exercise in self-deception, however, and should be discouraged.' This would not be found by my search. The book on cluster randomization by Murray (1998) is called The Design and Analysis of Group-Randomized Trials. As a search of journals, this also misses the important book by Donner A, Klar N. (2000) Design and Analysis of Cluster Randomised Trials in Health Research. The search also ignores papers using clusters in observational studies. These would be harder to identify. I suspect there are few of them, either methodological or reports of studies which allow for clustering, though there are many cluster sampled observational studies which do not allow for it.
An interesting development in reporting has been introduced by the British Medical Journal, which around 1999 began to include a description of the trial design in the title of the paper, for example 'Effect on hip fractures of increased use of hip protectors in nursing homes: cluster randomised controlled trial' (Meyer et al. 2003) and 'Insecticide impregnated curtains to control domestic transmission of cutaneous leishmaniasis in Venezuela: cluster randomised trial' (Kroeger et al. 2002). As an aside, I must point out that these design descriptions are not always correct. For example, a paper by Hildebrand et al. (2000) was titled 'Risk among gastroenterologists of acquiring Helicobacter pylori infection: case-control study'. These authors identified a group of gastroenterologists and a group from the general population and followed them for three years, testing for H pylori infection. Here being a gastroenterologist is the exposure, not the disease. A case-control study would start with people who are infected with H pylori and people who were not, then find out whether they were gastroenterologists. I am reliably informed that in the title of at least one paper the incorrect design description was added by the BMJ. Having to include a description of the study design in the title must concentrate the mind of researchers considerably. Nor does the cluster randomised nature of the trial necessarily appear in the description. For example, 'Effects of alternative maternal micronutrient supplements on low birth weight in rural Nepal: double blind randomised community trial' (Christian et al. 2003) was a cluster randomised trial.
In 1998, Alan Donner, author of that 1982 paper and of many others on the topic, came to a meeting on cluster-randomised trials in Oxford. This was organized by Doug Altman's group, who invited statisticians from around the UK who had an interest in this subject, including Sally Kerry and myself. Alan Donner was delighted to be in same room with so many people who cared about cluster randomization. He had thought nobody apart from himself was interested in the subject, having got very little reaction to his work in North America. But in the UK it was clearly an idea for which the time had come.
I wondered why this should be, and suggest the following. In the UK we have the National Health Service (NHS), which, whether or not it is wonderful for patients, is certainly wonderful for researchers. Everyone in the UK is registered with one and only one NHS General Practice (primary care centre). Access to all other NHS care except emergency is via these general practices. It is therefore possible to randomise practices to different types of care policies, health promotion policies, or referral policies. The Medical Research Council (MRC) has a research framework of practices where a research nurse is funded by MRC to facilitate research. There are now other, similar networks of general practices, where research-minded GPs have got together. Hence, the UK is peculiarly well suited to cluster-based research in healthcare. I suspect that this has stimulated the interest in clusters among UK medical statisticians.
There have been several reviews of published cluster randomised trials. Problems of identifying trials, e.g. Donner et al. (1990), Simpson et al. (1995), Puffer et al., (2003), and Isaakidis and Ioannidis (2003). All but Puffer et al. (2003) reported that very few trials had sample size calculations which included clustering and about half took clustering into account in analysis, fewer in the African studies reported by Isaakidis and Ioannidis (2003). Puffer et al. (2003) reported recent (1997-2002) trials in British Medical Journal, Lancet, and New England Journal of Medicine. They did not mention any trials which failed to take clustering into account. However, they did have some where clustering was ignored in the analysis. My own review of their trials as listed on the BMJ website found 3 out of 36.
| Authors | Source | Years | Clustering allowed for in sample size | Clustering allowed for in analysis |
|---|---|---|---|---|
| Donner et al. (1990) | 16 non-therapeutic intervention trials | 1979 - 1989 | <20% | <50% |
| Simpson et al. (1995) | 21 trials from American Journal of Public Health and Preventive Medicine | 1990 - 1993 | 19% | 57% |
| Isaakidis and Ioannidis (2003) | 51 trials in Sub-Saharan Africa | 1973 - 2001 (half post 1995) | 20% | 37% |
| Puffer et al. (2003) | 36 trials in British Medical Journal, Lancet, and New England Journal of Medicine | 1997 - 2002 | 56% | 92% |
| Eldridge et al. (2003) | 152 trials in primary health care | 1997 - 2000 | 20% | 59% |
To identify cluster randomised trials we have to read the trials. We cannot tell from title, keywords, or abstract. The problem papers are those where the authors are not aware of clustering and do not mention it.
My strategy was to choose some journals likely to contain cluster randomised trials, such as the British Medical Journal, Lancet, Journal of the Royal College of General Practitioners, etc., and scan some likely years (1983, 1993, 2003) for cluster randomised trials. I decided to start with the British Medical Journal and scan one volume (six months) for each of these years. The yield was much lower than I anticipated. I therefore increased the search to the full year and added 1988 and 1998. References for all the papers found are given in the Appendix. The results are shown in Table 2.
| Year | Vol | Trials | Clustering ignored | Important? |
|---|---|---|---|---|
| 2003 | 326-7 | 9 | 0 | 0 |
| 1998 | 316-7 | 4 | 1(?) | 1 |
| 1993 | 306-7 | 4 | 3 | 2 |
| 1988 | 296-7 | 0 | 0 | 0 |
| 1983 | 286-7 | 1 | 1 | 1 |
Papers for 2003 go up 8th November.
The query is because the authors stated that 'Univariate comparisons were calculated by t test and chi-squared analysis. The role of potential covariates was explored using linear regression specified as a two level model (practice and individual) using the software package MLn.' (Wright et al., 1998). I could find no multilevel modelling in the paper, but a lot of t and chi-squared tests. This was a trial of community based management in failure to thrive by babies. 38 primary care teams were randomly allocated to intervention or control and all children identified in the practice were offered the same intervention, so clearly cluster should be taken into account.
Russell et al. (1983) investigated the effect of nicotine chewing gum as an adjunct to general-practitioners advice against smoking. Subjects were 'assigned by week of attendance (in a balanced design) to one of three groups (a) non-intervention controls (b) advice and booklet (c) advice and booklet plus the offer of nicotine gum. There were 6 practices, with recruitment over 3 weeks, one week to each regime. The study was analysed by chi-squared tests. As there were 1938 subjects in 18 clusters, clustering should have been taken into account.
Rink et al. (1993) investigated the impact of introducing near patient testing for standard investigations in general practice. 12 practices were used, and some given the equipment and some not in a cross-over design. Analysis used paired t tests, unpaired t tests, odds ratios, ratios of proportions with confidence intervals, and chi-squared tests. Yes, they were at St. George's and just along the corridor from myself and in the same department as Sally Kerry.
In a trial of clinical guidelines to improve general-practice management and referral of infertile couples, Emslie et al. (1993) randomised 82 general practices in Grampian region and studied 100 couples in each group. However, the main outcome measure was whether the general practitioner had taken a full sexual history and examined and investigated both partners appropriately, so the GP should quite definitely be the unit of analysis here.
The trial where I judged ignoring clustering to be unimportant had many very small clusters. Wetsteyn and Degeus (1993) compared 3 regimens for malaria prophylaxis in travellers to Africa. Members of one family were allocated to one regimen and the results analysed using a chi-squared test.
Many methods were used to analyse trials where the authors were aware of the importance of clustering (Table 3). Some authors used more than one method.
| Method | Papers |
|---|---|
| Summary statistics for cluster | Coulthard et al. (2003), Meyer et al. (2003), Modell et al. (1998), Wyatt et al. (1998) |
| Chi-squared test adjusted for cluster randomisation. | Meyer et al. (2003) |
| Mixed model anova | Elley et al. (2003), Nutbeam et al. (1993) |
| Generalised estimating equations | Christian et al. (2003), English et al. (2003), Glasgow et al. (2003), Toroyan et al. (2003) |
| Conditional logistic regression | Coulthard et al. (2003) |
| "survey" commands in Stata 7.0 | Smeeth et al. (2003) |
| Corrected for clustering using Stata | Kinmonth et al. (1998), Moore et al. (2003) |
| 95% confidence intervals using a method appropriate for cluster randomised trials | Meyer et al. (2003) |
Thanks to Suezann Puffer, David Torgerson, Sandra Eldridge, Doug Altmann, and Janet Peacock for help with material for this talk.
Addington-Hall JM, Macdonald LD, Anderson HR, Chamberlain J, Freeling P, Bland JM, Raftery J. (1992) A randomised controlled trial of the effects of coordinating care for terminally ill cancer patients. British Medical Journal 305, 1317-1322.
Cornfield J. (1978) Randomisation by group: A formal analysis. American Journal of Epidemiology 108, 100-102.
Donner A. (1982) An empirical-study of cluster randomization. International Journal of Epidemiology 11, 283-286.
Donner A, Birkett N, Buck C. (1981) Randomization by cluster - sample-size requirements and analysis. American Journal of Epidemiology 114, 906-914.
Donner A, Brown KS, Brasher P. (1990) A methodological review of non-therapeutic intervention trials employing cluster randomization, 1979-1989. International Journal of Epidemiology 19, 795-800.
Donner A, Klar N. (2000) Design and Analysis of Cluster Randomised Trials in Health Research. London, Arnold.
Duffy SW, Tabar L, Vitak B, Yen MF, Warwick J, Smith RA, Chen HH. (2003) The Swedish Two-County Trial of mammographic screening: cluster randomisation and end point evaluation. Annals of Oncology 14, 1196-1198.
Eldridge SM, Deborah Ashby, Feder GS, Rudnicka AR Ukoumunne OC. (2003) Lessons for cluster randomised trials in the 21st century: a systematic review of trials in primary care. Clinical Trials, in press.
Hildebrand P, Meyer-Wyss BM, Mossi S, Beglinger C. (2000) Risk among gastroenterologists of acquiring Helicobacter pylori infection: case-control study. British Medical Journal 321, 149.
Kroeger A, Avila EC, Morison, L. (2002) Insecticide impregnated curtains to control domestic transmission of cutaneous leishmaniasis in Venezuela: cluster randomised trial. British Medical Journal 325, 810-813.
Murray (1998) The Design and Analysis of Group-Randomized Trials. Oxford, University Press.
Puffer S, Torgerson D, Watson J. (2003) Evidence for risk of bias in cluster randomised trials: review of recent trials published in three general medical journals. British Medical Journal 327, 785-789.
Simpson JM, Klar N, Donner A. (1995) Accounting for cluster randomization - a review of primary prevention trials, 1990 through 1993. American Journal Of Public Health 85, 1378-1383.
Tabar L and Gad A. (1981) Screening for breast cancer: the Swedish trial. Radiology 138 219-22.
Tabar l, Gad A, Holmberg LH, Ljungquist U, Eklund G, Fagerberg CJG, Baldetorp L, Grontoft O, Lundstrom B, Manson JC, Day NE, Pettersson F. (1985) Reduction in mortality from breast cancer after mass screening with mammography. Lancet i, 829-832.
Christian P, Khatry SK, Katz J, Pradhan EK, LeClerq SC, Shrestha SR, Adhikari RK, Sommer A,West KP. (2003) Effects of alternative maternal micronutrient supplements on low birth weight in rural Nepal: double blind randomised community trial. British Medical Journal 326, 571-574
Coulthard MG, Vernon SJ, Lambert HJ, Matthews JNS.. (2003) A nurse led education and direct access service for the management of urinary tract infections in children: prospective controlled trial. British Medical Journal 327, 656-659.
Elley CR, Kerse N, Arroll B, Robinson E. (2003) Effectiveness of counselling patients on physical activity in general practice: cluster randomised controlled trial. British Medical Journal 326, 793-796.
Emslie C, Grimshaw J, Templeton A. (1993) Do clinical guidelines improve general-practice management and referral of infertile couples? British Medical Journal 306, 1728-1731.
English DR, Burton RC, del Mar CB, Donovan RJ, Ireland PD, Emery G. (2003) Evaluation of aid to diagnosis of pigmented skin lesions in general practice: controlled trial randomised by practice. British Medical Journal 327, 375-378.
Glasgow NJ, Ponsonby A-L, Yates R, Beilby J, Dugdale P. (2003) Proactive asthma care in childhood: general practice based randomised controlled trial British Medical Journal 327, 659-663.
Kinmonth AL, Woodcock A, Griffin S, Spiegal N, Campbell MJ. (1998) Randomised controlled trial of patient centred care of diabetes in general practice: impact on current wellbeing and future disease risk. British Medical Journal 317, 1202-1208.
Meyer G, Warnke A, Bender R, Muhlhauser I. (2003) Effect on hip fractures of increased use of hip protectors in nursing homes: cluster randomised controlled trial. British Medical Journal 326, 76-78.
Modell M, Wonke B, Anionwu E, Khan M, Tai SS, Lloyd M, Modell B. (1998) A multidisciplinary approach for improving services in primary care: randomised controlled trial of screening for haemoglobin disorders. British Medical Journal 317, 788-791.
Moore H, Summerbell CD, DC Greenwood, Tovey P, Griffiths J, Henderson M, Hesketh K, Woolgar S, Adamson AJ. (2003) Improving management of obesity in primary care: cluster randomised trial. British Medical Journal 327, 1085 -
Nutbeam D, Macaskill P, Smith C, Simpson JM, Catford J. (1993) Evaluation of 2 school smoking education-programs under normal classroom conditions. British Medical Journal 306, 102-107.
Rink E, Hilton S, Szczepura A, Fletcher J, Sibbald B, Davies C, Freeling P, Stilwell J. (1993) Impact of introducing near patient testing for standard investigations in general-practice. British Medical Journal 307, 775-778.
Russell MAH, Merriman R, Stapleton J, Taylor W. (1983) Effect of nicotine chewing gum as an adjunct to general-practitioners advice against smoking. British Medical Journal 287, 1782-1785.
Smeeth L, Fletcher AE, Hanciles S, Evans J, Wormald R. (2003) Screening older people for impaired vision in primary care: cluster andomised trial. British Medical Journal 327, 1027-.
Toroyan T, Roberts I, Oakley A, Laing G, Mugford M, Frost C. (2003) Effectiveness of out-of-home day care for disadvantaged families: randomised controlled trial. British Medical Journal 327, 906-909.
Wetsteyn JCFM, Degeus A. (1993) Comparison of 3 regimens for malaria prophylaxis in travelers to East, Central, and Southern Africa. British Medical Journal 307, 1041-1043.
Wright CM, Callum J, Birks E, Jarvis S. (1998) Effect of community based management in failure to thrive: randomised controlled trial. British Medical Journal 317, 571-574.
Wyatt JC, Paterson-Brown S, Johanson R, Altman DG, Bradburn MJ, Fisk NM. (1998) Randomised trial of educational visits to enhance use of systematic reviews in 25 obstetric units. British Medical Journal 317, 1041-1046.
Back to survey of BMJ
Back to Martin Bland's Home Page.
This page is maintained by Martin Bland.
Last updated: 12 January, 2005.