Simple diffraction patterns

There are now two additional views to look at.

Top right is the diffraction pattern. If you rotate the crystal from -45 to +45°, diffraction spots will start to appear here. The vertical axis is the same as the vertical axis in the Bragg diagram, so as we move up or down we are looking at different angles of diffraction. The horizontal axis in this diagram is coming out of the screen in the Bragg diagram, so we don't see this dimension in the other diagrams.
You can clear the diffraction button with the 'clear' button - this is equivalent to starting a new diffraction image. We take multiple diffraction images to get all of the diffraction spots.

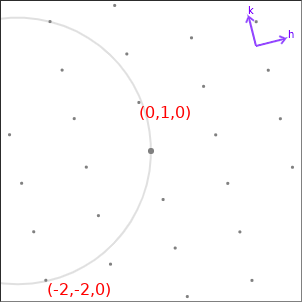
Bottom right is the Ewald sphere construction. This shows the Ewald sphere, along with the reciprocal lattice, rotated to the same orientation as the crystal. As you rotate the crystal, reciprocal lattice points will cross the edge of the sphere. When this happens, the Bragg condition is fulfilled (i.e. the scattered waves are in phase), and so a diffraction spot will appear in the central column of the diffraction pattern. Other spots appear when they cross the sphere in the third dimension, but we cannot see them in this view.
You should be able to see that for the h=0 reciprocal lattice points the waves in the Bragg diagram are in phase when the point crosses the Ewald sphere. For other (h≠0) points, we would have to look at the appropriate set of Bragg planes to see the waves line up - the applet cannot show this, but you could try and draw the relevant condition.

Diffraction spots are only produced when a reciprocal lattice point crosses the Ewald sphere, so in general we need to rotate the crystal in order to produce a diffraction image. For real crystals, this rotation can be small - a few degrees or less. This is called 'precession', and the resulting diffraction pattern is called a 'precession image'. In practice, divergence of the X-ray beam and imperfections in the crystal mean that the reciprocal lattice points are slightly spread, and so we do see a handful of spots even without precession but generally not enough to be useful. The precession angle is chosen to capture a good number of spots but not so many that the spots overlap.

Produce a diffraction image by rotating the crystal from 0° to 25° (i.e. rotate to 0°, click 'clear', and then rotate to 25°). You should get a diffraction pattern like the one shown below.

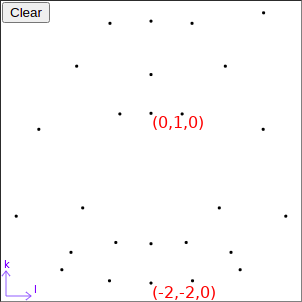
You should be able to identify the Miller indices of the reflections in the central (l=0) column, by watching when the corresponding points in the reciprocal lattice cross the Ewald sphere as you rotate the crystal. (You may have to clear the diffraction pattern and rotate the crystal slowly). I have labelled two of the diffraction spots, and identified them in the reciprocal lattice in the image below. Can you label the other three l=0 spots?