Question 4: Create a new variable to represent an interaction between age and height in their effects on strength. Add the interaction term to the regression.
We use Transform, Compute, to create a new variable htage = height * age.
Click Analyze, Regression, Linear. Select Quadriceps strength into Dependent and Height, Age, and htage into Independents(s). Click OK.
The fourth table of output gives the results:
| Coefficients(a) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Model | Unstandardized Coefficients | Standardized Coefficients | t | Sig. | 95% Confidence Interval for B | |||
| B | Std. Error | Beta | Lower Bound | Upper Bound | ||||
| 1 | (Constant) | 4660.880 | 1781.580 | 2.616 | .013 | 1051.056 | 8270.704 | |
| Height (cm) | -24.736 | 10.439 | -1.440 | -2.370 | .023 | -45.888 | -3.585 | |
| Age (years) | -112.751 | 37.067 | -11.385 | -3.042 | .004 | -187.857 | -37.645 | |
| htage | .647 | .219 | 10.617 | 2.961 | .005 | .204 | 1.090 | |
| a. Dependent Variable: Quadriceps strength (newtons) | ||||||||
The interaction term is highly significant, P = 0.005, so there is strong evidence for an interaction.
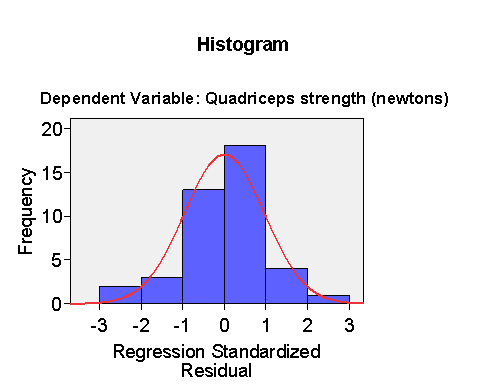
The (edited) residual plots look much better:

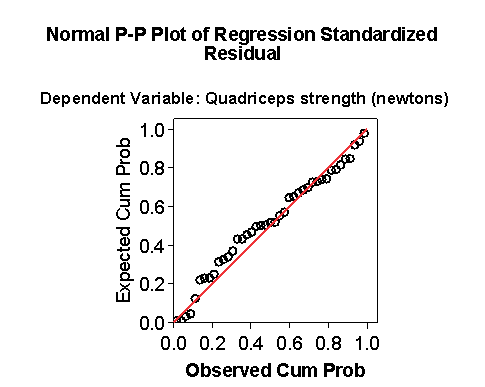
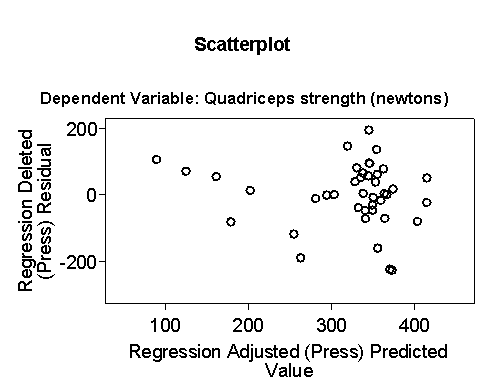
The distribution is less skew and the plot of residual against predicted does not appear to show a relationship.
This regression model appears to be a much better fit to the data.
Back to Exercise: Multiple regression of muscle strength on age and height.
To Applied Biostatistics index.
To Martin Bland's M.Sc. index.
This page maintained by Martin Bland.
Last updated: 19 December, 2006.