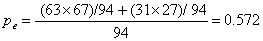
Table 1 shows answers to the question ‘Have you ever smoked a cigarette?’ Obtained from a sample of children on two occasions, using a self administered questionnaire and an interview.
| Self-administered questionnaire | Interview | Total | |
|---|---|---|---|
| Yes | No | ||
| Yes | 61 | 2 | 63 |
| No | 6 | 25 | 31 |
| Total | 67 | 27 | 94 |
We would like to know how closely the children’s answers agree.
One possible method of summarizing the agreement between the pairs of observations is to calculate the percentage of agreement, the percentage of subjects observed to be the same on the two occasions. For Table 1, the percentage agreement is 100×(61+25)/94 = 91.5%. However, this method can be misleading because it does not take into account the agreement which we would expect even if the two observations were unrelated.
Consider Table 2, which shows some artificial data relating observations by one observer to those by two others.
| Observer A | Observer B | Total | |
|---|---|---|---|
| Yes | No | ||
| Yes | 10 | 10 | 20 |
| No | 10 | 70 | 80 |
| Total | 20 | 80 | 100 |
| Observer A | Observer C | Total | |
|---|---|---|---|
| Yes | No | ||
| Yes | 0 | 20 | 20 |
| No | 0 | 80 | 80 |
| Total | 0 | 100 | 100 |
For Observers A and B, the percentage agreement is 80%, as it is for Observers A and C. This would suggest that Observers B and C are equivalent. However, Observer C always chooses ‘No’. Because Observer A chooses ‘No’ often they appear to agree, but in fact they are using different and unrelated strategies for forming their opinions.
Table 3 shows further artificial agreement data.
| Observer A | Observer D | Total | |
|---|---|---|---|
| Yes | No | ||
| Yes | 4 | 16 | 20 |
| No | 16 | 64 | 80 |
| Total | 20 | 80 | 100 |
Observers A and D give ratings which are independent of one another, the frequencies in Table 3 being equal to the expected frequencies under the null hypothesis of independence (chi-squared = 0.0). The percentage agreement is 68%, which may not sound very much worse than 80% for Table 3. However, there is no more agreement than we would expect by chance. The proportion of subjects for which there is agreement tells us nothing at all. To look at the extent to which there is agreement other than that expected by chance, we need a different method of analysis: Cohen’s kappa.
Percentage agreement is widely used, but may be highly misleading. For example, Barrett et al. (1990) reviewed the appropriateness of caesarean section in a group of cases, all of whom had had a section due to of fetal distress. They quoted the percentage agreement between each pair of observers in their panel. These varied from 60% to 82.5%. If they made their decisions at random, with an equal probability for ‘appropriate’ and ‘inappropriate’, the expected agreement would be 50%. If they tended to rate a greater proportion as ‘appropriate’ this would be higher, e.g. if they rated 80% ‘appropriate’ the agreement expected by chance would be 68% (0.8×0.8 + 0.2×0.2 = 0.68). As noted by Esmail and Bland (1990), in the absence of the percentage classified as ‘appropriate’ we cannot tell whether their ratings had any validity at all.
Cohen’s kappa (Cohen 1960) was introduced as a measure of agreement which avoids the problems described above by adjusting the observed proportional agreement to take account of the amount of agreement which would be expected by chance.
First we calculate the proportion of units where there is agreement, p, and the proportion of units which would be expected to agree by chance, pe. The expected numbers agreeing are found as in chi-squared tests, by row total times column total divided by grand total. For Table 1, for example, we get
p = (61 + 25)/94 = 0.915
and
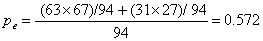
Cohen’s kappa (κ) is then defined by
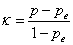
For Table 1 we get:
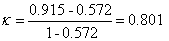
Cohen’s kappa is thus the agreement adjusted for that expected by chance. It is the amount by which the observed agreement exceeds that expected by chance alone, divided by the maximum which this difference could be.
Kappa distinguishes between the tables of Tables 2 and 3 very well. For Observers A and B, κ = 0.37, whereas for Observers A and C κ = 0.00, as it does for Observers A and D.
We will have perfect agreement when all agree, so p = 1. For perfect agreement κ = 1. We may have no agreement in the sense of no relationship, when p = pe and so κ = 0. We may also have no agreement when there is an inverse relationship. In Table 1, this would be if children who said 'no' the first time said 'yes' the second and vice versa. We would have p < pe and so κ < 0.
The lowest possible value for κ is –pe/(1 – pe), so depending on pe, κ may take any negative value. Thus κ is not like a correlation coefficient, lying between –1 and +1. Only values between 0 and 1 have any useful meaning. As Fleiss showed, kappa is a form of intra-class correlation coefficient.
| Self-administered questionnaire | Interview | Total | ||
|---|---|---|---|---|
| Yes | No | Don’t know | ||
| Yes | 12 | 4 | 2 | 18 |
| No | 12 | 56 | 0 | 68 |
| Don’t know | 3 | 4 | 1 | 7 |
| Total | 27 | 64 | 3 | 94 |
| Self-administered questionnaire | Interview | Total | |
|---|---|---|---|
| Yes | No/DK | ||
| Yes | 12 | 6 | 18 |
| No/DK | 15 | 61 | 76 |
| Total | 27 | 67 | 94 |
Table 4 shows three categories, ‘yes’, ‘no’ and ‘don’t know’, and Table 5 shows two categories, ‘no’ and ‘don’t know’ being combined into a ‘negative’ group. For Table 4, p = 0.73, pe = 0.55, κ = 0.41. For Table 5, p = 0.78, pe = 0.63, κ = 0.39.
The proportion agreeing, p, increases when we combine the ‘no’ and ‘don’t know’ categories, but so does the expected proportion agreeing pe. Hence κ does not necessarily increase because the proportion agreeing increased. Whether it does so depends on the relationship between the categories. When the probability that an incorrect judgment will be in a given category does not depend on the true category, kappa tends to go down when categories are combined. When categories are ordered, so that incorrect judgments tend to be in the categories on either side of the truth, and adjacent categories are combined, kappa tends to increase.
For example, Table 6 shows the agreement between two ratings of physical health, obtained from a sample of mainly elderly stoma patients.
| General Practitioner | Health Visitor | Total | |||
|---|---|---|---|---|---|
| Poor | Fair | Good | Excellent | ||
| Poor | 2 (1.1) | 12 (5.5) | 8 (11.4) | 0 (4.1) | 22 |
| Fair | 9 (4.1) | 35 (23.4) | 43 (48.8) | 7 (17.7) | 94 |
| Good | 4 (8.0) | 36 (45.5) | 103 (95.0) | 40 (34.5) | 83 |
| Excellent | 1 (2.9) | 8 (16.7) | 36 (36.8) | 22 (12.6) | 67 |
| Total | 16 | 91 | 190 | 69 | 366 |
| p = 0.443, pe = 0.361, κ = 0.13 | |||||
The analysis was carried out to see whether self reports could be used in surveys. For these data, κ = 0.13. If we combine the categories ‘poor’ and ‘fair’ we get κ = 0.19. If we then combine categories ‘good’ and ‘excellent’ we get κ = 0.31. Thus kappa increases as we combine adjoining categories. Data with ordered categories are better analysed using weighted kappa, described below.
| Morning cough, two weeks | 0.62 |
| Day or night cough, two weeks | 0.41 |
| Morning cough, since Christmas | 0.24 |
| Day or night cough, since Christmas | 0.10 |
| Ever smoked | 0.80 |
| Smokes now | 0.82 |
The kappa values show a clear structure to the questions. The questions on smoking have clearly better agreement than the respiratory questions. Among the latter, the recent period is more consistently answered than the time since Christmas, and morning cough is more consistently than day or night cough. Here the kappa statistics are quite informative.
How large should kappa be to indicate good agreement? This is a difficult question, as what constitutes good agreement will depend on the use to which the assessment will be put. Kappa is not easy to interpret in terms of the precision of a single observation. The problem is the same as arises with correlation coefficients for measurement error in continuous data. Table 8 gives guidelines for its interpretation, slightly adapted from Landis and Koch (1977).
| Value of kappa | Strength of agreement |
|---|---|
| <0.20 | Poor |
| 0.21-0.40 | Fair |
| 0.41-0.60 | Moderate |
| 0.61-0.80 | Good |
| 0.81-1.00 | Very good |
This is only a guide, and does not help much when we are interested in the clinical meaning of an assessment.
The standard error of κ is given by
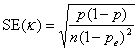
where n is the number of subjects.
The 95% confidence interval for κ is κ – 1.96×SE(κ) to κ + 1.96×SE(κ) as κ is approximately Normally Distributed, provided np and n(1 – p) are large enough, say greater than five.
For the data of Table 1:
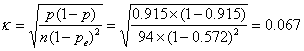
For the 95% confidence interval we have: 0.801 – 1.96×0.067 to 0.801+1.96×0.067 = 0.67 to 0.93.
We can also carry out a significance test of the null hypothesis of no agreement. The null hypothesis is that in the population κ = 0, or p = pe. This affects the standard error of kappa because the standard error depends on p, in the same way that it does when comparing two proportions (Bland, 2000, p 145-7).
Under the null hypothesis, p can be replaced by pe in the standard error formula:
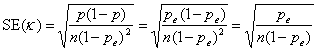
If the null hypothesis were true, κ/SE(κ) would be from a Standard Normal Distribution. For the example, κ/SE(κ) = 6.71, P < 0.0001. This test is one tailed, as zero and all negative values of κ mean no agreement.
Because the confidence interval and the significance test use different standard errors, it is possible to get a significant difference when the confidence interval contains zero. In this case there is evidence of some agreement, but kappa is poorly estimated.
There are problems in the interpretation of kappa. To illustrate them, I am going to do a bit of maths. I do not mind at all if you just accept that I can do it and skip a few paragraphs.
Kappa depends on the proportions of subjects who have true values in each category. To show this, suppose we have two categories, and the proportion in the first category is p1. The probability that an observer is correct is q, and we shall assume that the probability of a correct assessment is unrelated to the subject’s true status. This is a very strong assumption, but it makes the demonstration easier.
We have observations by two observers on a group of subjects. Observers will agree if they are both right, which happens with probability q×q = q2, and if they are both wrong, which has probability (1 – q)×(1 – q) = (1 – q)2. Then the proportion of pairs of observations which agree is q2 + (1 – q)2.
The proportion of subjects judged to be in category one by an observer will be p1q + (1 – p1)(1 – q), i.e. the proportion truly in category one times the probability that the observer is right plus the proportion truly in category two times the probability that the observer will be wrong. Similarly, the proportion in category two will be p1(1 – q) + (1 – p1)q.
Thus the expected chance agreement will be:
pe = [p1q + (1 – p1) (1 – q)]2 + [p1(1 – q) + (1 – p1)q)]2 = q2 + (1 – q)2 – 2(1 – 2q)2p1(1 – p).
This gives us for kappa:
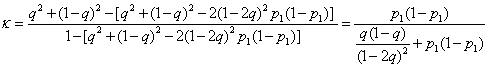
Inspection of this equation shows that unless q = 1 or 0.5, all observations always correct when or random assessments, kappa depends on p1, having a maximum when p1 = 0.5. Thus kappa will be specific for a given population. This is like the intra-class correlation coefficient, to which kappa is related, and has the same implications for sampling. If we choose a group of subjects to have a larger number in rare categories than does the population we are studying, kappa will be larger in the observer agreement sample than it would be in the population as a whole. Figure 1 shows the predicted two-category kappa against the proportion who are ‘yes’ for different probabilities that the observer’s assessment will be correct.
Figure 1. Predicted kappa for two categories, ‘yes’ and ‘no’,
by probability of a ‘yes’ and probability observer will be correct.
The verbal categories of Landis and Koch are shown.
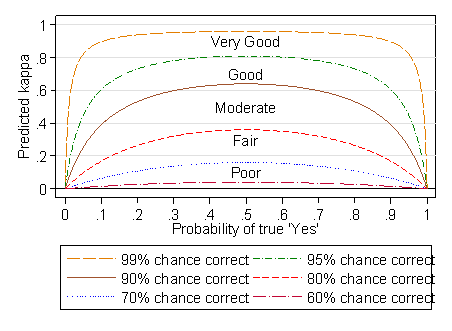
What is most striking about Figure 1 is that kappa is maximum when the probability of a true 'yes' is 0.5. As this probability gets closer to zero or to one, the expected kappa gets smaller, quite dramatically so at the extremes when agreement is very good. Unless the agreement is perfect, if one of two categories is small compared to the other, kappa will be small, no matter how good the agreement is. This causes grief for a lot of users.
We can see that the lines in Figure 1 correspond quite closely to the categories of Landis and Koch, shown in Table 8.
For the data of Table 6, kappa is low, 0.13. However, this may be misleading. Here the categories are ordered. The disagreement between ‘good’ and ‘excellent’ is not as great as between ‘poor’ and ‘excellent’. We may think that a difference of one category is reasonable whereas others are not. We can take this into account if we allocate weights to the importance of disagreements, as shown in Table 9.
| General Practitioner | Health Visitor | |||
|---|---|---|---|---|
| Poor | Fair | Good | Excellent | |
| Poor | 0 | 1 | 2 | 3 |
| Fair | 1 | 0 | 1 | 2 |
| Good | 2 | 1 | 0 | 1 |
| Excellent | 3 | 2 | 1 | 2 |
We suppose that the disagreement between ‘Poor’ and ‘Excellent’ is three times that between ‘Poor’ and ‘Fair’. As the weight is for the degree of disagreement, a weight of zero means that observations in this cell agree.
Now for another little mathematical diversion, which you could skip. Denote the weight for cell in row i and column j (cell i,j) by wij, the proportion in cell i,j by pij, and the expected proportion in cell i,j by pe,ij. The weighted disagreement will be found by multiplying the proportion in each cell by its weight and adding, Σwijpij. We can turn this into a weighted proportion disagreeing by dividing by the maximum weight, wmax,. This is the largest value which Σwijpij can take, attained when all observations are in the cell with the largest weight. The weighted proportion agreeing would be one minus this. Thus the weighted proportion agreeing is p = 1 – Σwijpij/wmax,. Similarly, the weighted expected proportion agreeing is pe = 1 – Σwijpe,ij/wmax,. .
Defining weighted kappa as for standard kappa, we get
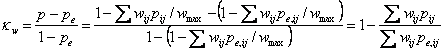
If all the wij = 1 except on the main diagonal, where wii = 0, we get the usual unweighted kappa.
For Table 6, using the weights of Table 9, we get κw = 0.23, larger than the unweighted value of 0.13.
The standard error of weighted kappa is given by the approximate formula:
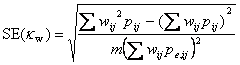
For the significance test this reduces to
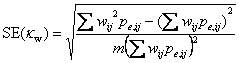
by replacing the observed pij by their expected values under the null hypothesis. We use these as we did for unweighted kappa.
The choice of weights is important. If we define a new set, the squares of the old, as shown in Table 10, we get κw = 0.35.
| General Practitioner | Health Visitor | |||
|---|---|---|---|---|
| Poor | Fair | Good | Excellent | |
| Poor | 0 | 1 | 4 | 9 |
| Fair | 1 | 0 | 1 | 4 |
| Good | 4 | 1 | 0 | 1 |
| Excellent | 9 | 2 | 1 | 2 |
In the example, the agreement is better if we attach a bigger relative penalty to disagreements between ‘poor’ and ‘excellent’. Clearly, we should define these weights in advance rather than derive them from the data. Cohen (1968) recommended that a committee of experts decide them, but in practice it seems unlikely that this happens. In any case, when using weighted kappa we should state the weights used. I suspect that in practice people use the default weights of the program.
If we combine categories, weighted kappa may still change, but it should do so to a lesser extent than unweighted kappa. We should state the weights which are used for weighted kappa.
The weights in Table 9 are sometimes called linear weights. Linear weights are proportional to number of categories apart. The weights in Table 10 are sometimes called quadratic weights. Quadratic weights are proportional to the square of the number of categories apart.
Table 9 and Table 10 show weights as originally defined by Cohen (1968). It is also possible to describe the weights as weights for the agreement rather than the disagreement. This is what Stata does. (SPSS 16 does not do weighted kappa.) Stata would give the weight for perfect agreement along the main diagonal (i.e. “poor” and “poor”, “fair” and “fair”, etc.) as 1.0. It then gives smaller weights for the other cells, the smallest weight being for the biggest disagreement (i.e. “poor” and “excellent”). Table 11 shows linear weights for agreement rather than for disagreement, standardised so that 1.0 is perfect agreement.
| General Practitioner | Health Visitor | |||
|---|---|---|---|---|
| Poor | Fair | Good | Excellent | |
| Poor | 1.00 | 0.67 | 0.33 | 0.00 |
| Fair | 0.67 | 1.00 | 0.67 | 0.33 |
| Good | 0.33 | 0.67 | 1.00 | 0.67 |
| Excellent | 0.00 | 0.33 | 0.67 | 1.00 |
Like Table 9, in Table 11 the weights are equally spaced, going down to zero. To get the weights for agreement from those for disagreement, we subtract the disagreement weights from their maximum value and divide by that maximum value. For the quadratic weights of Table 10, we get the quadratic weights for agreement shown in Table 12.
| General Practitioner | Health Visitor | |||
|---|---|---|---|---|
| Poor | Fair | Good | Excellent | |
| Poor | 1.00 | 0.89 | 0.56 | 0.00 |
| Fair | 0.89 | 1.00 | 0.89 | 0.56 |
| Good | 0.56 | 0.89 | 1.00 | 0.89 |
| Excellent | 0.00 | 0.56 | 0.89 | 1.00 |
Both versions of linear weights give the same kappa statistic, as do both versions of quadratic weights.
| Statement | Observer | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | H | I | J | |
| 1 | C | C | C | C | C | C | C | C | C | C |
| 2 | P | C | C | C | C | P | C | C | C | C |
| 3 | A | C | C | C | C | P | P | C | C | C |
| 4 | P | A | A | A | P | A | C | C | C | C |
| 5 | A | A | A | A | P | A | A | A | A | P |
| 6 | C | C | C | C | C | C | C | C | C | C |
| 7 | A | A | A | A | P | A | A | A | A | A |
| 8 | C | C | C | C | A | C | P | A | C | C |
| 9 | P | P | P | P | P | P | P | A | P | P |
| 10 | P | P | P | P | P | P | P | P | P | P |
| 11 | P | C | C | C | C | P | C | C | C | C |
| 12 | P | P | P | P | P | P | A | C | C | P |
| 13 | P | A | P | P | P | A | P | P | A | A |
| 14 | C | P | P | P | P | P | P | C | A | P |
| 15 | A | A | P | P | P | C | P | A | A | C |
| 16 | P | A | C | P | P | A | C | C | C | C |
| 17 | P | P | C | C | C | C | P | A | C | C |
| 18 | C | C | C | C | C | A | P | C | C | C |
| 19 | C | A | C | C | C | A | C | A | C | C |
| 20 | A | C | P | C | P | P | P | A | C | P |
| 21 | C | C | C | P | C | C | C | C | C | C |
| 22 | A | A | C | A | P | A | C | A | A | A |
| 23 | P | P | P | P | P | A | P | P | P | P |
| 24 | P | C | P | C | C | P | P | C | P | P |
| 25 | C | C | C | C | C | C | C | C | C | C |
| 26 | C | C | C | C | C | C | C | C | C | C |
| 27 | A | P | P | A | P | A | C | C | A | A |
| 28 | C | C | C | C | C | C | C | C | C | C |
| 29 | A | A | C | C | A | A | A | A | A | A |
| 30 | A | A | C | A | P | P | A | P | A | A |
| 31 | C | C | C | C | C | C | C | C | C | C |
| 32 | P | C | P | P | P | P | C | P | P | P |
| 33 | P | P | P | P | P | P | P | P | P | P |
| 34 | P | P | P | P | A | C | C | A | C | C |
| 35 | P | P | P | P | P | A | P | P | A | P |
| 36 | P | P | P | P | P | P | P | C | C | P |
| 37 | A | C | P | P | P | P | P | P | C | A |
| 38 | C | C | C | C | C | C | C | C | C | P |
| 39 | A | C | C | C | C | C | C | C | C | C |
| 40 | A | P | C | A | A | A | A | A | A | A |
Observers watched video recordings of discussions between anorexic subjects and their families. Observers classified 40 statements as being made by ‘adult’, ‘parent’ or ‘child’, as a way of understanding the psychological relationships between the family members. For some statements, such as statement 1, there was perfect agreement, all observers giving the same classification. Others statements, e.g. statement 15, produced no agreement between the observers. These data were collected as a validation exercise, to see whether there was any agreement at all between observers. In this section, we extend kappa to more than two observers.
Fleiss (1971) extended Cohen’s kappa to the study of agreement between many observers. To estimate kappa by Fleiss’ method we ignore any relationship between observers for different subjects. This method does not take any weighting of disagreements into account, and so is suitable for the data of Table 13.
We shall omit the details. For Table 13, κ = 0.43.
Fleiss only gives the standard error of kappa for testing the null hypothesis of no agreement. For Table 13 it is SE(κ) = 0.02198. If the null hypothesis were true, the ratio κ/SE(κ) would be from a Standard Normal Distribution; κ/SE(κ) = 0.43156/0.02198 = 19.6, P < 0.001. The agreement is highly significant and we can conclude that transactional analysts assessments are not random.
Fleiss only gives the standard error of kappa for many observers under the null hypothesis. The distribution of kappa if there is agreement is not known, which means that confidence intervals and comparison of kappa statistics can only be approximate.
We can extend Fleiss’s method to the case when the number of observers is not the same for each subject but varies, and for weighted kappa.
Barrett, J.F.R., Jarvis, G.J., Macdonald, H.N., Buchan, P.C., Tyrrell S.N., and Lilford, R.J. (1990) Inconsistencies in clinical decision in obstetrics. Lancet 336, 549-551.
Cohen, J. (1960) A coefficient of agreement for nominal scales. Educational and Psychological Measurement 20, 37-46.
Cohen, J. (1968) Weighted kappa: nominal scale agreement with provision for scaled disagreement or partial credit. Psychological Bulletin 70, 213-220.
Esmail, A. and Bland, M. (1990) Caesarian section for fetal distress. Lancet 336, 819.
Falkowski, W., Ben-Tovim, D.I., and Bland, J.M. (1980) The assessment of the ego states. British Journal of Psychiatry 137, 572-573.
Fleiss, J.L. (1971) Measuring nominal scale agreement among many raters. Psychological Bulletin 76, 378-382.
Landis, J.R. and Koch, G.G. (1977) The measurement of observer agreement for categorical data. Biometrics 33, 159-74.
To Measurement in Health and Disease index.
To Martin Bland's M.Sc. index.
This page maintained by Martin Bland.
Last updated: 22 July, 2008.