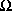- baryon, was accomplished with the observation of a single isolated quantum event.
Go back to Table of Contents
Go back to Appendices
Continue on to Figures
1. There have been several attempts in the literature to answer the question: "What is the minimum assumption about the physical world which one must relinquish in order to retain the locality assumption in the face of the Bell Inequality experimental results?" D'Espagnat (1976, 1979) has suggested that the minimum assumption is the existence of an objective external reality which is independent of the knowledge of observers. Clauser and Shimony (1978) have suggested the slightly weaker assumption of "realism", i.e., that external reality exists and has definite objective properties whether we measure them or not. Stapp's (1971) CFD assumption described in the text is, in the opinion of the author, a considerably weaker assumption than others proposed in the literature and is therefore the minimum assumption of choice.
2. Some authors use the terms "separable" and "separability", which are synonymous with "local" and "locality" in the present context.
3. Here we must distinguish between causality in the sense that an effect must follow its cause in time sequence, and causality as used, for example, by Heisenberg (1927) to mean that the effect is completely and uniquely determined by its cause(s). The former concept as applied to macroscopic systems is assumed here to be a valid and fundamental law of nature; the latter concept is presumably invalid because it is in conflict with the statistical interpretation of QM (see Section 2.0). In the present paper we will take causality to have the former meaning and reserve the term determinism to refer to the latter concept.
4. There are experimental predictions associated with the Wheeler-Feynman approach which differ from those of orthodox quantum mechanics, but only for special situations involving very weak and anisotropic absorption (Partridge, 1973; Pegg, 1975; Cramer, 1980, 1983). However, even in the unlikely event that such effects were observed, no revision of the QM formalism would be required. Rather, the same formalism would be used in a slightly different way involving altered boundary conditions for such cases.
5. Some authors (Ballentine, 1970) extend the statistical interpretation further by asserting that the formalism of QM is applicable only to groups of similar events and should not be applied to isolated events. In our opinion this extreme view is unwarranted as long as it is appreciated that the predictivity of the QM formalism is severely limited in its application to isolated events. We note that the discovery of an important particle in the development of particle physics, the 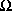- baryon, was accomplished with the observation of a single isolated quantum event.
6. The "our knowledge" element of the CI was not explicitly stated in the early interpretational papers of Bohr and Heisenberg. It apparently played an important role in the general discussion which followed Einstein's criticism of QM at the 5th Solvay Conference in 1927 (Jammer, 1966). It was also clearly articulated in the later writings of Heisenberg (1958b): "The laws of nature which we formulate mathematically in quantum theory deal no longer with the particles themselves but with our knowledge of the elementary particles. ... The conception of objective reality ... evaporated into the ... mathematics that represents no longer the behavior of elementary particles but rather our knowledge of this behavior." (Italics by author.) See also Hartle (1968) and Peierls (1979) for discussions of the "our knowledge" interpretation of the state vector.
7. W. Heisenberg:
"The act of recording, on the other hand, which leads to the reduction of the state, is not a physical, but rather, so to say, a mathematical process. With the sudden change of our knowledge also the mathematical presentation of our knowledge undergoes of course a sudden change.",as translated by Jammer (1974) from a letter to Renninger dated February 2, 1960.
"... it is possible to ask whether there is still concealed behind the statistical universe of perception a 'true' universe in which the law of causality (=determinism) would be valid. But such speculations seem to us to be without value and meaningless, for physics must confine itself to the description of the relationships between perceptions."
9. The strict positivism of CI5 is the most "detachable" element of the CI. It was later softened by many of the proponents of the CI including Heisenberg (1960). For example, consider the statement by Feynman (1965):
"Just because we cannot measure position and momentum precisely does not a priori mean that we cannot talk about them. It only means that we need not talk about them. The situation in the sciences is this: A concept or an idea which cannot be measured or cannot be referred directly to experiment may or may not be useful. It need not exist in a theory."
10. To our list of CI elements some might add Bohr's correspondence principle, the reduction of quantum mechanical predictions to those of classical mechanics in the limit of large principle quantum numbers. In our opinion this is a useful property of the QM formalism rather than an aspect of its interpretation.
11. Schrödinger's visit to Copenhagen in the Summer of 1926 and his discussions with Heisenberg and Bohr over his semiclassical interpretation represented a crucial test in the development of the Copenhagen interpretation. See Jammer (1974), pp. 56-57 and Wheeler (1983), pp. 50-51.
12. In the present paper we will employ the term "collapse of the state vector". Other authors sometimes use the terms "reduction" in place of "collapse" and/or "wave packet" or "wave function" in place of "state vector" with the same meaning. Bohr (1935a, 1935b) employs the term "rupture of description". Von Neumann (1932) describes the phenomenon mathematically with his projection postulate.
13. The formalism of quantum mechanics can predict the outcome of a single isolated quantum event in the unusual circumstance when one particular outcome of the event has a predicted probability of 1.0 and all other outcomes have predicted probabilities of zero. An example is the measurement of a particular variable after the system has been prepared in a unique state of that variable, e.g., transmission of a photon through successive aligned linear polarizers.
14. The account of an emitter-absorber transaction presented here employs the semantic device of describing a process extending across a lightlike or timelike interval of space-time as if it occurred in an time sequence external to the process. The reader is reminded that this is only a pedagogical convention for the purposes of description. The process is atemporal and the only observables come from the superposition of all "steps" to form the final transaction. (See also Appendix A.6 on this point.)
15. The statement that an advanced wave may be reinterpreted as a retarded wave (or vice versa) which is propagating in the opposite direction with sign-reversed energy and frequency is actually a classical oversimplification of the QM formalism. Advanced waves have the characteristic time dependent phase exp(i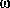
t) while retarded waves have phase exp(-i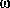t). These functions are orthogonal and in principle distinguishable. Reinterpretation is permissible because it is consistent with the observed transfer of energy, momentum, etc., and because the time phases are not observed.
16. A transaction involving charged particles, particularly in the presence of external electric and magnetic fields, must be more carefully described. To obtain the path of the advanced wave the operation of time reversal must be performed not only on the charged particle SV but also on the external fields which it "sees" as acting along its time-reversed path back to the emitter. The time reversal operation on such electric and magnetic fields must be applied to the proper Lorentz 6-vector describing the electromagnetic field. This has the effect of reversing the signs of (real) magnetic fields while leaving the sign of (real) electric fields unchanged. Since the particle momentum also changes sign under time-reversal, the Lorentz forces act in the same way as on the "forward" particle and the time-reversed particle retraces the path of the former. Clearly there is nothing about the time reversal properties of a magnetic field which causes problems for the transactional model because any system with a uniform external magnetic field can be transformed into a Lorentz frame in which the external field is purely electric.
17. The time dependent Schrödinger equation is an operator-equation version of the non-relativistic kinematics equation p2/2m=E, where p is the momentum and E is the kinetic energy of a particle of mass m. The momentum operator is [
/i]d/dx and the energy operator is [i]d/dt, in that the indicated operations when performed on a quantum mechanical wave function, e.g.,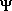 
= Ao × exp[i(k.r-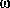t)], yield the unaltered wave function (psi) multiplied by its momentum eigenvalue k or energy eigenvalue 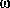. If these operators are substituted in the above kinematic equation the Schrödinger equation results. The equivalent expression for relativistic kinematics is (pc)2 + (mc2)2 = W2, where W is the total mass-energy. The operator equation version of this expression is the Klein-Gordon equation (Bjorken, 1964).
18. See for example Messiah (1961), p. 61, for a clear statement of the widely held supposition that proper QM wave equations should be first order with respect to time so as to uniquely specify the state and the time evolution of the system. See also the discussion of "pathology" of the Klein-Gordon equation in this context on p. 65.
19. Here "transmits" means that the state vector (or offer wave) is split into components which stop at the polarizer and components which continue on the original path. The "transmitted" OW is in the latter class. Thus a transaction involving components which are not transmitted cannot form on the path beyond the polarizer.
20. The net wave at the absorber locus is also real. Assume that in the vicinity of the absorber |V> depends on x and t as |V> = exp[i(kx-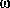t)]. Then <V| = [|V>]* = exp[-i(kx-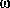t)]. Thus at the absorber locus the net wave is the superposition (i/2)|V>+(-i/2)<V| = -Sin(kx-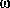t), which is a real quantity.
21. The transmission of the initial photon through the first polarizing filter has not been considered in this calculation. There is a 50% probability that a photon of indefinite polarization would be absorbed by the first filter, giving a net transmission of a beam of photons from the source to the detector of 1/8 rather than 1/4, which is the transmission from the first filter on. It should be emphasized that there is a difference in definition between "unpolarized" in the classical sense and "of indefinite polarization" in the QM sense. This represents a fundamental difference between the QM and classical treatments of polarization and the lack thereof. It is related to the Furry modification of QM discussed in Section 2.4. This difference is not related to the QM interpretation but to the formalism. The latter accommodates randomly polarized light in the classical sense by averaging over polarization orientations.
Continue on to Figures
Go back to Appendices
Go back to Table of Contents