Research
My research goal is to extend the unparalleled success of density functional theory for calculating ground-state properties to the calculation of excited states.
Introduction
Modelling materials using quantum mechanics requires the many-body Schrödinger equation to be solved. However, solving this equation for even moderately large systems is extremely computationally expensive. Therefore, approximations must be used in order to make the calculations possible. These approximations often involve simplifying the problem in some way, for instance, by imposing limitations on the form of the electron wavefunction. The approximations used in density functional theory (DFT) are able to accurately predict the properties of real materials in many cases, but they are notoriously unreliable for modelling excitation processes, which are central to the next generation of technologies.
Electron excitation
Kohn and Sham's approach to DFT is the most widely used method for calculating ground-state electronic properties thanks to its computationally inexpensive approximations that are reliable when the electrons are in their lowest energy state. However, these commonly used approximations are unreliable for modelling excited states.
The Kohn-Sham approach is a powerful methodology that utilises a system of fully non-interacting electrons, which are influenced by an effective external potential. This Kohn-Sham
potential guarantees that the single-particle electron density matches that of the interacting many-body system. By employing this auxiliary system within the framework of DFT, it becomes possible to extract many-body observables from the single-particle system at a significantly reduced computational cost. However, the accuracy of this approach strongly depends the Kohn-Sham effective potential. Approximations have to be utalised to determine this potential for realistic materials, making it less reliable in certain physical situations.
Using our iDEA code, we model prototype systems that mimic the fundamental physics of excitation processes in real materials. By applying iDEA's powerful inversion algorithms, we can study the exact Kohn-Sham potential of the system when electrons are excited. By comparing the exact potential to approximate potentials we can gain the insights needed to develop improved, practical approximations for reliably modelling excitation processes in real materials.
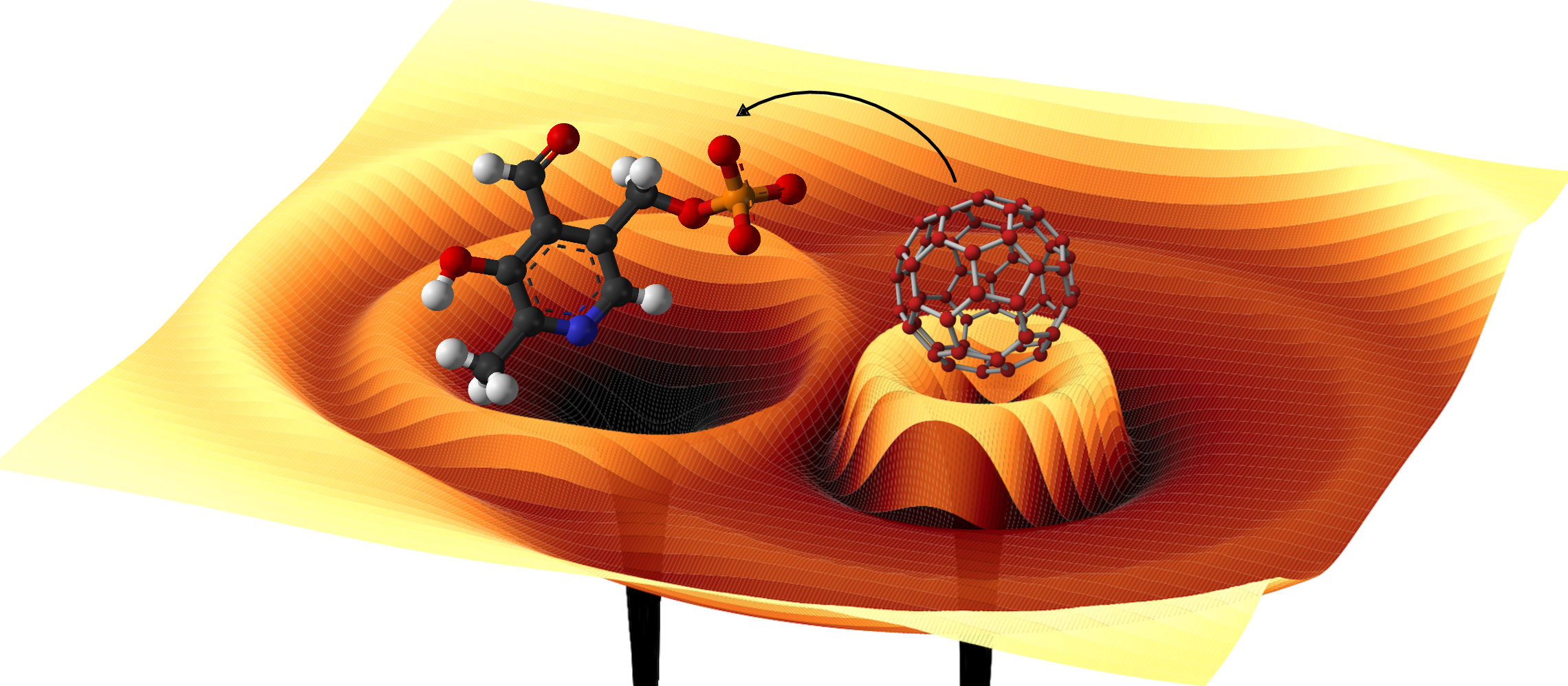
Our research has shown that the Kohn-Sham potential experiences discontinuities when a charge transfer excitation occurs (see publication). We have demonstrated that, in principle, the exact charge-transfer energy can be obtained from the Kohn-Sham system through this discontinuous behaviour. Therefore, by using a sufficiently advanced approximation that is able to capture non-analytic behaviour (see publication), it is possible to accurately calculate the charge-transfer energy. To learn more about obtaining excitation energies from the Kohn-Sham system see the video below.
Electron dynamics
With the advent of experimental techniques sophisticated enough to measure minuscule electron currents within molecular junctions, comes the need for precise models of electron dynamics.
In principle, Kohn-Sham time-dependent density functional theory (TDDFT) can accurately calculate electron currents. However, existing approximations to the Kohn-Sham potential are known to be unreliable in the presence of strong electric fields. This is because the exact time-dependent Kohn-Sham potential depends on the density throughout the entire system and for the system's complete histroy. As a result, when the electrons begin to move due to the electric field, the Kohn-Sham potential in the region of each electron must consider the behavior of all other electrons in the system and each electron's past behaviour. As a result, accurately approximating the time-dependent Kohn-Sham potential can be extremely challenging.
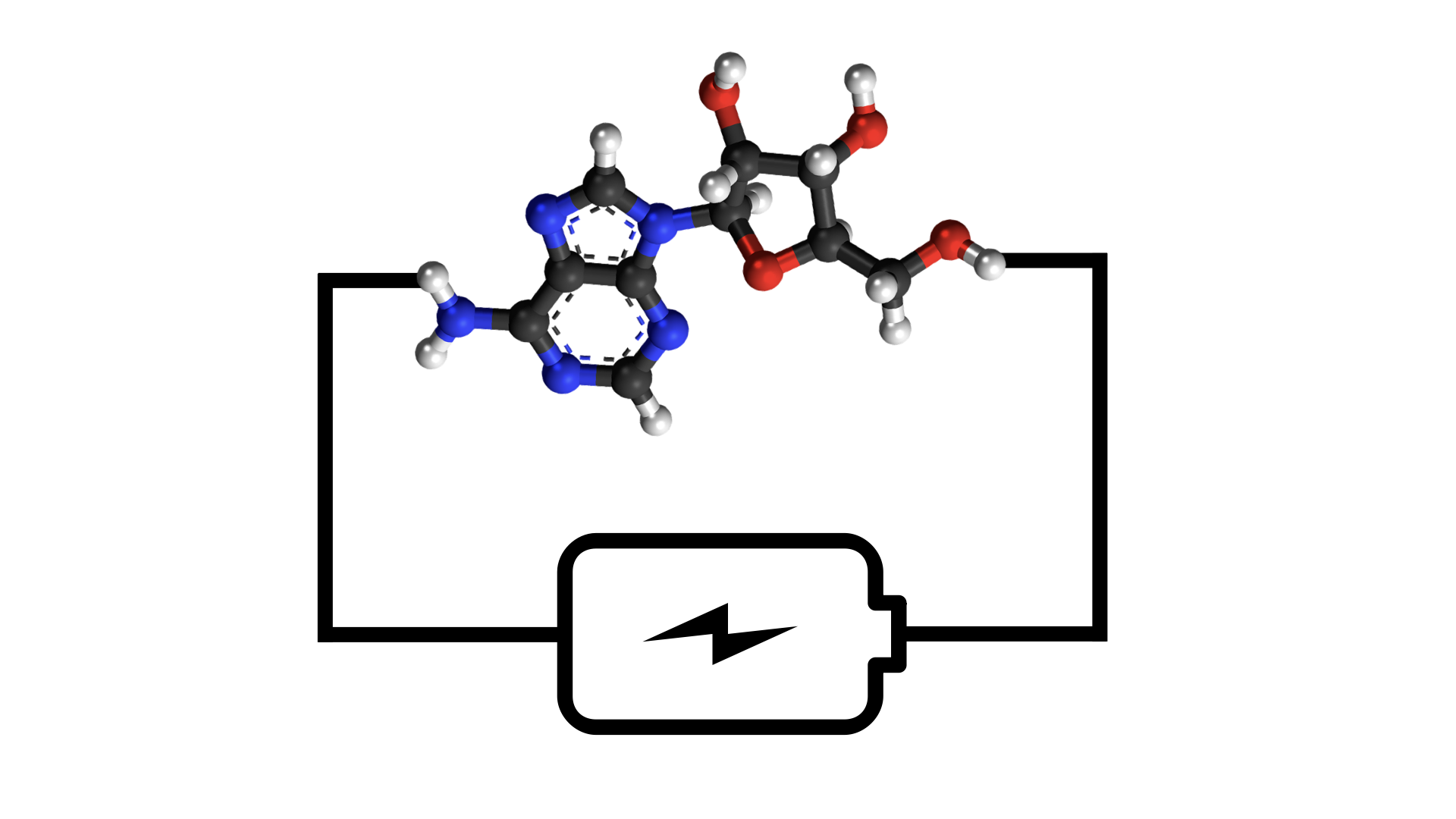
Our research has shown that the flow of electron density (electron current) in the Kohn-Sham system is controlled in part by dynamic potential differences (PDs) that form within the Kohn-Sham potential (see publication). These PDs manifest as steps in the potential (significant changes in potential over a short distance). Importantly, these dynamic features are not captured by commonly used approximations to the time-dependent Kohn-Sham potential which limits the accuracy of the simulation.
We have developed a novel method for accurately and efficiently simulating electron behaviour in molecular junctions within generalised Kohn-Sham theory (see publication). By designing the Kohn-Sham potential to be nearsighted
, we ensure that it is only concerned with the electron density in its immediate surroundings. As a result, our method reduces the reliance of the potential on steps, allowing simple local approximations to this nearsighted potential to be are more effective than approximations to the traditional, strongly non-local Kohn-Sham potential. To learn more about this method, please watch the video below.
Electron emission
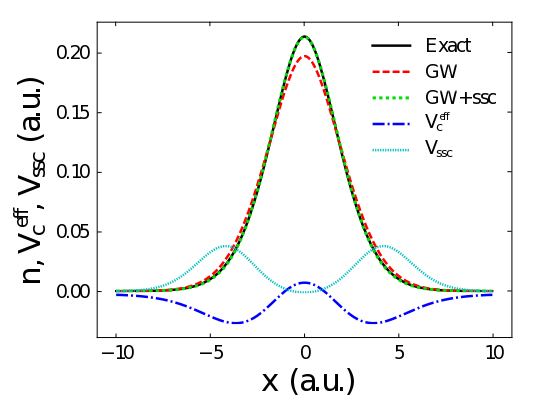
The spectral function can be obtained directly from a many-body perturbation theory calculation. However, the popular GW approximation is prone to a self-screening error
, especially in systems with strong electron localisation, which causes the approximation to yield incorrect ionisation energies. This error occurs because the electrons are screening their own removal. We have shown that this error can be corrected in a computationally efficient manner through the use of a density-functional potential (see publication). This correction allows us to obtain accurate ionisation energies in these systems.
Learn more about many-body perturbation theory and how it compares to Kohn-Sham DFT with the video below.