p  q q | from the formula ‘p implies q’ |
| p | if proposition ‘p’ is true |
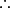 q q | conclude that ‘q’ is true |
A Prolog program consists of a file containing a set of facts and (optionally) a set of rules.
Semantically the facts constitute a declaration of a true state of affairs. As far as Prolog is concerned, any fact in its database is treated as true.
If a file containing the fact
male(phil).
|
is consulted, the goal
?-male(phil)
|
elicits the Prolog response
Yes
|
This is Prolog reporting that the expression evaluates as true with respect to its database.
With respect to the same database, the goals
?-female(phil).
?-male(chas). |
will produce the responses:
?-female(phil).
No ?-male(chas). No |
That is, with respect to this database, these facts are not known to be true.
A database consisting only of facts is not very interesting. The action picks up when rules are added.
Logic contains rules of inference. A very basic one is the one known as Modus Ponens. This takes the following
form
p  q q | from the formula ‘p implies q’ |
| p | if proposition ‘p’ is true |
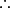 q q | conclude that ‘q’ is true |
For example:
| If John is drunk, then John is happy |
| John is drunk |
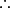 John is happy John is happy |
Prolog includes conditional formulae (like p  q, but with some syntactic reorganisation), and an algorithm for
computing inferences using Modus Ponens, but before we look at how rules are represented in Prolog, we need to look in
more detail at the relationship between standard logic and Prolog.
q, but with some syntactic reorganisation), and an algorithm for
computing inferences using Modus Ponens, but before we look at how rules are represented in Prolog, we need to look in
more detail at the relationship between standard logic and Prolog.
The kind of logic used by Prolog is a subset of First Order Logic called quantifier-free Horn Clause Logic. As the name suggests, there are no existential or universal quantifiers. Instead, any variable is implicitly assumed to be universally quantified. The statement
male(X).
|
is therefore to be taken as 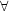 x.male(x), or ’Everything is male’.
x.male(x), or ’Everything is male’.
Note that any expression which begins with a capital letter or with the underscore character is a variable in Prolog.
The implication sign  or
or  is represented in Prolog as :-, and the order of antecedent and consequent is reversed, so
p
is represented in Prolog as :-, and the order of antecedent and consequent is reversed, so
p  q in Prolog will become q :- p.
q in Prolog will become q :- p.
Horn Clause logic is characterised by the fact that it allows only one term2 in the consequent of a conditional (i.e. before the :-). What follows the conditional must be a term (possibly complex and consisting itself of subterms including conjunctions and disjunctions).
Conjunctions, i.e. expressions which take the logical form p  q are realised in Prolog as p , q, with a comma replacing
the standard conjunction sign. So, a term p , q is true iff both p and q are true.
q are realised in Prolog as p , q, with a comma replacing
the standard conjunction sign. So, a term p , q is true iff both p and q are true.
Disjunctions, i.e. expressions which take the logical form p  q are realised in Prolog as p ; q, with a
semicolon replacing the standard disjunction sign. So, a term p ; q is true if p is true or q is true (or both
are).
q are realised in Prolog as p ; q, with a
semicolon replacing the standard disjunction sign. So, a term p ; q is true if p is true or q is true (or both
are).
The formula 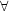 x.
x. y.female(x)
y.female(x)  parent(x,y)
parent(x,y)  mother(x,y) (‘If x is female and y’s parent, then x is y’s mother’.)
translates into Prolog as
mother(x,y) (‘If x is female and y’s parent, then x is y’s mother’.)
translates into Prolog as
mother(X, Y):-
female(X), parent(X, Y). |
The part of the rule preceding the implication sign (i.e. mother(X, Y)) is termed the head of the rule and the part to the right of the implication sign is termed the body of the rule.
David Warren, writing in The Art of Prolog (xi) writes,
The main idea was that deduction could be viewed as a form of computation, and that a declarative statement of the form:
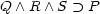
could also be interpreted procedurally, as:
“To solve P, solve Q and R and S.”
This is what Prolog does.
Given a rule such as the following:
mother(M, C):-
female(M), parent(M, C). |
it attempts to prove a goal such as:
?-mother(liz, chas).
|
by first proving female(liz) and then (if this is successful) by proving parent(liz, chas). If this process fails at any point, Prolog will report its failure with no.
Note that the deduction algorithm proceeds in a left-to-right, depth-first order.
A set of facts and rules constitutes a (logic) program.