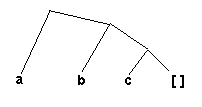
The first element of a list is called the head of the list, and the remainder is called the tail of the list. Note that (perhaps counterintuitively) the last element of every non-empty list is the empty list; although the normal Prolog notation suppresses this fact. So a is the head of all the above lists; [ ] is the tail of the first example, [b] is the tail of the second example, and [b, c] is the tail of the third example.

Because of the importance of the distinction between the head and tail of a list, Prolog provides a convenient notation that can be used to match against the head and tail of any list.

[X | Y]

Where X will match against the head, and Y against the tail. (Of course, any variable names may be used, not just X and Y.)

To illustrate these concepts, we will also introduce an operator which can be used to evaluate unification (discussed in section 1.4) directly. This operator is the equals sign =/2. The expression A = B is true in Prolog, if A is a term, and B is term, and A and B unify. The following can be typed in and evaluated:

Two constants:

?- a = a.     yes     ?- a = b.     no

A constant and a variable:

?- a = X.     X = a ?     yes

Two variables:

?- X = Y.     Y = X ?     yes

Using this operator, we can illustrate how variables unify with lists:

Lists and variables are both terms:

?- [ ] = X.     X = [ ] ?

Single-element lists unify (because they have the same ‘arity’):

?- [a] = [X].     X = a ?     yes

The following fails, because the two lists have different numbers of elements:

?- [a, b] = [X].     no

The following unify because both lists are of length 2:

?- [a, b] = [X, Y].     X = a,     Y = b ?     yes

Note carefully the difference between the above and the following using Head|Tail notation.

X matches the first element of the list [a], which is the constant a, and Y matches the tail, which is the empty list:

?- [a] = [X | Y].     X = a,     Y = [ ] ?     yes

Here again, X matches with a, and Y matches with the tail of the list [a, b], which is itself the list [b]:

?- [a, b] = [X | Y].     X = a,     Y = [b] ?     yes

Finally, a three element list:

?- [a, b, c] = [X | Y].     X = a,     Y = [b, c] ?     yes

A couple of trivial examples of predicates using lists are the following:

2.1.2 first/2

A predicate, which when supplied with a list a first argument, returns the first element of the list as its second argument:⁵

first([First|Rest], First).

2.1.3 second/2

One which returns the second element of a list:

second([First, Second|Rest], Second).

2.1.4 tail/2

One that returns the tail of a list:

tail([First|Tail], Tail).

2.1.5 Remarks on Variables

Naming variables The only syntactic requirement that Prolog places on variables is that they start either with an upper case letter, or with an underscore. This means that you could restrict yourself to writing X, Y or Z when you want a variable. For example, the program first/2 in footnote 5 might look like this:

first(X, Y):-        X = [Z|W],        Y = Z.

This will do exactly the same job as the original definition, but it is not a good idea - as programs become more complex, they become very difficult to understand if you use such simple names for variables. Even this simple example illustrates how opaque such definitions can be come.

By giving your variables mnemonic names, you help to document the function of your programs and to explain to a reader (including yourself) what information the variables are intended to convey.

The anonymous variable If you have tried putting any of the above examples into a file which you then consult into SWI Prolog, you will have discovered that it complains. For example, loading the rule for second/2 produces something like the following:

Warning: (/tmp/prolcomp22722-uu:2):           Singleton variables: [First, Rest]

This is because each of the variables First and Rest occurs only once in the definition. Because the most common use of variables in Prolog is to convey information from one part of a program to another, the occurrence of any singleton variable triggers a warning, to alert the programmer to the possibility of an error. What to do?

1. Ignore the warning. It doesn’t affect the running of the program in any way; but there may be a genuine mistake hidden in the list of singleton variables which becomes hard to spot
2. Use the underscore symbol instead of your singleton variables. This would change the definition of second/2 to this

   second([_, Second|_], Second).

   Although we have two occurrences of the underscore in this definition, Prolog treats them as unrelated (and identical in interpretation to the original definition), as ‘anonymous’.

2.1.6 Exercises:

2.1.7 Recursion

The ancestor/2 problem of exercise 1 discussed above provides a classical example of recursion. Such recursive rules always have two components,

1. the base of the recursion

   ancestor(P, C) :-      parent(P, C).

   and

2. the recursion itself

   ancestor(A, D):-      parent(A, C),      ancestor(C, D).

The base of the recursion is a non-recursive clause, which, in a computational context, tells the computation when to stop. Here the minimal definition of ancestor is a parent. The recursion crucially involves the predicate calling itself.

2.1.8 member/2⁶

A classical example of recursion in list-processing is identifying whether some item is an element of a list. This predicate is commonly called member/2. It is true if the item is on the list, and false otherwise. The base is that situation where we can be sure that we have found the item in question on the list. The limiting case here would be if the item sought is the first one on the list. We can generalise from this to the following clause:

member(Item, List):-      List = [Item|Rest].

This is OK if the item sought is indeed the first item, but what if it isn’t? In that case, we need to ignore the first item and proceed to check the remainder (i.e. the tail) of the list (note the use of the anonymous variable for the item we aren’t interested in):

member(Item, [_|Tail]):-      member(Item, Tail).

If the item sought is on the list, this procedure will find it, and Prolog will respond with ‘yes’; if not, it will fail, and Prolog will respond with ‘no’.⁷ Note that, as usual with many Prolog predicates, member/2 can be used to generate solutions; if the second argument is instantiated to a list and the first is a variable, the predicate can to used to select items off the list:

?- member(X, [a, b, c]).     X = a ? ;     X = b ? ;     X = c ? ;     no

2.1.9 append/3

Another classical example of recursion is the predicate append/3. This predicate’s three arguments are all lists. append(X, Y, Z) is true if the Z is a list that is the result of sticking the list Y onto the end of the list X. For example, append([a,b], [c,d], [a,b,c,d]) is true.

The definition of append/3 is similar to that of member/2 in that both involve working down a list item by item. In the case of append/3, however, no test is being carried out, and eventually the end of one of the lists will be reached, leaving the empty list. This gives the base: what is the result of appending an empty list to a list L? Clearly just L. In Prolog:

append([ ], List, List).

What if the first list isn’t empty? We need to take its head, save it, and stick it onto the front of the result. The result itself comes about as the consequence of carrying out the same procedures on the tail of the list. This is the recursive clause:

append([Head|Tail], List, [Head|Result]):-        append(Tail, List, Result).

append/3 can also be used to generate solutions. Here are some examples:

1. last argument a variable

   ?- append([a,b], [c,d], X).     X = [a,b,c,d] ?     yes

2. first argument a variable

   ?- append(X, [c,d], [a,b,c,d]).     X = [a,b] ?     yes

3. second argument a variable

   ?- append([a,b], X, [a,b,c,d]).     X = [c,d] ?     yes

4. first two arguments variables (and multiple solutions requested)

   ?- append(X, Y, [a,b,c,d]).     X = [ ],     Y = [a,b,c,d] ? ;     X = [a],     Y = [b,c,d] ? ;     X = [a,b],     Y = [c,d] ? ;     X = [a,b,c],     Y = [d] ? ;     X = [a,b,c,d],     Y = [ ] ? ;

2.1.10 Exercises

Hint: in all of the following, the base involves the case where the first list argument is the empty list.