Martin Bland
Professor of Medical Statistics
St. George's Hospital Medical School
This is a slightly expanded version of a talk given at the Annual Scientific Meeting: Clinical Radiology of the Royal College of Radiologists, 19 September, 2001.
Published as: Bland JM and Altman DG. (2003) Applying the Right Statistics: Analyses of Measurement Studies. Ultrasound in Obstetrics and Gynecology, 22, 85-93.
Many research papers in radiology concern measurement. This is a topic which in the past has been much neglected in the medical research methods literature. When I was first approached with a question on measurement error, I turned in vain to my books. I had to work it out myself.
I am going to deal in this talk with two types of study: the estimation of the agreement between two methods of measurement, and the estimation of the agreement between two measurements by the same method, also called repeatability. In both cases I shall be concerned with the question of interpreting the individual clinical measurement. For agreement between two different methods of measurement, I shall be asking whether we can use measurements by these two methods interchangeably, i.e. can we ignore the method by which the measurement was made. For two measurements by the same method, I shall be asking how variable can measurements on a patient be if the true value of the quantity does not change and what this measurement tells us about the patient's true or average value.
I shall avoid all mathematics, which even an audience as intelligent as this one finds difficult to follow during a presentation, except for one formula near the end, for which I shall apologise when the time comes. Instead I shall show what happens when we apply some simple statistical methods to a set of randomly generated data, and then show how this informs the interpretation of these methods when they are used to tackle measurement problems in the radiology literature.
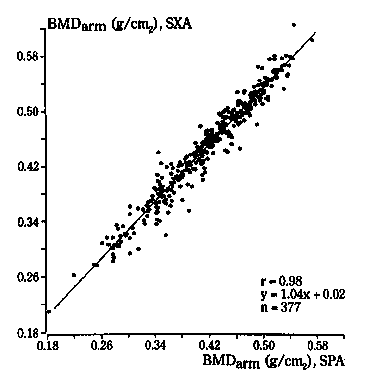
For an example of the sort of study with which I shall be concerned, Borg et al. (1995) compared single X-ray absorptiometry (SXA) with single photon absorptiometry (SPA). They produced the following scatter plot for arm bone mineral density:

The analysis uses a correlation coefficient and a regression line. In this talk I shall show why correlation might be misleading, because it is dependent on the range of measurements and the way the sample of subjects was chosen and because it ignores any systematic difference between the two methods of measurement. I shall go on to show how regression can be misleading when the intercept and slope are interpreted. I shall then show an appropriate use of regression. I shall then describe a simple alternative approach, the 95% limits of agreement. I shall show how the assumptions of this can be checked using plots of difference against average. I shall explain why plots of difference against standard method might be misleading. I shall show how measurement error and agreement can be estimated in comparable ways. I shall then show how confidence intervals for the limits are easy to calculate.
In the simplest case, we start with two observations on each of a group of subjects. These observations may be by two different methods, by the same method but different observers, or by the same method and the same observer. I shall use some randomly generated data. This is not because I do not have any real data, but because with randomly generated data we know the answer.
I generated 100 observations from a Normal distribution with mean 10 and standard deviation 3, to represent the true value of the quantity being measured. Now, we create two measurements, X and Y, by adding some measurement error to the true value.
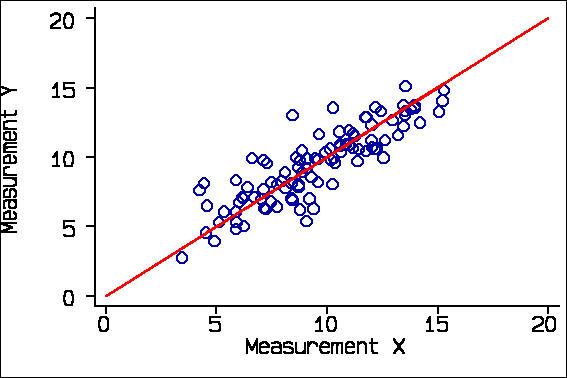
The red line is the line of equality, where X and Y are exactly the same. This is a line through the origin at 45 degrees to the axes. I shall come to the regression line later.
This is an ideal data set, as we know that X and Y both measure the same thing, that there are no systematic biases, and that errors are the same throughout the range. I shall compare the results from this ideal data set with some analyses drawn from the radiology literature and show how these can be misinterpreted. This is a very difficult area and I would not want the authors of my examples to be thought of as being foolish or perverse in their approach to the analysis. These are typical examples.
One obvious analysis is a correlation coefficient. For these data the correlation coefficient between Measurement X and Measurement Y is r = 0.86, P<0.0001.
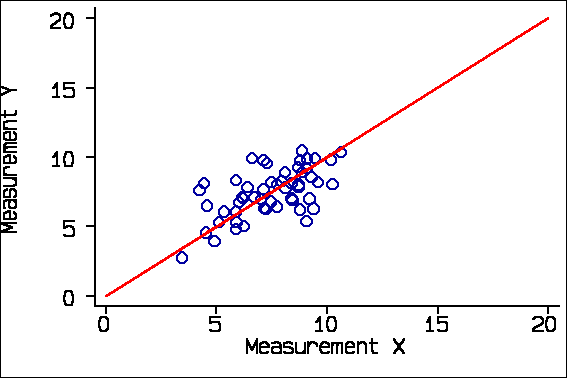
There are two problems with this. The first is that correlation depends on the range of the variables. The second is that the correlation coefficient describes association, not agreement. Correlation depends on the range of the variables. For example, if we consider only subjects whose true measurement would be 10 or less we get r = 0.60:
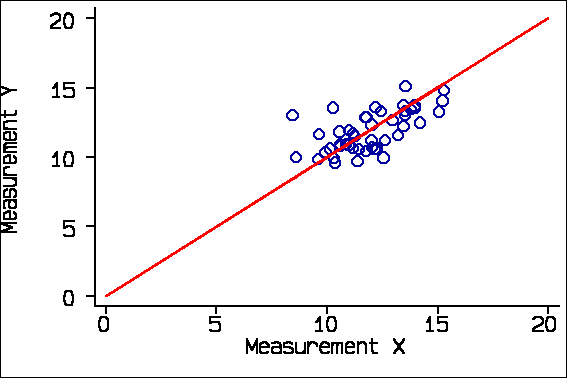
and if we consider only subjects whose true measurement would be greater than 10 we get r = 0.62:
If we take several pairs of measurements on the same subject, who is not changing as we do it, the correlation can be zero. So the correlation coefficient depends on the group of subjects selected. It should be used only if we have a representative sample of the patient population we wish to study.
Consider this example from Schild et al. (2000) comparing final fetal weight estimated by three-dimensional ultrasound with actual birth weight.
r=0.976, P<0.01, n=65,
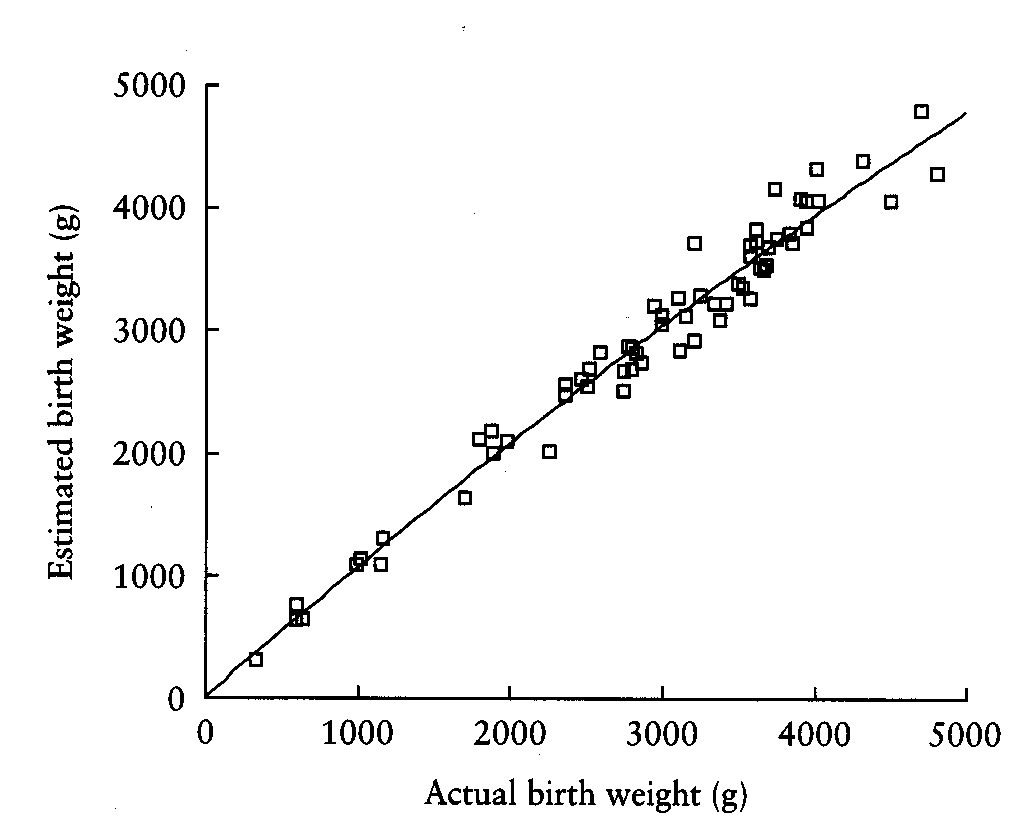
The distribution of birth weight shows that there are many more low birthweight babies than we would expect in a representative sample of births. There are 4/65 below 1000 gms. The correlation coefficient, is much larger than it would be in a representative sample.
The second problem with correlation is that it looks at the degree of association, not agreement. If I have a third measurement Z, which consistently overestimates by 2 units, the correlation of Measurement Y with Measurement Z is the same as its correlation with Measurement X, 0.86
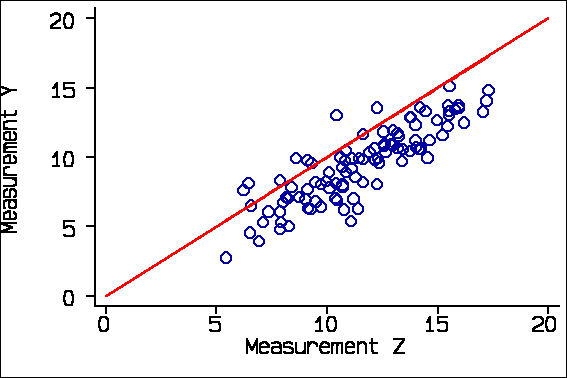
The correlation between Y and Z is the same as between Y and X, but the agreement is not.

Large systematic differences or biases are possible. For example, Bakker et al. (1999) investigated the agreement between renal volume measurements by UltraSound and Magnetic Resonance imaging. Their data for 40 kidneys were as follows:
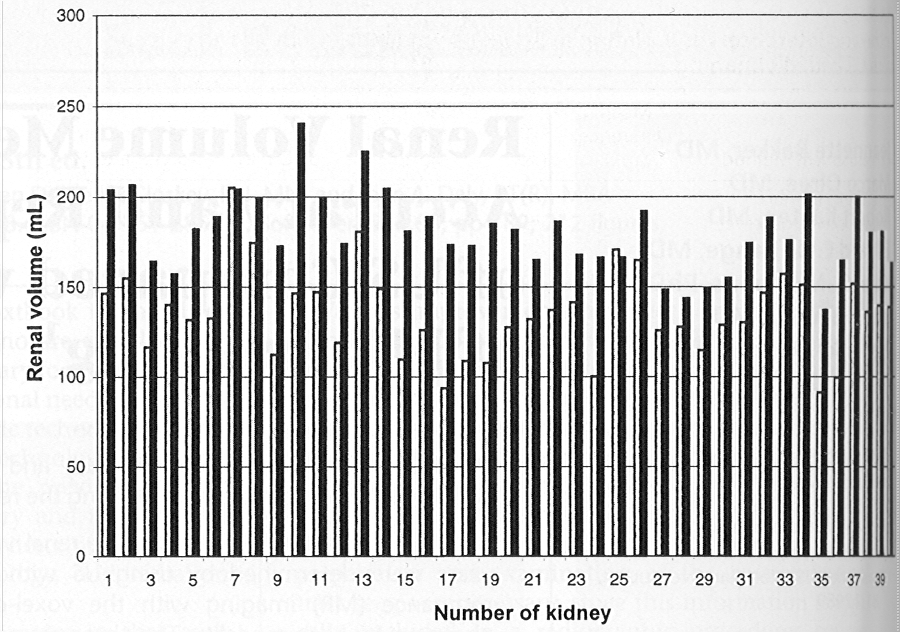
The black bars represent the MR measurements and the white bars the US.
There is a clear and significant mean difference of about 25% between the two methods. A correlation coefficient would complete miss this difference and thus be highly misleading.
Correlation is thus inappropriate for the study of agreement between different methods of measurement. Despite this, people do it.
For example, Borg et al. (1995) compared single X-ray absorptiometry (SXA) with single photon absorptiometry (SPA). They produced the following scatter plot for arm bone mineral density:

This looks like good agreement, a tight cloud of points and a high correlation of r=0.98. But should this make us think we could use bone mineral densities measured by SXA and SPA interchangeably? Look what happens when we add the line of equality to the diagram:
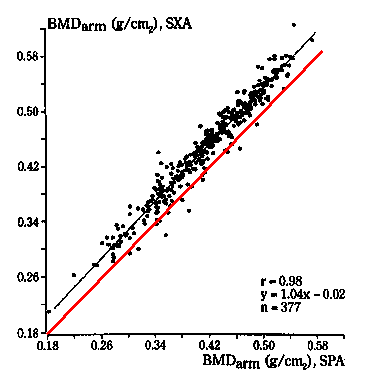
Nearly all the points lie to the left of it, and there is a clear bias. The SXA measurements tend to exceed the SPA measurements by 0.02 g/cm2.
Some applications of regression are also inappropriate. For the randomly generated data, the regression line is shown below:
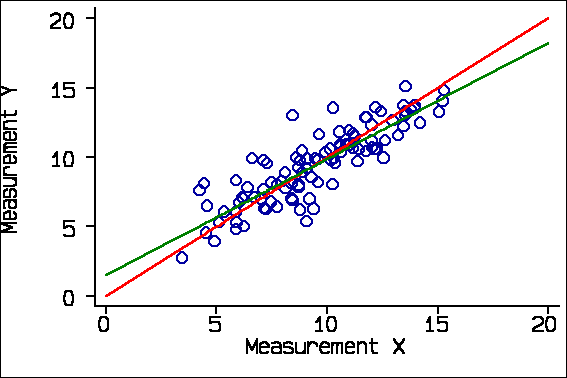
The green regression line does not coincide with the red line of equality. It does not go through the origin and its slope is less than one. If we look at the computer output, we see that the slope is 0.84, with 95% confidence interval 0.74 to 0.94, It is therefore significantly different from 1.0. Similarly, the intercept is significantly different from 0.0.
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf.
Interval]
---------+--------------------------------------------------------------------
x | .8372939 .0497111 16.843 0.000 .738644 .9359439
_cons | 1.492289 .4939103 3.021 0.003 .51214 2.472438
------------------------------------------------------------------------------
The reason for this is that regression attempts to predict the observed Y from the observed X, not the true Y from the true X. The errors in X and Y reduce the slope of the line and so raise the lower end and lower the upper end. Doing the regression the other way round, with X as dependent, has the same effect:
------------------------------------------------------------------------------
x | Coef. Std. Err. t P>|t| [95% Conf.
Interval]
---------+--------------------------------------------------------------------
y | .8876808 .0527026 16.843 0.000 .7830943 .9922674
_cons | 1.122613 .5194797 2.161 0.033 .0917224 2.153503
------------------------------------------------------------------------------
Again the slope is significantly less than one and the intercept significantly greater than zero.
Bankier et al. (1999), in a study of subjective visual grading versus objective quantification with macroscopic morphometry and thin-section CT densitometry in pulmonary emphysema, reported the following table:
Linear Regression Results: Subjective Scores and
Densitometric and Morphometric Measurements
----------------------------------------------
Subjective Score Subjective Score
and Densitometric and Morphometric
Reader Measurement Measurement
----------------------------------------------
1 0.350,1.059 0.629,1.365
2 -0.008,0.598 0.443,1.147
3 0.002,0.658 0.854,1.038
----------------------------------------------
Note. Data are 95% CIs for the intercepts of
regression lines
These measurements were not on the same scale, but all scales had a common point at zero. Bankier et al. (1999) interpret this table thus: "All but one of the CIs did not contain zero, which is suggestive of systematic overestimation of emphysema when compared with objective measurements." I disagree. This is what we would expect to see if there were no such bias.
Others have tested the null hypothesis that the slope is equal to 1.00, which we should not expect to be true if the agreement is good.
Hence we can see that although regression and correlation are used they are used inappropriately. I shall return to an appropriate application of regression later.
I mentioned earlier that there is an appropriate use of regression in the evaluation of agreement. We can regress the old measurement on the new and calculate the standard error of a prediction of the old from the new. We can use this to estimate a predicted old measurement for any observed value of the new, with a confidence interval, called a prediction interval. This gives us something akin to the limits of agreement. The problem is that it is not constant, being smallest near the middle of the range and wider as we get further towards the extremes. This is quite marked for small samples, but not for large. For the X Y data, regarding X as the old or standard method and Y as the new, we get:
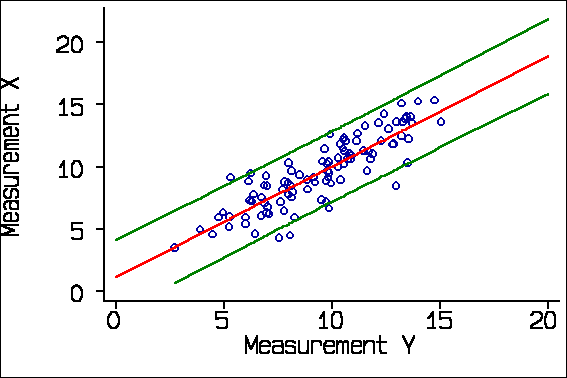
Here the spreading out is very small. If we use a smaller sample, the spreading out is clearer:
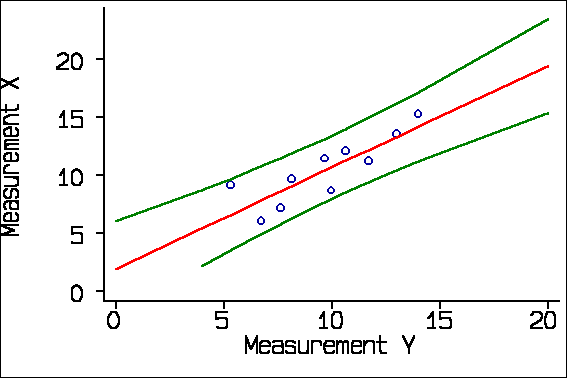
This application of regression is particularly useful when the two methods of measurement have different units, as in the study of subjective visual grading versus objective quantification with thin-section CT densitometry Bankier et al. (1999), described above. I analysed my very first methods of measurement study this way.
When Doug Altman and I wrote our first paper on comparing methods of measurement (Altman and Bland, 1983), we were mainly concerned with exposing these potentially misleading approaches. However, we thought that we should suggest a valid method of analysis too. Our proposal was the limits of agreement method. We start with the difference between measurement by the two methods, which we thought we should estimate. We calculated the mean and standard deviation of these differences. Then we calculated the mean difference plus and minus 1.96 standard deviations. 95% of differences should lie between these limits.
For the X Y data, the differences Y-X have mean -0.06 and standard deviation 1.46. Hence the 95% limits are -0.06 - 1.96*1.46 = -2.92 and -0.06 + 1.96*1.46 = 2.80. Hence a measurement by Method Y would be between 2.92 units less than a measurement by Method X and 2.80 greater.
We thought this was an Aunt Minnie, so obvious and so clearly answering the question as to need no justification (Applegate and Neuhauser 1999). We therefore did not go into detail. In a later paper (Bland and Altman 1986) we elaborated the idea and gave a worked example.
The width of the 95% limits of agreement, -2.92 to 2.80, is 5.7. For the same data, the average width of the prediction interval found by regression is also 5.7. These two approaches are similar, but the limits of agreement is much simpler and easier to express and interpret.
For a recent practical example, Cicero et al. (2001) compared cervical length at 22-24 weeks of gestation measured by transvaginal and transperineal-translabial ultrasonography. Their data looked like this:
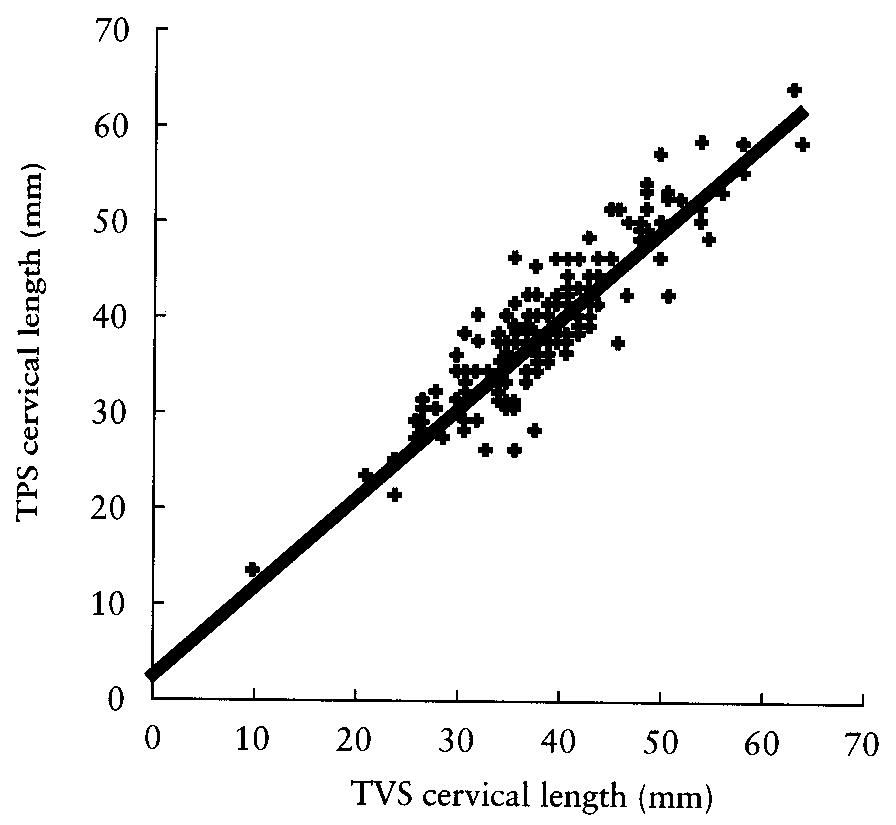
and they quoted the limits of agreement as -5.8 mm to 6.1 mm. Interestingly, they also quoted r=0.934, P<0.0001 and that line is the regression line, not the line of equality. Old habits die hard.
The 95% limits of agreement depend on some assumptions about the data: that the mean and standard deviation of the differences are constant throughout the range of measurement, and that these differences are from an approximately Normal distribution. To check these assumptions we proposed two plots: a scatter diagram of the difference against the average of the two measurements and a histogram of the differences. For the X-Y data, these look like this:
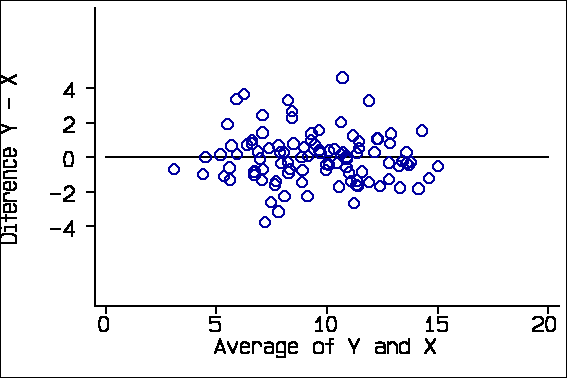
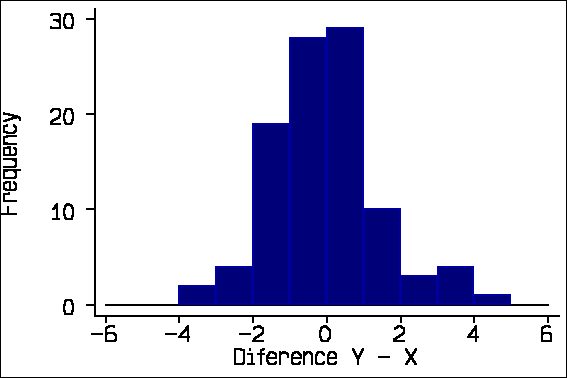
We also suggested adding the 95% limits of agreement and the mean difference to the scatter plot:
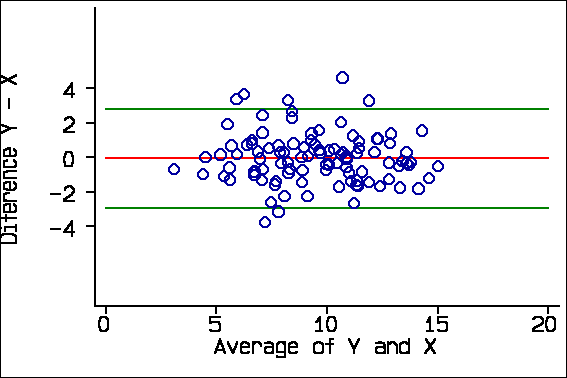
Cicero et al. (2001) show such a plot:
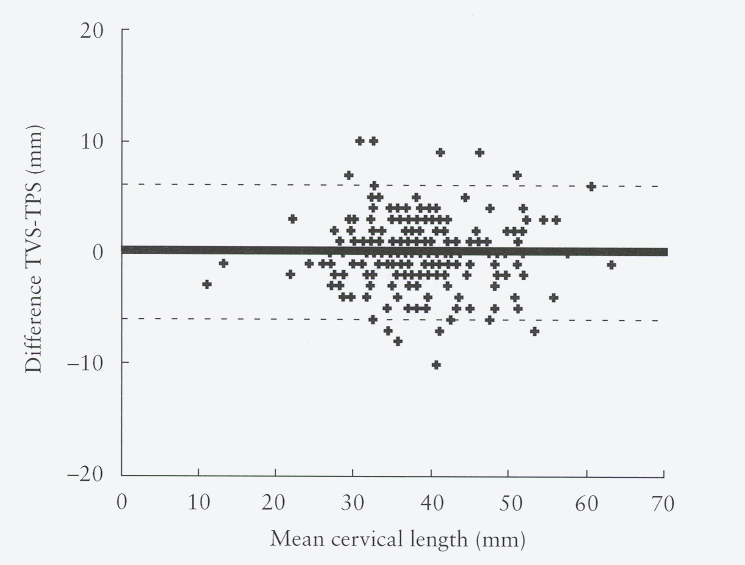
About 95% of points should lie within the limits. (In this graph there are many overlapping points.)
To our chagrin, the histogram does not seem to have been adopted with the same enthusiasm, but the scatter plot alone is a reasonable check. Also to our chagrin, many researchers seem to think that the plot is the analysis. It is not, of course, but only a check on the assumptions of the limits of agreement.
These assumptions are not always met and checking is essential. In a study of fetal lung volume measurement using three-dimensional ultrasound, Bahmaie et al. (2000) produced the following difference against mean plot for measurements by two different observers:
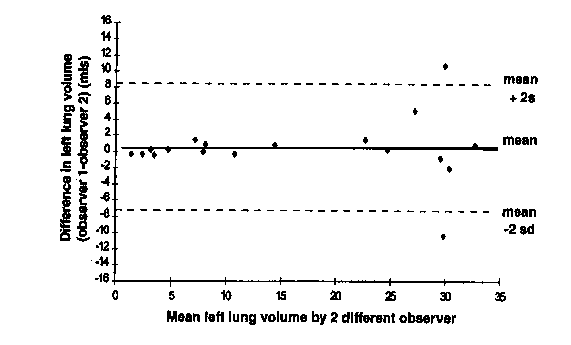
This shows a divergence as the magnitude increases, making the limits of agreement suspect.
The reason for plotting the difference against the average, rather than either of the measurements singly, is that Y-X and X are inevitably correlated. For the X-Y data these correlations are:
Correlation with difference Y-X Average of X & Y -0.06, P=0.6 X -0.31, P=0.002 Y +0.21, P=0.04
We expect Y-X and X to be negatively correlated and Y-X and Y to be positively correlated when the difference is not really related to the magnitude, as we know to be the case in this example. Y-X and the average of Y and X will not be correlated if there is no real relationship. We can see this in the plots of difference against X and against Y:
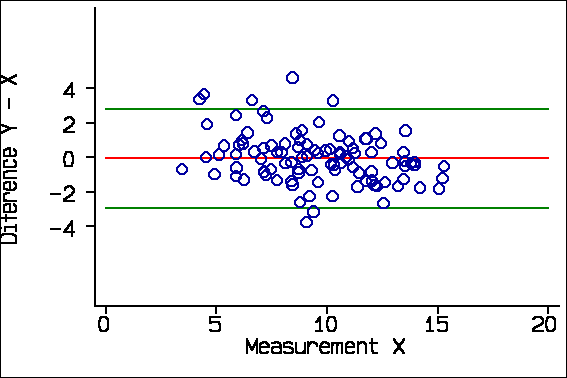
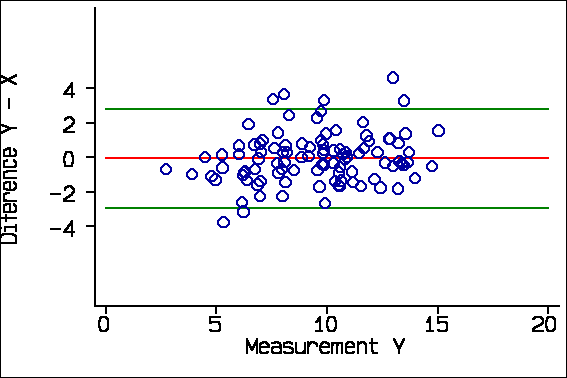
Now, consider this example from Schild et al. (2000) comparing final fetal weight estimated by three-dimensional ultrasound with actual birth weight. There is no evidence of any tendency for the points to divert from the line of equality in the scatter diagram:

They plotted the percentage error (essentially the difference) against the actual birthweight:
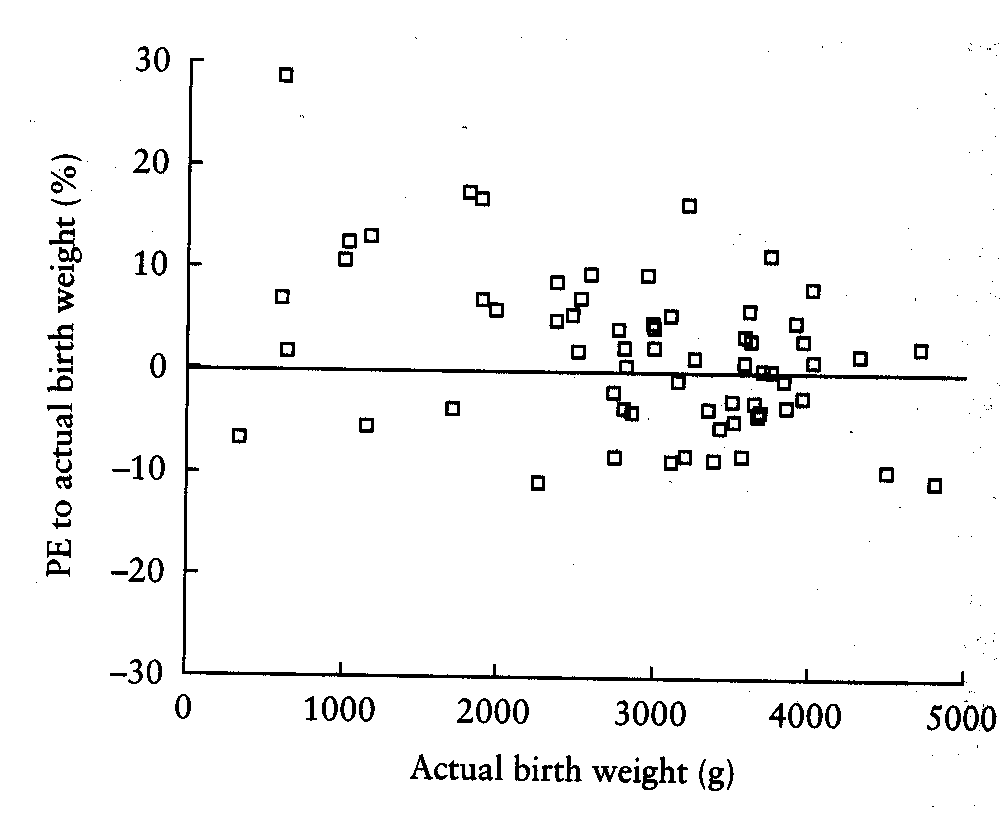
The downward trend in the graph is readily apparent. This can be seriously misleading. Consider the following from a comparison of MR with conventional arthrography (Jaramillo et al, 1999):
"For all parameters, the difference between the measurements of the two modalities depended on the magnitude of the measurements. By using arthrography as the standard, a slope test indicated overestimation with MR imaging at small measurements and an underestimation at large measurements (all P<0.001)."
If they regressed MR minus arthrography on arthrography, this is what we would expect in the absence of a true relationship between difference and magnitude (Bland and Altman 1995). It would look like this:
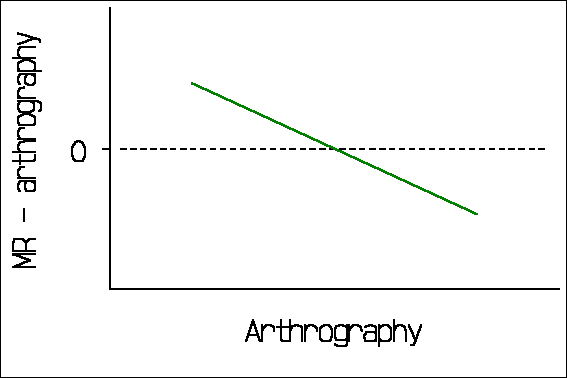
The 95% limits of agreement method has been widely cited and quite widely used, though many citers do not appear to have read the paper. For example, Jaramillo et al. (1999), cited above, say in their methods section that "For each parameter, agreement between MR imaging and arthrography was investigated using the method of Bland and Altman [1986]. Arthrography was considered to be the standard and differences between methods were calculated and plotted. A slope test was used to assess whether these differences varied systematically over the range of measurements." The results section of the paper contains no limits of agreement, but rather correlation and rank correlation coefficients with P values! As for plotting difference against a standard measurement, Bland and Altman (1986) actually wrote "It would be a mistake to plot the difference against either value separately because the difference will be related to each, a well-known statistical artefact. [Gill et al. 1985)]".
Measurement error can be analysed in a manner analogous to the limits of agreement. The main difference is that there should not be any bias, which simplifies things. Correlation can be used provided there is a population from which the sample can be regarded as a representative sample, in which case it is a measure of the information content of the measurement. However, this does not help us to interpret a clinical measurement on a given patient. To do this we need to consider the variability between repeated measurements on the same subject. If we calculate the standard deviation of the differences between pairs of repeated measurements, we can calculate 1.96 times this standard deviation. This gives the repeatability coefficient, which is the difference which will be exceeded by only 5% of pairs of measurements on the same subject (British Standards Institution 1975). It is thus directly comparable to the 95% limits of agreement. Thus we can use this to compare agreement which a new method of measurement would have with a standard method, with the agreement which the new method would have with itself.
In our 1986 paper we advocated a design where each method would be used twice on each subject, so that limits of agreement between the two method and coefficients of repeatability for each method separately could be compared. We regret that this has not been widely adopted by researchers.
Another feature which we stressed in the 1986 paper was that agreement is a
question of estimation, not hypothesis testing. Estimates are usually made
with some sampling error, and limits of agreement are no exception. We showed
how to estimate confidence intervals for the limits of agreement. (The
Lancet editorial team, in the person of David Sharp, cut the length of
the paper, and much improved it in the process. However, when I explained the
importance of the deleted paragraph on confidence intervals, it was
reinstated.) Another regret is that these confidence intervals are seldom
quoted. For the data of Cicero et al. (2001), the mean difference was
0.2 mm with standard deviation 3.0 mm, giving 95% limits of agreements -5.8 mm
to +6.1 mm. There were 234 cases. The standard error of the limits is
approximately ![]() (for which bit of
algebra I apologise!). This give
(for which bit of
algebra I apologise!). This give ![]() .
The 95% confidence interval for the limits of agreement is given by plus or
minus 1.96 standard errors = 0.67, so for the lower limit the confidence
interval is -6.5 to -5.1 and for the upper limit the 95% confidence interval is
+5.4 to +6.8. Not so hard, really!
.
The 95% confidence interval for the limits of agreement is given by plus or
minus 1.96 standard errors = 0.67, so for the lower limit the confidence
interval is -6.5 to -5.1 and for the upper limit the 95% confidence interval is
+5.4 to +6.8. Not so hard, really!
The limits of agreement approach is fundamentally very simple and direct. Provided its assumptions of uniform mean and standard deviation are met, it can be carried out by anyone with basic statistical knowledge. It provides statistics which are easy to interpret in a meaningful way.
It can be extended to many more complex situations (Bland and Altman 1999):
Altman DG, Bland JM. (1983). Measurement in medicine: the analysis of method comparison studies. The Statistician 32: 307-317.
Applegate, KE, Neuhauser, DVB. (1999) Whose Aunt Minnie? Radiology 211: 292.
Bahmaie, A, Hughes, SW, Clark, T, Milner, A, Saunders, J, Tilling, K, Maxwell, DJ. (2000) Serial fetal lung volume measurement using three-dimensional ultrasound. Ultrasound in Obstetrics & Gynecology 16: 154-158.
Bakker, J, Olree, M, Kaatee, R, de Lange, EE, Moons, KGM, Beutler, JJ, Beek, FJA. (1999) Renal volume measurements: Accuracy and repeatability of US compared with that of MR imaging. Radiology 211: 623-628.
Bankier, AA, De Maertelaer, V, Keyzer, C, Gevenois, PA. (1999) Pulmonary emphysema: Subjective visual grading versus objective quantification with macroscopic morphometry and thin-section CT densitometry. Radiology 211: 851-858.
Bland JM, Altman DG. (1986). Statistical methods for assessing agreement between two methods of clinical measurement. Lancet i: 307-310.
Bland JM, Altman DG. (1995) Comparing methods of measurement: why plotting difference against standard method is misleading. Lancet 346, 1085-7.
Bland JM, Altman DG. (1999) Measuring agreement in method comparison studies. Statistical Methods in Medical Research 8: 135-160.
Borg, J, Møllgaard, A, Riis, BJ. (1995) Single x-ray absorptiometry: performance characteristics and comparison with single photon absorptiometry Osteoporosis International 5: 377-381.
British Standards Institution. (1975) Precision of test methods 1: Guide for the determination and reproducibility for a standard test method (BS 597, Part 1). London: BSI.
Cicero, S, Skentou, C, Souka, A, To, MS, Nicolaides, KH. (2001) Cervical length at 22-24 weeks of gestation: comparison of transvaginal and transperineal-translabial ultrasonography. Ultrasound in Obstetrics & Gynecology 17: 335-340.
Gill JS, Zezulka AV, Beevers DG, Davies P. (1985) Relationship between initial blood pressure and its fall with treatment. Lancet i: 567-69.
Jaramillo, D, Galen, T, Winalski, CS, DiCanzio, J, Zurakowski, D, Mulkern, RV, McDougall, PA, Villegas-Medina, OL, Jolesz, FA, Kasser, JR. (1999) Legg-Calvé-Perthes disease: MR imaging evaluation during manual positioning of the hip--Comparison with conventional arthrography. Radiology 212: 519-525.
Schild, RL, Fimmers, R, Hansmann, M. (2000) Fetal weight estimation by three-dimensional ultrasound. Ultrasound in Obstetrics & Gynecology 16: 445-452.
Back to Martin Bland's Home Page.
This page is maintained by Martin Bland.
Last updated: 12 January, 2005.