Go back to Table of Contents
Go back to Section 3.8
Continue to Section 4.5
4.0 Examples of Application of the Transactional Interpretation
The previous discussion contrasting the interpretations of quantum mechanics has been fairly abstract. Now we conclude with a more concrete elucidation of the TI, demonstrating the power of its imagery by presenting examples of its application. The TI is a conceptual model which provides a way of clearly visualizing complicated quantum processes. It is a way of thinking rather than a way of calculating. It may have considerable pedagogical potential as a more intuitive way of teaching quantum mechanics. It can provide insight and intuition which have been unavailable up to now in considering quantum phenomena. Here we will use the TI to examine and illuminate some of the "paradoxes", gedanken experiments, and real experiments which have been collected in the quantum mechanics museum of curiosities.
We have elected to describe most of these gedanken experiments using photons of visible light passing through polarizing filters or beam splitters before detection by quantum-sensitive photomultiplier tubes. We have used circular and linear polarization of light as archetypes of non-commuting observables. Other authors (e.g., Feynman, 1965) prefer to describe the equivalent experiments using electrons instead of photons, electron spin orientation instead of photon polarization, Stern-Gerlach apparatus instead of polarizing filters and splitters, and electron counters instead of photomultipliers. While there may be differences in detail in such descriptions, there should be no fundamental change in the quantum effects illustrated. We feel that on balance the polarized photon description is better connected to direct experience and that once embarked on a particular mode of description it is desirable to use consistent apparatus. However, the reader is assured that these gedanken experiments can be "performed" with electrons, protons, or even neutrinos with only minor descriptional differences. Analogous experiments could, in most cases, have been constructed using as non-commuting observables electron spin states along the x-axis and the y-axis or even position and momentum observables. In most cases a real experiment could most easily be actually performed using photons of visible light and polarization observables.
4.1 Renninger's Negative-Result Gedanken Experiment
This is a gedanken experiment focusing on the collapse of the SV produced by the absence of an interaction of the system measured (a photon) with measurement apparatus. It was suggested by Renninger (1953) and was featured by de Broglie (1964) in his book on the interpretation of quantum mechanics. Dicke (1981) has recently stimulated renewed interest in this kind of "interaction-free measurement". The experimental arrangement is shown in ![]() Fig. 6.
Fig. 6.
Source S is located at the center of a spherical shell E2 of radius R2. The interior of E2 is lined with a scintillating material which will produce a detectable flash of light which will be seen by the observer if E2 is struck by a charged particle, e.g., an alpha particle. Inside E2 is a partial concentric sphere E1 of radius R1, also lined with scintillator viewed by the observer. Partial sphere E1 subtends solid angle 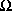 1 as viewed from the position of source S. The portion of E2 which is not shadowed by E1 therefore subtends a solid angle
1 as viewed from the position of source S. The portion of E2 which is not shadowed by E1 therefore subtends a solid angle 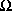 2=4
2=4 -
-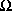 1. The source S is arranged so that on command it will emit exactly one alpha particle with an angular dependence which is completely isotropic, and with a velocity which is equal to V.
1. The source S is arranged so that on command it will emit exactly one alpha particle with an angular dependence which is completely isotropic, and with a velocity which is equal to V.
Now let us consider the state vector |S(t)> as a function of time t, where t is the time which has elapsed since the source S has been commanded to emit an alpha particle. Before the alpha particle has traversed the distance R, i.e., for 0<t<(R1/V), the probability that the particle will produce a scintillation at E1 is P1=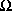 1/4
1/4 , and the probability that it will produce a scintillation at E2 is P2=
, and the probability that it will produce a scintillation at E2 is P2=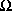 2/4
2/4 . Thus the state vector might be written as:
. Thus the state vector might be written as:
IS(t)> = p1|E1> + p2|E2> where |<p1>|2 = P1 and |<p2>|2 = P2. [14]
But now let us suppose that time t becomes greater than R1/V and that the observer does not observe a scintillation from E1. Then the state vector must collapse, with the result that the probabilities become P1=0 and P2=1 and the state vector becomes |S(t)>=|E2> for t>(R1/V). The interpretational problem as stated by Renninger and de Broglie is that the state vector has collapsed abruptly and non-linearly, and yet "the observer sees nothing at all on screen E, where nothing has happened". Thus, the absence of an interaction with the measurement apparatus leading to the absence of an observation can collapse the SV as readily as a positive and definite observation.
This gedanken experiment helps us to understand why von Neumann (1932) and Wigner (1962) stressed the need for a conscious and intelligent observer as the triggering agent for the collapse of the SV. The change in "knowledge" when no scintillation is observed at E1 when t=R1/V requires a deduction on the part of the observer as to what should have happened if the alpha particle had been aimed at E1. It correspondingly casts some doubt on Schrödinger's (1935) principle of state distinction and on Heisenberg's (1960) irreversibility criterion, since no state-distinguishing record is made at t=R1/V and no irreversible process is initiated. Furthermore, one could imagine a more elaborate version of this experiment with a very large number of partial spheres inside E2, so complicated that no human observer could possibly keep track of all the times and expectations of flashes which would signal the occurrence or elimination of various possible outcomes. And one could speculate on how the SV collapse might occur in that situation.
The TI avoids the conceptual problems implicit in this experiment by eliminating any SV collapse which occurs at some definite instant such as t=R1/V. Instead it employs an atemporal four-space description implicit in the transaction model: the state vector is emitted from the source at t=0 as a retarded OW which grows as a spherical wave front, part of which encounters E2 at t=R2/V and the remainder encounters E1 at t=R1/V. The boundary condition of S that only a single alpha particle is emitted permits one and only one transaction to occur between S and E1 or E2. The transaction will occur with a probability proportional to the CW echoes which S receives from the two possible absorbers. These echoes will be proportional to the solid angles subtended by the two possible absorbers, i.e., 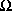 1 and
1 and 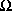 2 as expected. A single transaction forms in accordance with these probabilities through the exchange of advanced and retarded waves characterizing the transition of an alpha particle from S to E.
2 as expected. A single transaction forms in accordance with these probabilities through the exchange of advanced and retarded waves characterizing the transition of an alpha particle from S to E.
4.2 Wheeler's Delayed-Choice Experiment
The previous gedanken experiment illustrated how the absence of an observation could collapse the SV. Now we consider a gedanken experiment in which the SV must avoid collapsing after interacting with the apparatus while the experimenter decides what experiment he wishes to perform. It is an example of the "delayed choice" experiments proposed by Wheeler (1978). It is shown schematically in ![]() Fig. 7.
Fig. 7.
Here we have the usual Young's two slit interference apparatus, illuminated by an ideal source S which is a distance L from the slits. The source S emits one and only one photon in the general direction of the slits, on command from the observer who is operating the apparatus. Downstream of the slits are two different measuring devices. One of these devices is E, a photographic emulsion which, when placed in the path of the photon, will record photons at the position where they strike the emulsion. After many such events are recorded they will form an two-slit interference pattern characteristic of the photon's wavelength 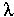 and momentum h/
and momentum h/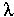 . The other measuring device consists of T1 and T2, a pair of tightly collimated telescopes with single-quantum sensitive photomultiplier tubes at their image foci, each of which is focused on one of the two slits. A photon registered by T1 or T2 means that the photon has passed through slit 1 or 2, respectively. Therefore, T1 and T2 constitute a determination of photon position.
. The other measuring device consists of T1 and T2, a pair of tightly collimated telescopes with single-quantum sensitive photomultiplier tubes at their image foci, each of which is focused on one of the two slits. A photon registered by T1 or T2 means that the photon has passed through slit 1 or 2, respectively. Therefore, T1 and T2 constitute a determination of photon position.
Such an apparatus is often used to illustrate the wave-particle duality of light. The light waves which form the interference pattern on the emulsion must have passed through both slits of the apparatus in order to interfere at the emulsion, while the photon particles which strike the photomultiplier surfaces can have passed only through the one slit at which the telescope was aimed. The emulsion measures momentum and the telescopes measure position, i.e. conjugate variables. Thus the two experimental measurements are "complimentary" in Bohr's sense. The uncertainty principle is not violated, however, because only one of the two experiments can be performed on a given photon. But Wheeler is not done yet.
The emulsion E is mounted on a fast acting pivot mechanism so that it can on command either be raised into position to intercept the photon from S or alternatively dropped out of the way so that the photon can proceed to T1 or T2. Thus when E is up we make an interference measurement requiring the photon to pass through both slits. When E is down we make a position measurement requiring that the photon pass through only one slit.
Wheeler's innovative modification of this old gedanken experiment is this: The time t>L/c at which the photon has safely passed the slits but not yet reached the apparatus is known to the experimenter, and he refrains from deciding which experiment to do, i.e., whether to place E up or down, until time T when the photon must have already passed through the slit or slits. Therefore, the photon has already emerged from the slit system when the experimenter decides whether it should be caused to pass through one slit (E down) or both slits (E up). In a sense then, the cause (emulsion down or up) has come after the effect (passage through one or two slits).
This gedanken experiment demonstrates that the physical interaction of the photon with the slit system has not collapsed the SV, which must remain uncollapsed at least until the experimenter decides which experiment to do. And since the experimenter, after having made the decision, knows whether the photon will pass through one or both slits, it can be argued from CI4 that it is his mental process of deciding which has precipitated the collapse of the SV rather than its subsequent interaction with E, T1, or T2, since after that decision is made he has the unambiguous knowledge of how many slits the photon has passed through.
Wheeler has explored the physical and philosophical implications of this and similar experiments, and has been led to assert the often quoted paradigm: "No phenomenon is a phenomenon until it is an observed phenomenon". In this statement he is emphasizing the role of the observer in precipitating an underlying indefinite reality into a definite observed state by the act of deciding on a measurement and then performing it. Again it would seem that observers, and indeed intelligent and decisive observers, are required to interpret this class of gedanken experiments using reasonable variants of the Copenhagen interpretation.
The TI, however, is able to give an account of the delayed choice experiment without resort to such observers as collapse triggers. In the TI description the source S emits the retarded OW which propagates through both slits and reaches the locus of E, where either (a) it finds the emulsion E is up and is absorbed by it as illustrated in ![]() Fig. 8a; (b) it finds E down and proceeds to T1 where it is absorbed, as illustrated in Fig. 8b; or (c) it finds E down and proceeds to T2 where it is absorbed, as illustrated in Fig. 8c. For case (a) in which the photon is absorbed by E, the advanced CW retraces the path of the OW, travelling in the negative time direction through both slits and back to source S. Therefore the final transaction, as shown in Fig. 8a, forms along paths which pass through both slits in connecting the source S with the emulsion E. The transaction is therefore a "two-slit" quantum event. The photon can be said to have passed through both slits to reach the emulsion.
Fig. 8a; (b) it finds E down and proceeds to T1 where it is absorbed, as illustrated in Fig. 8b; or (c) it finds E down and proceeds to T2 where it is absorbed, as illustrated in Fig. 8c. For case (a) in which the photon is absorbed by E, the advanced CW retraces the path of the OW, travelling in the negative time direction through both slits and back to source S. Therefore the final transaction, as shown in Fig. 8a, forms along paths which pass through both slits in connecting the source S with the emulsion E. The transaction is therefore a "two-slit" quantum event. The photon can be said to have passed through both slits to reach the emulsion.
For cases (b) and (c) the OW also passes through both slits on its way to the photomultiplier telescopes T1 and T2. However, when the absorption takes place at one of the telescopes (not both because of the single quantum boundary condition), the collimation system of that telescope prevents the CW from passing through more than one of the slits, since the collimation only permits passage through the slit at which the telescope is aimed. Thus the CW passes through only one slit in passing from T1 (or T2) to S, and the transaction which forms is characteristic of a "one-slit" quantum event. The photon can be said to have passed through only one slit to reach the telescope.
Since in the TI description the transaction forms atemporally, the issue of when the observer decides which experiment to perform is no longer significant. The observer determined the experimental configuration and boundary conditions and the transaction formed accordingly. Further, the fact that the detection event involves a measurement (as opposed to any other interaction) is no longer significant and so the observer has no special role in the process. To paraphrase Wheeler's paradigm, we might say: "No offer is a transaction until it is a confirmed transaction".
4.3. Schrödinger's Cat and Wigner's Friend
Perhaps the most famous gedanken experiment demonstrating an interpretational "paradox" of quantum mechanics is the Schrödinger's Cat Paradox (1935) illustrated in ![]() Fig. 9. Schrödinger describes a "hoellenmaschine" which dramatizes the interpretational problem. An ideally isolated system (a sealed, soundproof, and well insulated box with an adequate oxygen supply) is prepared so that it contains a Geiger counter placed near a radioactive source which emits gamma rays. The source of gamma rays is adjusted in strength so that in a period of one hour it has a probability of exactly 50% of causing the Geiger counter to record one count. The counter mechanism is connected to a solenoid device which, if a count occurs, will shatter a flask of prussic acid, thereby filling the box with lethal fumes. Of course there is also a probability of 50% that no count will occur and the flask will remain intact.
Fig. 9. Schrödinger describes a "hoellenmaschine" which dramatizes the interpretational problem. An ideally isolated system (a sealed, soundproof, and well insulated box with an adequate oxygen supply) is prepared so that it contains a Geiger counter placed near a radioactive source which emits gamma rays. The source of gamma rays is adjusted in strength so that in a period of one hour it has a probability of exactly 50% of causing the Geiger counter to record one count. The counter mechanism is connected to a solenoid device which, if a count occurs, will shatter a flask of prussic acid, thereby filling the box with lethal fumes. Of course there is also a probability of 50% that no count will occur and the flask will remain intact.
The experimenter places a cat inside the box, seals it, and leaves the system undisturbed for one hour. At the end of the hour the experimenter deactivates the counter, opens the box, and observes the state of the system. Two states are possible: a state |AC> (alive cat) in which the flask is unbroken and the cat remains alive and a state |DC> (dead cat) in which the flask has shattered and the cat has been killed . Schrödinger's question is: What is the quantum mechanical state vector of the system immediately before box is opened and the observation is made?
Quantum mechanics, as interpreted by the CI, would seem to tell us that the SV was [  |AC> +
|AC> +
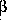 |DC> ], where
|DC> ], where 
 * =
* = 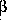
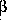 * = ½. In other words the SV of the system consists of equal components of the live cat wave function |AC> and the dead cat wave function |DC> until such time as the observer collapses the SV into one or the other of these states by making an observation, since it is the change in the observer's knowledge which precipitates the SV collapse. In the period just before the observation is made the SV describes the cat as 50% alive and 50% dead. This description, which may seem plausible enough when applied to a microscopic system (or even to a statistically large ensemble of Schrödinger's cat experiments), appears rather absurd when applied to an individual complex organism like a cat.
* = ½. In other words the SV of the system consists of equal components of the live cat wave function |AC> and the dead cat wave function |DC> until such time as the observer collapses the SV into one or the other of these states by making an observation, since it is the change in the observer's knowledge which precipitates the SV collapse. In the period just before the observation is made the SV describes the cat as 50% alive and 50% dead. This description, which may seem plausible enough when applied to a microscopic system (or even to a statistically large ensemble of Schrödinger's cat experiments), appears rather absurd when applied to an individual complex organism like a cat.
Wigner (1962) further heightened the weirdness implicit in the CI description by replacing the cat with a "friend", i.e., an intelligent observer and at the same time replacing the prussic acid mechanism with a less lethal piece of apparatus, e.g., a light bulb which is switched on when a count is recorded. The experimenter then performs the experiment, which can be considered as two experiments: (a) treating friend+box as a system, the experimenter makes an observation, and (b) treating the counter mechanism as a system, the friend makes an observation which is subsequently reported to the experimenter.
We will not reproduce Wigner's detailed analysis of this gedanken experiment here, but will state his conclusion: consciousness must have a special role in the collapse of the SV, for otherwise one must deal (a least on the philosophical level) with uncollapsed SV's containing conscious observers in a multiplicity of alternative states. Several others have suggested alternative ways of avoiding uncollapsed SV's describing conscious observers. Heisenberg (1960) has suggested that the SV collapses when the system enters the domain of thermodynamic irreversibility, e.g., as soon as a piece of macroscopic apparatus becomes involved. Schrödinger (1945) suggested that as soon as a permanent record of the system state is made, e.g., by smashing the flask, the SV is collapsed. Everett (1957) has dispatched the interpretational problem posed by these gedanken experiments by suggesting that the SV never collapses. Instead in the Everett-Wheeler interpretation of QM (see Appendix A.4) the universe "splits" with each quantum event into alternate universes, each characterized by one of the possible outcomes of the event. None of these modifications of the basic CI has gained wide acceptance, and, as discussed in Section 2 and in the Appendix, none is without its own interpretational problems.
The central focus of the problems posed by Schrödinger's Cat and Wigner's Friend is the question of when the SV actually collapses. The TI avoids the implicit dilemma because in the TI the SV collapse, i.e., the formation of the transaction, is atemporal. During the entire one hour period that the box is closed the radioactive source S of Schrödinger's apparatus sends out a very weak OW. This OW may or may not, with equal 50% probabilities, be confirmed by a CW from the Geiger counter so that a completed transaction is formed. If a transaction is formed, then the count is recorded, the flask shattered, the cat killed. If such a transaction is not formed then the cat remains alive. The SV (or OW) does indeed have implicit in it both live cat and dead cat possibilities, but the completed transaction allows only one of these possibilities to become real. Because the collapse does not have to await the arrival of the observer there is never a time when "the cat is 50% alive and 50% dead". And the need for consciousness, permanent records, thermodynamics, or alternate universes never arises. The "buck stops" at the absorber, in this case the Geiger counter, and the uncollapsed SV need not be tracked any further.
To put this another way, Schrödinger's question is: When can a quantum event be considered finished? Is it when the gamma ray leaves the radioactive nucleus? Is it when it interacts with the Geiger counter? When the flask is smashed? When the cat dies? When the observer looks in the box? When he tells a colleague what he observed? When he publishes his observations in the Physical Review? When ... ? A billiard shot is over when the billiard balls stop colliding and come to rest. But the atomic "billiard balls" of a quantum billiard shot continue to collide forever, never coming to rest so that the shot can be considered finished.
The source of confusion here is that the wrong question is being asked. The CI has lead us to ask when the SV collapses instead of how it collapses. But there is not a "when", not a point in time at which the quantum event is finished. The event is finished when the transaction forms, which happens along a set of world lines which include all of the event listed above, treating none of them as the special conclusion of the event. If there is one particular link in this event chain which is special, it is not the one which ends the chain. It is the link at the beginning of the chain when the emitter, having received various CW's from its OW, reinforces one of them in such a way that it brings that particular CW into reality as a completed transaction. The atemporal transaction does not have a "when" at the end.
4.4. Transmission of Photons through Non-Commuting Polarizing Filters
The behavior of quantum systems in response to measurements of non-commuting variables is often cited as one of the interpretational problems of quantum mechanics and has been used as a justification for the development of quantum logics. However, one can usually find excellent classical analogs of such measurements, e.g., the Fourier time-frequency complementarity of electrical pulse waveforms and the transmission of light through successive polarizing filters.
Therefore, it is instructive to consider the QM treatment of the transmission of light through polarizing filters as an illustration of the application of the TI. We will specifically select a case where the handling of complex amplitudes is required so that this aspect of the TI can be shown. ![]() Fig. 10a shows the system to be considered: A single photon of light is emitted by source S and travels along an optical bench to the single-quantum sensitive photomultiplier detector D. In traversing this path it passes through three polarizing filters which we will call H, R, and V, to indicate that, respectively, they transmit with 100% efficiency light which is in a pure state of horizontal linear polarization, right circular polarization, and vertical linear polarization, respectively, while completely absorbing light which has the orthogonal polarization.
Fig. 10a shows the system to be considered: A single photon of light is emitted by source S and travels along an optical bench to the single-quantum sensitive photomultiplier detector D. In traversing this path it passes through three polarizing filters which we will call H, R, and V, to indicate that, respectively, they transmit with 100% efficiency light which is in a pure state of horizontal linear polarization, right circular polarization, and vertical linear polarization, respectively, while completely absorbing light which has the orthogonal polarization.
This example is chosen because the operators characterizing linear polarization eigenstates do not commute with the operators characterizing circular polarization eigenstates, and so linear and circular polarization are non-commuting variables. The two descriptions (linear vs. circular) represent two related bases. In particular, if |H>, |V>, |R>, and |L> represent pure states, respectively, of horizontal linear, vertical linear, right circular, and left circular polarization, then they are related by the transformation equations:
|R> =  ( |H> + i|V>); |L> = -
( |H> + i|V>); |L> = - ( |H> - i|V>) [15a,b]
( |H> - i|V>) [15a,b]
|H> =  ( |R> + IL>); |V> = -i
( |R> + IL>); |V> = -i ( |R> - |L>) [15c,d]
( |R> - |L>) [15c,d]
where  = (2)-½ and i = (-1)½.
= (2)-½ and i = (-1)½.
The TI provides the following description of the transmission of a photon from S to D: The source S produces a retarded OW in the form of a general SV including all possible states of polarization. This wave then passes through filter H. The filter transmits {footnote 19} only |H>, i.e., that component of the SV which corresponds to a state of pure horizontal linear polarization (HLP). This wave then travels to filter R, which transmits only that component of |H> which is in a pure state of right circular polarization (RCP). From equation (15c) this is  |R>. This RCP wave then travels to filter V, which transmits only that component which is in a pure state of vertical linear polarization (VLP). From equation (15a), this will be
|R>. This RCP wave then travels to filter V, which transmits only that component which is in a pure state of vertical linear polarization (VLP). From equation (15a), this will be  (i
(i |V>)=(i/2)|V>. This VLP wave then strikes the photocathode of D and is absorbed and detected.
|V>)=(i/2)|V>. This VLP wave then strikes the photocathode of D and is absorbed and detected.
But according to the transaction model this is only half of the story. In absorbing the incident retarded wave, the photocathode must produce a "time-mirrored" advanced wave or CW. This wave will be the complex conjugate of the incident OW and has the form:
CW = OW* = [(i/2)|V>]* = (-i/2)<V| [16]
The advanced CW travels back along the track of the incident OW until it encounters filter V, where it is perfectly transmitted since it is already in a state of pure VLP.
The CW then proceeds along the track of the OW until it reaches filter R, where only its RCP component is transmitted. We can use equations (15) for changing the basis of advanced waves by taking the complex conjugates (i.e., the time reverse) of both sides of the equations to obtain a new set of transformation equations which we will denote as (15)*. Employing that procedure, equation (15d)* shows us that the transmitted CW will have the form:
(-i/2) [i  <R|] = ½
<R|] = ½  <R| [17]
<R| [17]
The CW then proceeds until it reaches filter H, where only its HLP component is transmitted. Equation (15a)* shows us that the transmitted wave will be:
CW = ½  (
(  <H|) = ¼<H| [18]
<H|) = ¼<H| [18]
Thus the source has sent out an OW of unit amplitude and has received back a CW in state
Now consider the modification of the apparatus shown in Fig. 10b in which the second filter R has been removed. Now the OW is placed in a pure state of HLP by filter H, so that when it travels to filter V it cannot be transmitted. Therefore, no OW reaches the detector D and no transaction from S to D takes place. With filter R removed the transmission of the apparatus drops from 25% to 0%.
The TI description of other experiments involving non-commuting variables can be constructed by employing the same procedures used above (see Section 4.7, for example). In each case it will be found that the probability of the quantum event under consideration is just the real and positive amplitude of the echo CW response to the OW from the emitter.
Continue on to Section 4.5
 *. The transaction will be confirmed and the photon transmitted from S to D with a probability of 1/4 and will arrive at D in a state of pure vertical polarization. There will also be a probability of 3/4 that the photon will not be transmitted to D but instead will be absorbed by one of the filters. These are the same transmission and absorption probabilities which are given by classical optics {footnote 21} for the transmission of an initially HLP beam of light from S to D.
*. The transaction will be confirmed and the photon transmitted from S to D with a probability of 1/4 and will arrive at D in a state of pure vertical polarization. There will also be a probability of 3/4 that the photon will not be transmitted to D but instead will be absorbed by one of the filters. These are the same transmission and absorption probabilities which are given by classical optics {footnote 21} for the transmission of an initially HLP beam of light from S to D.
Go back to Section 3.8
Go back to Table of Contents