between the angle settings of the two filters.
Go back to Table of Contents
Go back to Section 4.0
Continue on to Section 5.0
4.5 The Freedman-Clauser Experiment and Herbert's Paradox
As discussed in Section 1.0, the Freedman-Clauser experiment (1972) and later tests of the Bell inequality (Clauser and Shimony, 1978; Aspect, 1982a,b) have demonstrated that quantum mechanics (and nature) cannot simultaneously have the properties of CFD and locality. In the present work we advocate the view that the solution to this dichotomy is that quantum mechanical description of nature is intrinsically nonlocal. Quantum mechanics as interpreted with the TI is an explicitly nonlocal description of quantum processes. It is therefore informative to apply this description to the multi-particle quantum events of the Freedman-Clauser experiment.
We refer to Fig. 1a which was previously used in Section 2.4 in describing the FC experiment. Source S produces a pair of photons which are only allowed to leave the source if they are 180° apart and which are constrained by angular momentum conservation to be in the same state of polarization (which may be either a helicity [circular polarization] state or a linear polarization state). As discussed in Section 4.4, we can use any circular or linear basis to describe all such states.
The FC apparatus employs polarimeters consisting of linear polarizing filters placed in front of single-quantum sensitive photomultiplier detectors. The linear polarizing axes of the filters are rotated about the axis defined by the line of flight of the photons. The coincidence counting rate between photon events detected in the two photomultiplier tubes is recorded as a function of the angle settings of the two filters. This coincidence rate is expected by symmetry to depend only on the the relative angle between the angle settings of the two filters.
As discussed in Section 2.4, quantum mechanics predicts, if the filters are ideal, that the coincidence rate will be proportional to Cos2, i.e., maximum when the polarimeter axes are aligned and zero when they are at right angles. It is this deceptively innocent result which stands in violation of Bell's inequality and which implies some nonlocality in the enforcement of this correlation between separated measurements.
The analysis of this experiment with the TI will be similar to that of Section 4.4. The source S generates two correlated OW's |A1> and |B1>, which are constrained by angular momentum conservation to be in the same state of polarization, but are in an indefinite and uncollapsed state. These OW's propagate down the two arms of the apparatus until they encounter the polarizing filters FA and FB. Each filter transmits only |A2> or |B2>, the component of the OW which matches its orientation angle. These components then reach the photomultiplier tubes A and B and are absorbed. The absorption process produces CW's <A2| and <B2|, the time reverses of the incident OW's, and these propagate in the negative time direction back through the apparatus to the filters. Since each CW is in a state which matches the filter orientation, they are transmitted unmodified to the source.
Thus the source receives CW echoes <B1| and <B2| in response to the two emitted OW's. However, these responses will not, for arbitrary settings of the polarizing filters, satisfy the boundary condition that the two photons are in the same polarization state, and therefore they cannot participate fully in the formation of the transaction which is a double quantum event involving the emission and detection of both photons. Rather, as required by TI4, the transaction will project from one of these CW's only the component which matches the other and will ignore the non-matching or orthogonal component. Thus if the polarizing filters are aligned the CW's will match and there will be a maximum coincidence rate, while if the polarizing filters are at right angles the CW's will be in orthogonal states, no transaction can be formed, and the coincidence rate will be zero.
As discussed in Section 3.6 and illustrated in Fig. 5, the combination of four-vectors in such a two photon transaction provides a "bridge" across the spacelike interval between the two detection events to enforce their correlation, even though the structural members of the bridge are lightlike four-vectors which transform properly under Lorentz transformations. Thus the TI description of the FC experiment is explicitly nonlocal. But as demonstrated by several authors (Eberhard, 1976, 1978; Ghirardi, 1979, 1980), it is not possible to exploit this nonlocality for the purposes of nonlocal observer-to-observer communication.
Recently, however, Herbert (1982) has suggested a gedanken experiment which is a modification of the basic FC apparatus intended for communication. Herbert's arguments suggest that nonlocal observer-to-observer communication may be experimentally possible. A simplified version of Herbert's apparatus is illustrated in 
Fig. 11. Essentially he has added a laser "gain tube" amplifier to arm B of the FC apparatus so that the process of stimulated emission is used to "clone" the photon from the source, making multiple copies of the |B1> state vector so that its state of polarization can be definitively determined by using beam splitters to route duplicate photons to multiple measurements with polarimeters aligned along many axes. Such measurements, it is asserted, will reveal the kind of polarization measurement which was performed on |A1>, e.g., a circular polarization measurement or a linear polarization measurement. This, it is asserted, will permit an observer at arm A to "telegraph" a message to a second observer at arm B across a spacelike interval by encoding the message in the time structure of the measurements performed (e.g., as 1's and 0's in a binary code.)
To illustrate the paradox more explicitly, let us consider a simplified version of Herbert's apparatus in which (in the rest system of the apparatus) the single photon arriving in arm A is measured slightly earlier than whatever measurements occur in arm B. Moreover, we assume that the photon in arm B is duplicated once and that each photon separately is subjected to a LP measurement which determines whether it is in a horizontal (H) or a vertical (V) state of linear polarization. Herbert argues that if the "sender" at arm A has chosen the LP basis for his measurement, i.e., the same basis as that of the pair of measurements in arm B, then the photons reaching arm B will be in a pure state of linear polarization and the measurements there will always match, i.e., the measurements will always show H+H or V+V and never H+V or V+H. On the other hand, it is argued, if the sender at A uses the CP basis for his measurement then the photons reaching arm B will be in a mixed state of linear polarization and the measurements there will show matching (H+H or V+V) and non-matching (H+V or V+H) responses with equal probability. Thus a repeated sending of the message at arm A would permit its reception in arm B, even in the presence of strong spontaneous emission noise in the laser amplifier.
Herbert's arguments are implicitly based on the Copenhagen interpretation's account of state vector collapse. It is assumed that once the measurement at arm A has occurred the SV for the photons reaching arm B will have collapsed into a definite state of polarization which can then be determined to discover what A measurement had been made. This description is consistent with the Copenhagen interpretation, but it does give a special and rather unsymmetric role to one of the three measurements which are performed on the same system. This is perhaps justified by the time sequence of the measurements if the arm A measurement occurs first.
Even before Herbert's paper appeared in print there were several "refutations" published which concerned themselves with spontaneous emission noise in the stimulated emission process (Wooters, 1982; Milonni, 1982) or with the description of the quantum state which such an amplification process would produce. The former analyses are probably irrelevant to the heart of the problem, because the envisioned communication could in principle persist even in the presence of such noise. On the other hand, the analysis of Dieks (1982) seems to provide a satisfactory (if rather formal) resolution of the "paradox.
Analysis of the gedanken experiment with the TI is relatively straightforward. The transaction corresponding to each detection event must involve the absorption of all three photons and must connect loci at the source, three of the detectors, and the laser amplifier. The transaction can be verified only if all of the CW's are in non-orthogonal states. Thus the polarimeters in arm B can never record events which are H+V or V+H, no matter what measurement the sender performs, because this would generate orthogonal CW's which would not verify the overall multi-photon transaction. Therefore, even under ideal circumstances (which may not be realizable experimentally) the responses in arm B must always match and no observer-to-observer message can be transmitted. Dieks used a more detailed analysis employing the quantum mechanical formalism to arrive at the same conclusion: multiple polarimeters in arm B of the apparatus will always give matching responses, no matter what is measured in arm A.
The basic fallacy in Herbert's argument, from the viewpoint of the TI, is that he was led by the CI to assume that the measurement in arm A collapses the SV so that the apparatus in arm B is presented with a photon in a definite state, and that the correlation between arms A and B are enforced by this collapse while the correlations between the duplicate photons in arm B are not. The TI requires the enforcement of all correlations equally. There is no single measurement which collapses the SV presented to the others, but rather a transaction enforcing correlation of all measurements, independent of the time sequence in which they occur. This enforcement can only be accomplished if the measurements in arm B match not only the measurement in arm A but also match each other.
4.6 The Hanbury-Brown-Twiss Effect
The Hanbury-Brown-Twiss effect (HBT) is an example of the interference of radiation sources which are incoherent (Klauder, 1968). It has been applied to the measurement of the diameters of nearby stars with radio interferometry and to investigation of the "hot-spot" developed in a relativistic heavy ion collision in which pions are produced (Gyulassy, 1979). The effect applies equally well to classical waves and to particle-like quanta.
A simplified version of a HBT interference measurement is illustrated in 
Fig. 12. Sources 1 and 2 are separated by a distance d12. Both sources emit photons of the same energy h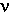
but are completely incoherent. The radiation from the two sources are detected by detectors A and B which are separated by a distance dAB. The line of centers of the sources is parallel to the line of centers of the detectors, and the two lines are separated by a distance L.
It will not be demonstrated here, but a signal which is a product of (or coincidence between) the signals received at A and B (indicating that photons have simultaneously triggered both detectors) reflects the coherent interference of the two sources and depends on the source separation d12 as well as the detector separation dAB. Measurements made at a number of values of dAB can therefore be used to determine d12, in a manner analogous to moving a single detector in an interference pattern to determine the separation of a pair of coherent sources. This is the HBT interference effect.
There is a lesson for applications of the TI in this kind of interference phenomenon: particles like photons and electrons cannot consistently be described as a blobs which travel from point A to point B. In the HBT effect a whole photon is assembled at the detector out of half-photons contributed by each of the two sources. Consider a transaction in which photons are emitted by 1 and 2 and detected by A and B so that their product signal exhibits HBT interference. In the TI description of such an HBT event, retarded OW's |x1> and |y1> are emitted by the source 1 and travel to detectors A and B , respectively. Similarly, OW's |x2> and |y2> are emitted by the source 2. Detector A receives a composite OW |A12> which is a linear superposition of |x1> and |x2> and seeks to absorb the "offered" photon by producing advanced CW <A12|, the time reverse of that superposition. Detector B similarly responds to composite OW |B12>. These advanced waves then travel back to the two sources, each of which receives a different linear superposition of <A12| and <B12|.
A HBT transaction is formed which removes one energy quantum h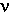 from each of the two sources 1 and 2 and delivers one energy quantum h 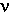to each of the two detectors A and B. For many combinations of source and detector separation distances, the superimposed OW's and/or CW's are nearly equal and opposite, so that the composite wave is very weak and the transaction is very improbable. For a few ideal combinations of source and detector separation distances all of the composite waves are strong because their components coherently reinforce, and in this case the transaction is much more probable. The transaction probability depends on the separation distances in just the way predicted by quantum mechanics. Thus the HBT effect is completely consistent with the TI.
However, there is an interesting point here: neither of the photons detected by A or B can be said to have uniquely originated in one of the two sources. Each detected photon originated partly in each of the two sources. It might be said that each source produced two fractional photons and that fractions from two sources combined at a detector to make a full size photon. This is what TI4 emphasized in stating that "Particles transferred have no separate identity which is independent from the satisfaction of those (the quantum mechanical) boundary conditions." The boundary conditions here are those imposed by the HBT geometry and detection criteria.
This two photon event may be viewed as a simple case of more general multiphoton (or multiparticle) events, which may involve many sources and many detectors. Such transactions can be viewed as assembling particles at a detector from contributions derived from an number of sources, with no one-to-one correspondence between particles emitted and particles detected except in overall number. One way of stating this is to emphasize that the the spatial localization of the emitter (or the absorber) may be very fuzzy and indefinite, so long as all boundary conditions are satisfied. Likewise the time localization of the emission event (or absorption event) can be made very indefinite by a choice of experimental conditions, e.g., very low emission probability as in the Pflegor-Mandel experiment (1975).
4.7 The Albert-Aharonov-D'Amato Predictions
The predictions of Albert, Aharonov, and D'Amato (1985) clarify an old problem, the question of retrospective knowledge of a quantum state following successive measurements of non-commuting variables (Aharonov, 1963). The assumption of contra-factual definiteness (CFD) mentioned in the introduction (Section 1.0) plays an important role in the Albert, Aharonov and D'Amato (AAD) predictions because these concern the retrospective knowledge of the observer about the outcome of experiments which might have been performed on the system in the time interval between one of the measurements and the other. We need the CFD assumptions that the various alternative possible measurements which might have been performed on the system would each have produced a definite (although unknown and possibly random) observational result and that we are permitted to discuss these results. Under the assumption of CFD, the AAD predictions provide a challenging QM interpretational problem.
As a simple example of the AAD predictions, consider the experiment illustrated in 
Fig. 13a. A photon is emitted from source S and is transmitted through a filter H which passes only horizontal linearly polarized (HLP) light. It then travels a distance L and is transmitted through a second filter R which passes only right circularly polarized (RCP) light. The photon is then detected by a quantum sensitive photomultiplier tube D which generates an electrical signal registering the arrival of the photon. The questions which are addressed by AAD are: (1) What is the quantum state of the photon in the region L which lies in the region between H and R, and (2) What would have been the outcome of measurements on the photon which might have been performed in that region?
The authors of AAD use the formalism of quantum mechanics as applied to the joint probability of a series of measurements (Aharonov, 1964) to demonstrate a remarkable pair of predictions (here applied to the present example): (1) if a linear polarization measurement had been performed (Fig. 13b) in region L the photon would have been found to be in a HLP state, and (2) if a circular polarization measurement (Fig. 13c) had been performed in region L the photon would have been found to be in a RCP state. In other words the intermediate measurement of polarization appears to be equally influenced by the past linear polarization measurement which was performed at H and by the future circular polarization measurement which will be performed at R, in that both seem to equally prepare the system in a definite state which "forces" the outcome of the intermediate measurement.
This completely valid application of the QM formalism appears to be in at least interpretational conflict with the uncertainty principle (CI1) and with complementarity (CI3), which assert that since RCP and HLP states are eigenstates of noncommuting variables, a photon cannot have been in both of these eigenstates simultaneously. The authors of AAD, on the other hand, interpret their result as indicating that "without violating the statistical predictions of quantum mechanics, it can be consistently supposed ... that non-commuting observables can simultaneously be well defined" and that indeed, "given those statistical predictions, ... it is inconsistent to suppose anything else". The AAD result has been summarized in a popular account (S&TC, 1985) as indicating that: "The measurement on Friday caused, in some sense of the word cause, the smeared-out values of spin on Wednesday to collapse into some definite configuration. The logical puzzle about time and causality that this development engenders has not yet been fully explored."
It is therefore of considerable interest to apply the TI to this new interpretational puzzle, both as a means of gaining insight into the problem and as a test of the utility of the TI for resolving the interpretational paradoxes of quantum mechanics. The TI analysis of this problem follows that of Section 4.4 which also dealt with the transmission of a photon through polarizing filters. The three experimental configurations considered are illustrated in Figs. 13a-c, and 
Figs. 14a-c show diagrammatically the corresponding SV descriptions which will be discussed. These experimental configurations must be treated as separate (but related) quantum mechanical systems and each must be analysed separately with the TI. Let us first consider Fig. 13b.
The TI provides the following description of the transmission of the photon from S to D with an intermediate HLP measurement: The source S produces a retarded OW in the form of a general SV including all possible states of polarization. This wave then passes through filter H. The filter transmit only |H>, i.e., that component of the SV which corresponds to a state of pure horizontal linear polarization (HLP). This wave then travels to filter H1, which transmits |H> unchanged. This HLP wave then travels to filter R, which transmits only that component which is in a pure state of right circular polarization (RCP). From equation (15c), this will be 
|R>. This RCP wave then strikes the photocathode of D and is absorbed and detected, producing the advanced wave <R|, the CW which travels back along the track of the incident OW to confirm the transaction. When the CW reaches R it is transmitted without modification because it is already in a state of RCP. However, when it reaches H1, only its HLP component is transmitted, so from equation (15a) it becomes (<H|)=½<H|. It retains this form as it passes through the filter H and back to the source S.
The description of the transmission of the photon from S to D with an intermediate RCP measurement illustrated in Fig. 13c is very similar: The source S produces a retarded OW in the form of a general SV including all possible states of polarization. This wave then passes through filter H which transmits only |H>. This wave then travels to filter R1, which transmits only that component which is in a pure state of right circular polarization (RCP). From equation (15c), this will be |R>. This RCP wave then travels to filter R, which transmits |R> unchanged. It strikes the photocathode of D and is absorbed and detected, producing the advanced wave <R|, the CW which travels back along the track of the incident OW to confirm the transaction. When the CW reaches R and R1 it is transmitted without modification because it is already in a state of RCP. However, when it reaches H, only its HLP component is transmitted, so from equation (15a) it becomes (<H|)=½<H|. It retains this form as it passes back to the source S.
In cases (b) and (c) the insertion of the intermediate polarizing filter does not alter the statistical aspects of the measurement from that of case (a) where there is no intermediate measurement, and so the three cases are equivalent in the observational sense. However, the TI gives us the opportunity to examine the intermediate quantum states in each case, and when this is done we find that the transaction which is confirmed is quite different in each of the three cases. This is illustrated in Fig. 14. In case (a) where there is no intermediate measurement the state in the intermediate region between H and R is in an indeterminate quantum state, in that the OW is |H> while the CW is <R|. This is also the case for the region between H1 and R for case (b) and for the region between H and R1 for case (c). However, we see that for case (b) the photon in the region between H and H1 is in a state of pure HLP (circled), while for case (c) the photon between R1 and R is in a state of pure RCP (circled).
The TI resolution of the riddle posed by the AAD predictions is that the uncertainty principle is not compromised, nor can non-commuting observables simultaneously be well defined, as the AAD authors have suggested. However, as was suggested above in another context, the circular polarization measurement which occurs later at R does cause, in some sense of the word cause, the smeared-out values of circular polarization between R and H to earlier "collapse into some definite configuration". The transactions which form in the three cases are not identical, even though they have the same observables, because each transaction is a separate self consistent solution to the wave equation. Each satisfies a different set of boundary conditions. The insertion of the intermediate filter, while not altering the statistics of the measurement, brings into being a different transaction which has different characteristic eigenstates in the intermediate region between H and R. Thus the two predictions of the AAD calculation concern intrinsically different quantum systems and cannot be construed as implying the presence "simultaneously" of the eigenstates of no-commuting variables.
Continue on to Section 5.0
Go back to Section 4.0
Go back to Table of Contents