Go back to Table of Contents
Go back to Section 3.3
Continue to Section 4
The Transactional Interpretation of Quantum Mechanics
by John G. Cramer
3.8 Completeness and Predictivity in the Transactional Interpretation
As was shown in Section 2.5, the solution of the problem of completeness posed in the EPR paper is implicit in the formalism of quantum mechanics, provided the SV is interpreted as a real physical quantity. Since the TI treats the SV as a real physical quantity, quantum mechanics as interpreted with the TI is a complete theory. In particular, the SV brings to each potential absorber the full range of possible outcomes and all have "simultaneous reality" in the EPR sense. The absorber interacts so as to cause one of these outcomes to emerge in the transaction, so that the collapsed SV manifests only one of these outcomes. And the quantum mechanical formalism insures that if one of a pair of canonically conjugate quantities is localized in such a transaction, the other quantity is correspondingly de-localized as required by the uncertainty principle.
The TI also clarifies, but does not solve, the problem of predictivity. As was discussed in Section 3.2, the beginning of a transaction can be viewed as the emitter sending out a retarded "offer" wave in various directions and receiving an "echo" back from the absorber in the form of an advanced confirmation wave which has an amplitude proportional to  * (where
* (where  is the complex OW evaluated at the absorber locus). In the usual circumstance there are a very large number of potential future absorbers, and if all provide such echoes, the emitter, at the instant of emission, has a large menu of possible transaction possibilities from which to choose. In a single quantum event the boundary conditions will permit only one event to occur.
is the complex OW evaluated at the absorber locus). In the usual circumstance there are a very large number of potential future absorbers, and if all provide such echoes, the emitter, at the instant of emission, has a large menu of possible transaction possibilities from which to choose. In a single quantum event the boundary conditions will permit only one event to occur.
Born's probability law is therefore a statement that the probability of occurrence of a given transaction is proportional to the magnitude of the echo corresponding to that transaction which the emitter receives. This would seem to be a very plausible assumption. The quantum event, from this point of view, is a solution to a differential equation (the appropriate wave equation) for which a definite set of boundary conditions restrict the solutions but do not uniquely specify the solution. In this situation, the probability of a given solution is proportional to the "connectedness" of the participants as indicated by the size of the echo which the absorber sends back to the emitter. The emitter is presented with echoes from potential absorbers which form a weighted list of possible transactions, from which only one may be chosen. The future absorbers can influence the past emission event only through the strength of their echo entry on this list but cannot influence which entry is actually chosen for the transaction.
We note that there are analogous classical situations in which a system is specified by a set of differential equations with incompletely specified boundary conditions, for example, in the fluid dynamics of turbulent flow. And interestingly enough, there has been significant recent progress in these fields through the application of new mathematical techniques such as catastrophe theory, the theory of strange attractors, etc. It seems possible that similar techniques might some day be applied to the statistical processes of quantum mechanics.
And so while the TI does not alter the essentially statistical character of quantum mechanics it has provided a glimpse of the "dice" which are at work in the statistical processes. The dice work to ensure an outcome consistent with the quantum boundary conditions of a transaction and are "loaded" in proportion to the magnitude of the echo which the emitter receives from potential absorbers.
3.9 Relativity and Causality in the Transactional Interpretation
Several times we have mentioned the related constraints of nonlocality, relativistic invariance, and causality. As was previously mentioned it would seem that the nonlocality of the transaction as defined above would give severe problems with both of the latter constraints by permitting both simultaneity tests across spacelike intervals and backward-in-time communication. However, this is not the case, as we shall show here.
The emitter-absorption transaction, although it has the effect of enforcing nonlocal correlations between separated parts of a system, cannot be used for nonlocal communication between observers. There are no residual advanced effects when the transaction is complete, and the reinterpretation of the advanced waves insures that the result is observationally the same as if only retarded waves were present. Further, as has been shown mathematically (Eberhard, 1976, 1978; Ghirardi, 1979, 1980; Mittelstaedt, 1983), the nature of the correlations enforced between the separated parts of a FC experiment is such as to preclude the possibility of nonlocal communication between observers.
Since the transaction is atemporal, forming along the entire interval separating emission locus from absorption locus "at once", it makes no difference to the outcome or the TI description if separated experiments occur "simultaneously" or in any time sequence. There is likewise no issue of which of the separated measurements occurs first and precipitates the SV collapse, since in the TI both measurements participate equally and symmetrically in the formation of the transaction. Further, the paths across which the correlation enforcing exchange takes place are lightlike four-vectors and remain so under any Lorentz transformation. Therefore, the outcome and the TI description of any correlation experiment is the same independent of the inertial reference frame from which it is viewed, as it must be if quantum mechanics and relativity are to be compatible theories.
The obvious "backwards in time" character of the transaction model warrants careful consideration of whether causality is preserved. In a sense the TI tells us that absorber "causes" the transaction which precedes it in time sequence, in violation of cause-before-effect. To come to terms with this aspect of the TI it is necessary to carefully consider the nature of causality and the physical evidence which supports it. In a previous paper (Cramer, 1980) we have made the distinction between the strong principle of causality, which asserts that a cause must always precede its effect in any reference frame, and the weak principle of causality, which asserts the same thing, but only as it applies to macroscopic observations and to observer to observer communication. There is no present experimental evidence in support of any causal principle which is stronger than the weak principle.
The TI is completely consistent with the weak principle of causality. As discussed previously, the completion of the transaction removes all interacting advanced fields except the one connecting emitter with absorber, and the remaining advanced/retarded superposition can be reinterpreted as purely retarded. Thus there are no "advanced effects", no evident acausal behavior even at the microscopic level. Dispersion relations, etc., are completely consistent with microcausality as it is conventionally interpreted.
Nature, in a very subtle way, may be engaging in backwards-in-time handshaking. But the use of this mechanism is not available to experimental investigators even at the microscopic level. The completed transaction erases all advanced effects, so that no advanced wave signalling is possible. The future can effect the past only very indirectly, by offering possibilities for transactions.
3.10 The Arrow of Time in the Transactional Interpretation
The formalism of quantum mechanics, at least in its relativistically invariant formulation, is completely even handed in dealing with the "arrow" of time, the distinction between future and past time directions. Even the apparently asymmetric action of an ideal macroscopic measurement in "preparing" a system in a definite quantum mechanical state can be formally described in the context of the probability interpretation in a completely time symmetric way (Aharonov, 1964).
In the discussion of the CI in Section 2.3 the point was made that the description of collapse in the CI is intrinsically unsymmetric in time. The transaction model of Section 3.2 gives the appearance of being more symmetrical, in that it treats past emitter and future absorber as equal terminators of the transaction which develops between them. However, the careful reader will perceive that there is a more subtle time asymmetry implicit in the TI description of the quantum event which is implicit in TI2. There the probability of a quantum event with emission from (R1,T1) to an absorber at (R2,T2) is assumed to be:
P12 = | 1(R2,T2)|2 [12]
1(R2,T2)|2 [12]
rather than:
P12 = | 2(R1,T1)|2 [13]
2(R1,T1)|2 [13]
i.e., in the TI the emitter is given a privileged role because it is the echo received by the emitter which precipitates the transaction rather than that received by the absorber. Thus the past determines the future (in a statistical way) rather than the future determining the past.
Assumption [12] is consistent with the usual formulation of quantum mechanics, the "post" formulation, which employs this rule in the evaluation of event probabilities. The alternative "prior" formulation, which employs [13] to evaluate probabilities, is rarely used but in the absence of violations of time reversal invariance must give the same result for an exact calculation (DeVries, 1974).
This symmetry between the post and prior formulations and the equivalent symmetry between post and prior versions of the TI based on [12] and [13] might be taken as a sufficient even-handedness in the handling micro-reversibility, except for the one problem. Nature has exhibited a clear violation of time reversal invariance at the microscopic level in the decay of the K0L meson. From experimental investigations of the CP-violating decay modes of the K0L system, it is inferred that the time direction of the reaction K0L + e+ =>  + +
+ + 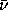 will be apparent in its cross section, i.e., the inverse reaction will have a qualitatively different reduced cross section from that of the forward reaction. It is not possible to provide a fixed target of any of the particles participating in this reaction, and therefore it is not experimentally feasible to directly observe either of these reaction modes. Therefore this should be considered as a gedanken experiment. But even at that, it implies that the post and prior formalisms and interpretations are in principle distinguishable and therefore not equivalent.
will be apparent in its cross section, i.e., the inverse reaction will have a qualitatively different reduced cross section from that of the forward reaction. It is not possible to provide a fixed target of any of the particles participating in this reaction, and therefore it is not experimentally feasible to directly observe either of these reaction modes. Therefore this should be considered as a gedanken experiment. But even at that, it implies that the post and prior formalisms and interpretations are in principle distinguishable and therefore not equivalent.
The work of Aharonov, et al (1964) mentioned above showed that for ideal systems and measurements a plausible time-symmetric probability interpretation could be formulated to replace the usual one of Born (CI2). However, they found that in order to use this rule in a way which gave the same QM predictions as those of the conventional probability law, they were forced to employ a time asymmetric side-condition on its use. Belinfante (1975) expanded this analysis to include non-ideal measurements and systems and found that the importance of time asymmetries was even more apparent in the more general case. This body of work leads to conclusions similar to those which have stated above concerning the existence and inevitability of a quantum mechanical arrow of time.
This microscopic quantum mechanical arrow of time must be accounted for. Fortunately, a justification of such a time asymmetry has already been accomplished for the case of WF electrodynamics by the author in a previous publication (Cramer, 1983). A boundary condition model of the T=0 Big Bang was used to relate the electromagnetic arrow of time (the macroscopic dominance of retarded electromagnetic radiation) to the cosmological arrow of time (the direction of expansion of the universe). The arguments presented in that paper apply equally to the transaction model presented here and justify the use of probability law [12] rather than [13].
Continue to Section 4
Go back to Section 3.3
Go back to Table of Contents
 * (where
* (where  is the complex OW evaluated at the absorber locus). In the usual circumstance there are a very large number of potential future absorbers, and if all provide such echoes, the emitter, at the instant of emission, has a large menu of possible transaction possibilities from which to choose. In a single quantum event the boundary conditions will permit only one event to occur.
is the complex OW evaluated at the absorber locus). In the usual circumstance there are a very large number of potential future absorbers, and if all provide such echoes, the emitter, at the instant of emission, has a large menu of possible transaction possibilities from which to choose. In a single quantum event the boundary conditions will permit only one event to occur.
 + +
+ + 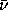 will be apparent in its cross section, i.e., the inverse reaction will have a qualitatively different reduced cross section from that of the forward reaction. It is not possible to provide a fixed target of any of the particles participating in this reaction, and therefore it is not experimentally feasible to directly observe either of these reaction modes. Therefore this should be considered as a gedanken experiment. But even at that, it implies that the post and prior formalisms and interpretations are in principle distinguishable and therefore not equivalent.
will be apparent in its cross section, i.e., the inverse reaction will have a qualitatively different reduced cross section from that of the forward reaction. It is not possible to provide a fixed target of any of the particles participating in this reaction, and therefore it is not experimentally feasible to directly observe either of these reaction modes. Therefore this should be considered as a gedanken experiment. But even at that, it implies that the post and prior formalisms and interpretations are in principle distinguishable and therefore not equivalent.