 c]2
c]2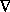 2
2 = [
= [ 2]d2
2]d2 /dt2. [8]
/dt2. [8]
Go back to Table of Contents
Go back to Section 3.0
Continue to Section 3.8
3.3 The Transactional Model and Relativistic Quantum Mechanics
The transaction model discussed in the previous section deals with the emission and absorption of photons arising from electromagnetic interactions. The model uses advanced and retarded wave functions which are solutions of the electromagnetic wave equation:
[ c]2
c]2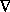 2
2 = [
= [ 2]d2
2]d2 /dt2. [8]
/dt2. [8]
Note that this differential equation is second order in the time variable. As was shown in a previous publication of the author (Cramer, 1980), the same transaction model can be applied to the emission and absorption of massive particles, either neutral or electrically charged, e.g., electrons {footnote 16}. The only requirement for this application is that the wave equations describing the particles of interest must, like the electromagnetic wave equation, have both advanced and retarded solutions.
This requirement would seem to present a problem. The wave equation which has been the focus of most of the discussion surrounding the interpretation of quantum mechanics is the Schrödinger equation:
-( 2/2m)
2/2m)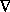 2
2 = i
= i d
d /dt, [9]
/dt, [9]
where m is the mass of the particle described by the equation. This equation is first order in the time variable and for this reason does not have advanced solutions. Therefore, if  =F(r,t) is a solution of the Schrödinger equation, then
=F(r,t) is a solution of the Schrödinger equation, then  *=G(r,t) is not a solution, nor is a linear combination of F and G as used in the transactional model.
*=G(r,t) is not a solution, nor is a linear combination of F and G as used in the transactional model.
We must bear in mind, however, that the Schrödinger equation is ultimately not physically correct because it is not relativistically invariant {footnote 17}. It should properly be considered as the limiting case, in a restricted non-relativistic domain, of some more physically reasonable relativistically invariant wave equation, e.g., the Dirac equation or the Klein-Gordon equation. These relativistic equations, like the electromagnetic wave equation, have both advanced and retarded solutions {footnote 18}.
Considering the Schrödinger equation as a limiting case, the apparent problem created by its lack of advanced solutions can be resolved. When a suitable relativistic wave equations is reduced to the Schrödinger equation by taking a non-relativistic limit (Bjorken, 1964), the reduction procedure leads to two distinct equations, the Schrödinger equation and another equation of the form:
-( 2/2M)
2/2M)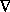 2
2 = -i
= -i d
d /dt, [10]
/dt, [10]
which is the complex conjugate or time reverse of the Schrödinger equation. This equation has only advanced solutions. Equations (9) and (10) are equally valid non-relativistic reductions of relativistic dynamics, but equation (10) is usually dropped because it has negative energy eigenvalues. From this it should be clear that F(r,t) and G(r,t) (or  and
and  *) are equally valid solutions of the dynamics which underlies the Schrödinger equation. It is therefore valid to use advanced solutions in the transactional model in the non-relativistic limit as if they were solutions of the Schrödinger equation.
*) are equally valid solutions of the dynamics which underlies the Schrödinger equation. It is therefore valid to use advanced solutions in the transactional model in the non-relativistic limit as if they were solutions of the Schrödinger equation.
We can also look at the need for relativistic invariance in another way. The interpretational problem of Locality (see Section 2.4) which the recent tests of Bell's inequality have brought into sharp focus is essentially a relativistic problem. If the velocity of light were infinite the locality problem would not exist: there would be no difference between local and non-local descriptions. The Schrödinger equation can be considered as the limiting case of a relativistically invariant wave equation when the velocity of light goes to infinity. Therefore it is not particularly surprising that an explicitly non-local description such as the transactional model may have intrinsic inconsistencies with the Schrödinger equation and may require certain properties of relativistically invariant wave equations. This is a subtle link between relativity and quantum mechanics which has not, perhaps, been previously appreciated.
There is another implication of relativistic quantum mechanics which should also be discussed here. In the relativistic domain the uncertainty principle of Heisenberg (CI1) must be reconsidered because of the added restrictions of special relativity (Landau, 1931; Berestetskii, 1971). In particular, introduction of the limiting velocity c imposes a new uncertainty relation on the precision with which momentum p can be measured: 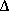 p=
p= /(c
/(c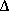 t). This relation can be considered to arise from the fact that the position localization
t). This relation can be considered to arise from the fact that the position localization 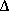 q (assumed to initially be small) cannot spread at a rate greater than c. The distance c
q (assumed to initially be small) cannot spread at a rate greater than c. The distance c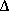 t is therefore the maximum possible amount by which the position localization can have been broadened in a time interval
t is therefore the maximum possible amount by which the position localization can have been broadened in a time interval 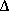 t to permit a smaller localization of momentum. This places a limit on the precision
t to permit a smaller localization of momentum. This places a limit on the precision 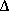 p with which momentum p can be measured in a time interval
p with which momentum p can be measured in a time interval 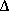 t.
t.
There is an analogous limitation on the determination of position q which arises from another characteristic of relativistic quantum field theories. As mentioned above, the solutions to the relativistically invariant wave equations for massive particles include advanced or negative frequency solutions. When a particle is localized to a sufficiently small region of space, these negative frequency functions appear explicitly in the expansion of its position wave packet. Landau and Peierls (1931) have suggested that in order to avoid the inclusion of "physically meaningless" negative frequency solutions it is reasonable to confine position determinations to a domain which does not include such processes. This corresponds to a limiting position uncertainty of 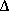 q=
q= c/W where W is the total mass-energy of the particle. This position uncertainty limit for a particle of mass m with an initially small momentum is just
c/W where W is the total mass-energy of the particle. This position uncertainty limit for a particle of mass m with an initially small momentum is just 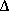 q=
q= /mc, the de Broglie wavelength of the particle.
/mc, the de Broglie wavelength of the particle.
Berestetskii, et al (1971) justify this limit on position localization in a related but slightly different way. They interpret the negative frequency or negative energy components of the wave function as indicating the onset of particle-antiparticle production when the momentum becomes large enough to correspond to a free energy greater than 2mc2. They argue that when this threshold is reached in a measurement, for example in determining the position of an electron, "the formation of new particles in a way which cannot be detected by the process itself clearly renders meaningless the measurement of the electron coordinates". Thus the broadening in momentum is cut off at this limit, leading to the  c/W limit on the position localization.
c/W limit on the position localization.
Landau and Peierls (1931) have argued that these relativistic limits on determinations of position and momentum irretrievably compromise the utility of these dynamical variables for measurement in the sense of non-relativistic quantum mechanics. Neither the position nor the momentum of a particle can, even in principle, be determined to arbitrary accuracy in a finite time interval nor can either be considered to have a particular value at a particular time. This would seem, in effect, to invalidate Born's statistical interpretation of quantum mechanics (CI2), in that the description of the state vector as a mathematical representation of the probability of finding a definite value of a particular observable as a result of a measurement made at a given instant is untenable. However, Bohr and Rosenfeld (1933; see also Rosenfeld, 1955) defused this problem by demonstrating that in the relativistic formalism of quantum electrodynamics, in which the field quantities are not represented by point functions but by functions of space time regions, there is no discrepancy between limits imposed by the relativistic uncertainty principle and the physical possibilities of measurement.
To put it slightly differently, this is a non-problem. The relativistic limits on the precision with which dynamic variables can be measured do indeed make these variables less directly relevant to the coordinates of relativistic particles. However, this invalidates neither their use nor their usefulness. In a related non-relativistic case the angle of rotation  remains a valid and sometimes useful dynamical variable although its measurable value is rendered completely uncertain by quantization of the conjugate angular momentum variable. The specification of a dynamical variable "at a given instant" as considered by Landau and Peierls (1931) is neither needed nor desirable. In the relativistic formalism it is integrals over spacetime regions rather than point values which lead to the predictions of observables. In this context, the atemporal and non-local character of the transactional interpretation as discussed below provides a natural way of describing the atemporal collapse of the state vector to some localized value of a dynamic variable. In fact, the notion that the state vector collapses to a particular value of a variable "at a given instant" is inconsistent with the transactional description. See Section 4.3, for example, for discussion of this point.
remains a valid and sometimes useful dynamical variable although its measurable value is rendered completely uncertain by quantization of the conjugate angular momentum variable. The specification of a dynamical variable "at a given instant" as considered by Landau and Peierls (1931) is neither needed nor desirable. In the relativistic formalism it is integrals over spacetime regions rather than point values which lead to the predictions of observables. In this context, the atemporal and non-local character of the transactional interpretation as discussed below provides a natural way of describing the atemporal collapse of the state vector to some localized value of a dynamic variable. In fact, the notion that the state vector collapses to a particular value of a variable "at a given instant" is inconsistent with the transactional description. See Section 4.3, for example, for discussion of this point.
Another problem which raises some concern about the statistical interpretation of quantum mechanics in the relativistic domain is the observation that the solutions of the field equations cannot always be used to construct a relativistically invariant or positive definite probability density (Bjorken, 1964). Thus, while differential field equations and their solutions remain an indispensible feature of relativistic quantum field theory (Bjorken, 1965), the problem of the identity of these solutions (see Section 2.1) is made more severe because the statistical interpretation, at least in its simplest form, has proved inadequate. The state vector cannot be identified as a simple carrier of probability in the relativistic domain.
The naive statement of the statistical interpretation is clearly insufficient in the relativistic domain, particularly when applied to space-time regions where no measurement is actually made. Further, some of the formal procedures of non-relativistic quantum mechanics, e.g., the integration of wave function products over a large volume of space at a fixed time, are manifestly inconsistent with special relativity. However, the development of relativistic quantum theory has resulted in a formalism with calculational procedures which are appropriate to the relativistic domain. A generalized form of the statistical interpretation is implicit in these procedures for calculation of observables and matrix elements. It is therefore our view that the statistical interpretation should be (and has been) generalized for the relativistic domain rather than discarded.
The scope of the present paper is limited to the interpretation of quantum mechanics in the low-velocity non-relativistic limit, the arena where almost all of the previous discussion on the interpretation of quantum mechanics has been focussed. For this reason we will not further discuss the interpretation of relativistic quantum mechanics. However, we are not aware of any new interpretational problems which are added by a fully relativistic quantum field theory beyond those associated with particle creation and space-time delocalization as just discussed. The transactional interpretation of quantum mechanics presented in the next section is based on solutions of relativistically invariant differential field equations, is fully consistent with special relativity, and seems to accommodate these additional features of a relativistic quantum theory in a very natural way. We are therefore confident that the interpretation presented here, perhaps with minor embellishments, is appropriate for the interpretation of a fully relativistic theory of quantum mechanics.
3.4 The Transactional Interpretation
Now we are prepared to specify the premises of the transactional interpretation (TI). In doing this we will use a framework which is as similar as possible to the description of the Copenhagen interpretation given in Section 2.0. We will similarly use five principle elements which we enumerate here:

 *. This will be discussed further in Section 3.8, where the character of randomness in QM is examined.
*. This will be discussed further in Section 3.8, where the character of randomness in QM is examined.
In summary, the TI adopts the first two elements of the CI and is also able to accommodate aspects of CI3. It drops the assertion of CI4 that the solutions of a simple second order differential equation relating mass, energy, and momentum are somehow related to "knowledge", and instead employs a usually neglected solution of that equation to construct the emitter-absorber transaction of TI4. The TI drops the positivism of CI5 because the positivist curtain is no longer needed to hide the nonlocal backstage machinery.
It should also be pointed out that the substitution TI4 for CI4, in giving objective reality to the state vector, colors all of the other elements of the interpretation. Although the uncertainty principle (TI1) and the statistical interpretation (TI2) are formally the same as in the CI, their philosophical implications, about which so much has been written from the viewpoint of the Copenhagen interpretation, may be rather different.
3.5 The Transactional Interpretation and the Formal Notation of QM
Comparison of the formal notation used in quantum wave mechanics with the description of the transaction model as discussed in Section 3.2 shows an excellent correspondence between the two. Once the TI is in firm conceptual grasp, the TI description of quantum processes can be perceived in the mathematical procedures and notations used in the calculation of observables. In particular, the QM formalism makes extensive use of the operation of complex conjugation. For simple systems this operation is equivalent to the operation of time reversal (Wigner, 1950) which transforms retarded waves into advanced waves {footnote 16}. Thus  * is the advanced confirmation wave (CW) equivalent of
* is the advanced confirmation wave (CW) equivalent of  , the retarded offer wave (OW). As mentioned above,
, the retarded offer wave (OW). As mentioned above, 
 * is the offer-confirmation wave echo which the emitter receives from a particular direction. Similarly,
* is the offer-confirmation wave echo which the emitter receives from a particular direction. Similarly,
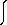 vol
vol 
 *dv [11a]
*dv [11a]
is the sum of all such OW-CW echoes from all possible locations in space.
Let us consider other examples. A QM "overlap integral" of the form
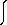 vol
vol  1
1 2*dv [11b]
2*dv [11b]
can be interpreted in the TI as representing an average over all space of the "echoes" which an emitter sending out OW  1 receives from all possible absorbers sending back CW's which confirm transactions involving a final state described by
1 receives from all possible absorbers sending back CW's which confirm transactions involving a final state described by  2. Moreover, the calculation of an expectation value of the variable x which is deduced from a given wave function
2. Moreover, the calculation of an expectation value of the variable x which is deduced from a given wave function  by the operator X, so that X
by the operator X, so that X = x
= x , has the form:
, has the form:
<x> = 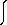 vol
vol  2* X
2* X  1 dv. [11c]
1 dv. [11c]
This can be viewed as an average over space of the possible values of x which the operator X projects from the components of the OW which appear in the completed transaction. This interpretational approach can also be applied to other aspects of the QM formalism.
From one point of view the transactional interpretation is so apparent in the Schrödinger-Dirac form of the QM formalism, with its combinations of normal and time-reversed waves, that one might fairly ask why this obvious interpretation of the QM formalism had not been previously made. No one can, of course, explain why something did not occur in the history of the development of quantum physics, but several relevant observations can be made:
 * with advanced solutions of the wave equation is by no means obvious;
* with advanced solutions of the wave equation is by no means obvious;
 * of the formalism. Appendix A.5 discusses the few previous attempts to use advanced waves in QM interpretation.
* of the formalism. Appendix A.5 discusses the few previous attempts to use advanced waves in QM interpretation.
3.6. Identity and Complexity in the Transactional Interpretation
In dealing with the problem of identity, TI2 gives the SV the same meaning as did CI2, as the medium for describing the probability of various possible quantum events. TI4 deals more directly with the problem of identity and deals with it in a way which is quite different from that of CI4. It asserts that the state vector is a real physical wave which is generated by the emitter and travels through space to the final absorber and also to many other space-time loci and to many other potential absorbers. The state vector is the "offer wave" which initiates the transaction. Because of the quantum mechanical boundary conditions the transaction is only completed between a single emitter and absorber in a one-quantum event. The particle itself (photon, electron ,etc.) is not identical with the state vector but with the completed transaction, of which the state vector is only the initial phase.
Schrödinger's {footnote 11} original attempt to interpret the state vector in a way similar to this was unsuccessful because of two problems:
Since the TI considers the SV to be physically present in space it must deal directly with the problem of complexity. However, the transaction model is able to do this because at each point of the completed transaction at which there is a physical interaction, e.g., at the emitter and absorber loci, there is also a superposition of an advanced and a retarded wave of equal amplitude. Since  +
+  * = 2Re(
* = 2Re( ), the collapsed SV becomes real, and there is no residual imaginary part of the SV to require explanation. The reader is referred to Section 4.4 for a detailed example showing the real net amplitude from a transaction. In regions of space where there was no interaction, the SV is permitted to be complex, but these components are "virtual" and non-interactive since they produce no transfer of energy or momentum. Thus, the TI has restored algebraic reality to the description of the microcosm.
), the collapsed SV becomes real, and there is no residual imaginary part of the SV to require explanation. The reader is referred to Section 4.4 for a detailed example showing the real net amplitude from a transaction. In regions of space where there was no interaction, the SV is permitted to be complex, but these components are "virtual" and non-interactive since they produce no transfer of energy or momentum. Thus, the TI has restored algebraic reality to the description of the microcosm.
3.7 Collapse and Nonlocality in the Transactional Interpretation
In the TI the collapse of the state vector is interpreted as the completion of the transaction started by the OW and the CW exchanged between emitter and absorber. The emergence of the transaction from the SV does not occur at some particular location in space or at some particular instant of time, but rather forms along the entire four-vector which connects the emission locus with the absorption locus (or loci in the case of multiple correlated particles). The transaction employs both retarded and advanced waves which propagate, respectively, along positive and negative lightlike (or timelike) four-vectors. Since the sum of these four-vectors can span spacelike and negative timelike or lightlike intervals, the "influence" of the transaction in enforcing the correlations of the quantum event is explicitly both nonlocal and atemporal.
![]() Fig. 5 shows an example of such combinations of four-vector for a two photon transaction corresponding to an event in the Freedman-Clauser experiment. Note that although all of the waves in the transaction lie along lightlike world lines, the "influence" which enforces the correlations between the two polarization measurements spans a spacelike interval and is therefore nonlocal. This nonlocality is an explicit feature of the TI arising from the use of advanced waves.
Fig. 5 shows an example of such combinations of four-vector for a two photon transaction corresponding to an event in the Freedman-Clauser experiment. Note that although all of the waves in the transaction lie along lightlike world lines, the "influence" which enforces the correlations between the two polarization measurements spans a spacelike interval and is therefore nonlocal. This nonlocality is an explicit feature of the TI arising from the use of advanced waves.
Schrödinger (1935), in analyzing the EPR paradox, concluded that at least part of the problem lay in the way time is used in quantum mechanics (in the context of the CI). The CI treats time in an essentially classical non-relativistic way, and as we have seen in Section 2.5, this leads to inconsistencies with relativity or causality in any non-subjective CI description of collapse in, for example, the Freedman-Clauser experiment. The root of the inconsistencies lies in the implicit assumption of the CI that the SV collapse occurs at a particular instant at which a particular measurement is made and "knowledge" is gained, that before this instant the SV is in its full uncollapsed state, and that there can be a well-defined "before" and "after" in the collapse description. In the TI the collapse, i.e., the development of the transaction, is atemporal and thus avoids the contradictions and inconsistencies implicit in any time-localized SV collapse.
Further, the TI description does not need to invoke arbitrary collapse triggers such as consciousness, etc., because it is the absorber rather than the observer which precipitates the collapse of the SV, and this can occur atemporally and nonlocally across any sort of interval between elements of the measuring apparatus. This will be discussed further in the context of gedanken experiments in Section 4.
Continue to Section 3.8
Go back to Section 3.0
Go back to Table of Contents