Size of the atomic nucleus: Rutherford Scattering
1.9. Size of the atomic nucleus: Rutherford Scattering#
The evidence that most of the mass of an atom is in the nucleus comes from the Rutherford experiment. In this experiment alpha-particles are scattered from a gold foil. The vast majority of the alpha-particles pass straight through the foil and are deflected from their original trajectory by only a small amount. A small number alpha particles are scattered backwards by the foil travelling back along their original trajectory. This suggests that the mass of an atom is concentrated in a very small volume.
Rutherford scattering is caused by the Coulomb force between the positively charged alpha particles and the atomic nuclei. This can be used to predict the expected number of alpha particles scattered at a particular angle (you do not need to know how to calculate this value in this course). By measuring the number of alpha particles scattered at a fixed angle as a function of energy we can determine the size of the nucleus. The experimental data given in figure 1.24 shows a deviation away from this model at about 25 MeV. This suggests another force is starting to effect the path of the alpha particles, this is the strong nuclear force and indicated the alpha particle is very close to the nucleus.
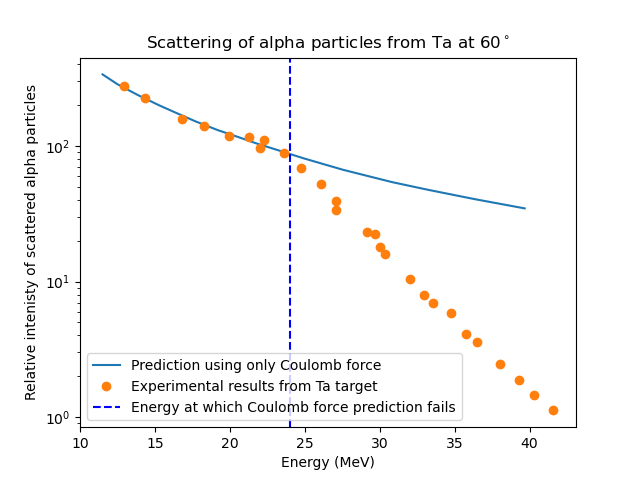
Fig. 1.24 The experimental data for alpha particles scattered from a Ta foil. At 25 MeV the prediction using only the Coulomb force fails. This indicates an additional force coming into play, in this case it is the strong nuclear force.#
If we neglect the scatting angle of 60\(^\circ\) and assume a head-on collision we can estimate the size of the nucleus by assuming all the kinetic energy of the alpha particle is used doing work against the electrostatic field of the atomic nucleus.
We now know the radius of the nucleus is about a Fermi (\(10^{-15}\)m), compared to the atomic radius of an Angstrom (\(10^{-10}\)m) this is very small.
