Fig. 2 illustrates the propagation of advanced and retarded waves. The advanced wave solutions of the electromagnetic wave equation are usually ignored as unphysical because they seem to have no counterpart in nature.
Go back to Table of Contents
Go back to Section 2.4
Continue to Section 3.3
3.0 The Transactional Interpretation of Quantum Mechanics
In the preceding chapter we applied the criteria of Section 1.1 to the Copenhagen interpretation as it deals with the interpretational problems of the quantum mechanical formalism. This exercise has shown that several interpretational problems are handled only superficially by the CI. The problem area is centered around CI4, the association of the state vector with subjective knowledge of the system by an observer. In this section we will present the transactional interpretation of quantum mechanics, an alternative to the Copenhagen interpretation which retains the CI's interpretational links between formalism and experiment but which replaces the subjectivity and the nonlocality evasions of CI4 with an objective and explicitly nonlocal description of quantum processes.
Our survey has illuminated several interpretational problems intrinsic in the CI. Based on this discussion, we can now define as goals a set of characteristics desirable in a more "ideal" interpretation: (1) It should permit the operation of the microcosm to be isolated from the macrocosm and particularly from intrinsically complicated macroscopic concepts, e.g., knowledge, intelligent observers, consciousness, irreversibility, and measurement; (2) it should account for the nonlocal correlations of the Bell inequality tests in a way consistent with relativity and causality; (3) it should account for the collapse of the state vector without subjective "collapse triggers" (e.g., consciousness); and (4) it should give added meaning to the state vector and provide insights into the problems of complexity, completeness, and predictivity.
With these goals in mind, we now present the transactional interpretation of quantum mechanics (TI). We will find that the TI, which is objective and explicitly nonlocal, satisfies each of these goals. It provides a description of the state vector as an actual wave physically present in real space. It provides a mechanism for the occurrence of nonlocal correlation effects through the use of advanced waves. The collapse of the state vector in the TI is the formation of a transaction which occurs by an exchange of retarded and advanced waves. The transaction model provides a way of clearly visualizing and developing intuition about the quantum phenomena which have remained mysterious and counter-intuitive for half a century.
3.1 Advanced Waves and Wheeler-Feynman Absorber Theory
The basic element of the transactional interpretation is an emitter-absorber transaction through the exchange of advanced and retarded waves, as first described by Wheeler and Feynman (1945, 1949) [see also (Feynman, 1967b)]. Advanced waves are solutions of the electromagnetic wave equation and other similar wave equations which contain only the second time derivative. Advanced waves have characteristic eigenvalues of negative energy and frequency, and they propagate in the negative time direction. Fig. 2 illustrates the propagation of advanced and retarded waves. The advanced wave solutions of the electromagnetic wave equation are usually ignored as unphysical because they seem to have no counterpart in nature.
The classical electrodynamics described by Wheeler and Feynman (WF) was intended to deal with the problem of the self-energy of the electron in an innovative way. Assuming the time symmetric formalism of Dirac (1938) combined with the ad hoc assumption that an electron does not interact with its own field, WF was able to formally eliminate the self-energy term from their electrodynamics. But along with self energy these assumptions also removed the well observed energy loss and recoil processes (i.e., radiative damping) arising from the interaction of the radiating electron with its own radiation field.
However, WF accounted for these well-known damping effects by allowing the emitting electron to interact with the advanced waves sent by other electrons which would ultimately, at some time future, absorb the retarded radiation. Thus the energy loss and recoil of the emitter were accounted for without having it interact with its own field. Moreover, the calculation succeeded in describing electrodynamic interactions in a completely time-symmetric way. To account for the observed asymmetric dominance of retarded radiation, WF invoked the action of external boundary conditions arising from thermodynamics. They thus avoided resort to the usual ad hoc "causality" condition usually needed to eliminate the advanced radiation solutions.
Regrettably, the WF paper, while mathematically correct, proved be an invalid way of dealing with self-energy. As Feynman (1949) later pointed out, the self-interaction is a necessary part of electrodynamics, needed, for example, to account for the Lamb shift. And it is relevant that the WF ad hoc assumption of non-interaction is not needed in their recoil calculations because, as later authors have pointed out (Pegg, 1975; Cramer, 1980), the electron cannot undergo energy loss or recoil, which are intrinsically time-unsymmetric processes, as a result of interacting with its own (or any other) time-symmetric field.
When the offending assumption of non-interaction is removed from the WF formalism, what remains is a classical self-consistent and time-symmetric electrodynamics which cannot be used to deal with the problem of self energy. Further, this WF formalism is not particularly useful as an alternative method of calculating the electrodynamics of radiative processes because the mathematical description of radiation explicitly involves the interaction of the emitter with the entire future universe. Thus a simple integration over local coordinates in the conventional formalism is replaced by an integral over all future space-time in the light cone of the emitter in the WF formalism.
However, this "difficulty" can be viewed an asset. The WF mathematics can be used to investigate the properties of cosmological models describing the future state of the universe by relating such models to radiative processes. In essence this approach provides a way of linking the cosmological arrow of time (the time direction in which the universe expands) to the electromagnetic arrow of time (the complete dominance of retarded over advanced radiation in all radiative processes). There is a considerable literature in this field which the author has reviewed in a previous publication (Cramer, 1983).
Although the original WF work dealt exclusively with classical electrodynamics, later authors (Hoyle and Narlikar, 1969, 1971; Davies 1970, 1971, 1972) have developed equivalent time-symmetric quantum-electrodynamic (QED) versions of the same approach. The predictions of these QED theories have been shown to be completely consistent with those predictions of conventional QED which can be compared with experimental observation {footnote 4}. It has also been shown (Davies, 1972) that despite this similarity of prediction, the time-symmetric QED provides a qualitatively different description of electromagnetic processes. It is essentially an action-at-a-distance theory with no extra degrees of freedom for the radiation fields and no second quantization. The field in effect becomes a mathematical convenience for describing action-at-a-distance processes.
There may also be another advantage to the WF approach to electrodynamics. Dirac's (1938) work on time-symmetric electrodynamics, on which the WF theory is based, was introduced as a way of dealing with singularities in the radiation field in the conventional theory near a radiating electron. Konopinski (1980) in his Lorentz covariant treatment of the radiating electron has pointed out that this time-symmetric "Lorentz-Dirac" approach eliminates such singularities and therefore amounts to a self-renormalizing theory. This formulation may have applications in eliminating related singularities in QCD and in quantum field theory in curved space-time.
3.2 The Emitter-Absorber Transaction Model
There is a second application of the Wheeler-Feynman approach which was introduced by the author in a previous publication (Cramer, 1980). The WF description of radiative processes can be applied to the microscopic exchange of a single quantum of energy, momentum, etc., between a present emitter and a single future absorber through the medium of a transaction, a Wheeler-Feynman exchange of advanced and retarded waves. 
Fig. 3 illustrates a simplified form (one space dimension and one time dimension) of the the transaction process.
The emitter, e.g., a vibrating electron or atom in an excited state, attempts to radiate by producing a field. This field, according to the Wheeler-Feynman description, is a time-symmetric combination of a retarded field which propagates into the future and an advanced field which propagates into the past. For simplicity let us first consider the net field to consist of a retarded plane wave of the form F1 ~ exp[i(k.r-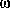
t)] for t
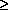T1 (T1 is the instant of emission) and an advanced plane wave of the form G1 ~ exp[-i(k.r- 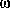t)] for t
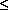T1. Since the retarded wave F1 has eigenvalues characteristic of positive energy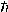 
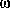and momentum 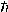k, while the advanced wave G1 has eigenvalues of negative energy -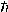 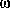and momentum - 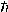k, the net loss of energy and momentum by the emitter in producing the pair of waves (F1 + G1) is zero, as might be expected from the time-symmetry of the composite wave.
Let us for the moment set aside consideration of the advanced wave G1 and follow the retarded wave F1. This wave will propagate in the positive time direction (t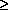T1) until it encounters an absorber. The process of absorption, as is well known, can be described as a movement of the absorbing electron (or atom) in response to the incident retarded field F1 in such a way as to gain energy, recoil, and produce a new retarded field F2=-F1 which exactly cancels the incident field F1. Thus the retarded wave from the absorber exactly cancels the retarded wave from the emitter, and there is no net field present after the instant of absorption T, i.e.:
Fnet = (F1 + F2) = 0 for t>T1. [3]
But the Dirac-Wheeler-Feynman assumption of time-symmetric radiative processes requires that the absorber can only produce the cancelling retarded field F1 for t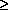T1 if it also produces an advanced field G2 for t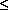T2. This field G2 will propagate in the negative time direction (i.e., into the past) from the instant of absorption T2, travelling back down the track of the incident wave F to the instant of emission T1. There it interacts with the radiating electron (or atom) at the instant of emission, causing it to recoil and to lose energy. Further, the advanced wave G2 continues to times such that t>T1, where it is superimposed on the advanced wave from the emitter G1 to produce a net advanced field:
Gnet = (G1 + G2). [4]
But the condition that F2=-F1 at the absorber for t<T2 brings with it a similar condition for the advanced fields, so that G2=-G1 at the emitter and for t<T1, so that Gnet=0 for t<T1. The result of the cancellation of the pre-emission and post-absorption waves is that only in the interval T1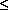t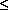T2 is there a non-zero field:
Fnet = (F1 + G2). [5]
From this we see that even under the Dirac assumption of time symmetric radiation of retarded and advanced waves the advanced field G1 cannot produce "advanced effects" such as backward-in-time signalling and the emission of negative energy radiation because it has been nullified by the absorption process.
This, in a simplified one-dimensional form which will be expanded below, is the emitter-absorber transaction. The emitter can be considered to produce an "offer" wave F1 which travels to the absorber. The absorber then returns a "confirmation" wave to the emitter and the transaction is completed with an "handshake" across space-time. To an observer who had not viewed the process in the pseudo-time sequence {footnote 14} employed in the above discussion, there is no radiation before T1 or after T2 but a wave travelling from emitter to absorber. This wave can be reinterpreted as a purely retarded wave because its advanced component G2, a negative energy wave travelling backwards in time from absorber to emitter, can be reinterpreted as a positive energy wave travelling forward in time from emitter to absorber, in one-to-one correspondence with the usual description {footnote 15}.
Thus the W-F time symmetric description of electrodynamic processes is completely equivalent in all observables to the conventional electrodynamic description. Time-symmetric electrodynamics, in both its classical and quantum mechanical forms, leads to predictions identical with those of conventional electrodynamics. For this reason it is not possible to devise experimental tests which will distinguish between time-symmetric and conventional electrodynamics. The intrinsic untestability of time symmetric electrodynamics reveals that it should be considered an alternative interpretation of the electrodynamic formalism rather than an alternative formulation.
It is this alternative interpretation of the electrodynamic formalism which we have generalized (Cramer, 1980) to include all quantum mechanical processes and which leads to the alternative interpretation of quantum mechanics which is presented here. The fundamental element of this interpretation is the emitter-absorber transaction, a simple plane-wave version of which was described above. The transaction is a "handshake" between the emitter and the absorber participants of a quantum event, occurring through the medium of an exchange of advanced and retarded waves. The description just presented is basically one dimensional (in space) and is not fully applicable to the case of three space dimensions with quantization boundary conditions. Before discussing the applications of the interpretation we will generalize the transaction model from one to three spatial dimensions.
There are two problems with the one dimensional plane wave description employed above: (1) it does not explicitly deal with the attenuation and modification of wave amplitude due to propagation through space or to passage through attenuating media; and (2) it does not explicitly include the quantum conditions on the transfer of energy, angular momentum, charge, etc., which are an important aspect of all quantum mechanical processes. In the case of quantum electrodynamics the photon energy quantization condition E=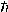 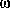places an extra constraint on the electromagnetic wave equation, requiring that an integer number of quanta be exchanged between emitter and absorber despite the action of intervening space, filters, mirrors, slits, wave plates, etc., in reducing or modifying the amplitudes of the advanced and retarded waves exchanged between emitter and absorber.
For this reason, the two-step pseudo-time sequence {footnote 14} of Fig. 3 and the associated plane wave description must be replaced by a multi-step sequence allowing for spherical and more complicated wave forms and which proceeds until all relevant quantum conditions are met. In particular, we must view the transaction as occurring in pseudo-sequential form which includes an "offer", a "confirmation" and a completed transaction.
Fig. 4 illustrates this more general form of transaction. In the first pseudo-sequential step (1) the emitter located at (R1,T1), sends out a waves F1(r,t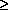T1) and G1(r,t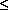T ) (which can be of spherical or more complicated form) in all possible spatial directions. In step (2) the absorber located at (R2,T2), receives the attenuated retarded wave front F1(R2,T2) and is stimulated to produce a response wave G2(r,t) which has an initial amplitude proportional to the local amplitude of the incident wave which stimulated it:
G2(r,t) ~ F1(R2,T2)×g2(r,t) [6]
Here g2(r,t) is a unit advanced wave, i.e., the advanced equivalent of the retarded wave F1(r,t) in that g2(r,t-T2)=[F1(r,t-T1)]*.
In step (3) the advanced wave G2 propagates back to the locus of emission, at which it has an amplitude which is proportional to its initial amplitude F1(R2,T2) multiplied by the the attenuation which it has received in propagating from the absorption locus to the emission locus. But the advanced wave G2 travels across the same spatial interval and through the same attenuating media encountered by F1, but in reverse. For this reason, the unit amplitude wave g2(R1,T1) arriving back at the emitter has an amplitude which is proportional to F1*(R2,T2), the time reverse of the retarded wave which reached the absorber. Thus at the emission locus the advanced wave amplitude G2 is:
G2(R1,T1) ~ F1(R2,T2) ×F1*(R2,T2) = |F1(R2,T2)|2. [7]
This means that the advanced "confirmation" or "echo" wave which the emitter receives from the absorber as the first exchange step of the incipient transaction is just the absolute square of the initial "offer" wave, as evaluated at the absorber locus. The significance of this 
* echo and its relation to Born's probability law will be discussed in Section 3.8 below.
In step (4) the emitter responds to the "echo" and the cycle repeats until the response of the emitter and absorber is sufficient to satisfy all of the quantum boundary conditions [E=h(nu) and various conservation laws], at which point the transaction is completed. Even if many such echoes return to the emitter from potential absorbers, the quantum boundary conditions can usually permit only a single transaction to form. The transaction formation can be considered as analogous to the establishment of a four-vector standing wave across the interval bounded by (R1,T1) and (R2,T2), the two loci forming terminating "walls" outside which the wave amplitude must make no contribution to the process. Note that at the completion of step (4) the local fields in the vicinity of both the emitter and the absorber are real (as opposed to complex) because they are a superposition of an advanced and a retarded wave of equal amplitude and the same phase. The significance of this for the problem of complexity is discussed in Section 3.6 below.
To summarize the transaction model, the emitter produces a retarded offer wave (OW) which travels to the absorber, causing the absorber to produce an advanced confirmation wave (CW) which travels back down the track of the OW to the emitter. There the amplitude is CW1~|OW2|2, where CW1 is evaluated at the emitter locus and OW2 is evaluated at the absorber locus. The exchange then cyclically repeats until the net exchange of energy and other conserved quantities satisfies the quantum boundary conditions of the system, at which point the transaction is complete. Of course the pseudo-time sequence {footnote 14} of the above discussion is only a semantic convenience for describing the onset of the transaction. An observer, as in the simpler plane wave case, would perceive only the completed transaction which he could reinterpret at the passage of a single retarded (i.e., positive energy) photon travelling at the speed of light from emitter to absorber {footnote 15}.
But an equally valid interpretation of the process is that a four-vector standing wave has been established between emitter and absorber. As a familiar 3-space standing wave is a superposition of waves travelling to the right and left, this four-vector standing wave is the superposition of advanced and retarded components. It has been established between the terminating boundaries of the emitter, which blocks passage of the advanced wave further down the time stream, and the absorber, which blocks passage of the retarded wave further up the time stream. This space-time standing wave is the transaction, and which we will it use as a basis for the discussion which follows.
It should be emphasized that the TI is an interpretation of the existing formalism of quantum mechanics rather than a new theory or revision of the quantum mechanical formalism. As such, it makes no predictions which differ from those of conventional quantum mechanics. It is not testable except on the basis of its value in dealing with interpretational problems. The author has found it to be more useful as a guide for deciding which quantum mechanical calculations to perform than to the performance of such calculations. As will be demonstrated in Chapter 4, the main utility of the TI is as a conceptual model which provides the user with a way of clearly visualizing complicated quantum processes and of quickly analyzing seemingly "paradoxical" situations (e.g., Wheeler's delayed choice experiments, Herbert's paradox, the Hanbury-Brown-Twiss effect, and the Albert-Aharonov-D'Amato prediction) which would otherwise require elaborate mathematical analysis. It is a way of thinking rather than a way of calculating. It may have value as a pedagogical tool for the teaching of quantum mechanics to students. It also seems to have considerable value in the development of intuitions and insights into quantum phenomena that up to now have remained mysterious.
Continue to Section 3.3
Go back to Section 2.4
Go back to Table of Contents