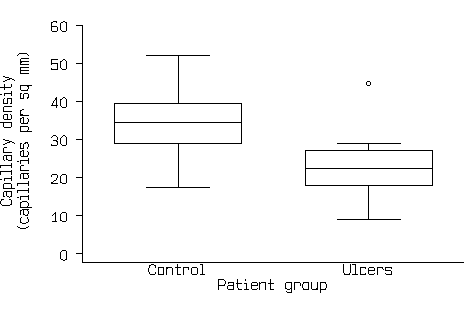I had very few comments on specifically on presentation in my Lancet reviews, although my Allstat respondents had quite a lot to say. I made a suggestion that the zero should be included on the y-axis of a graph, and I made this point about a graph:
`I think a scatter plot, showing the actual data, would be much more informative. Are the thin lines standard errors?'
On similar lines, one of my Allstat respondents complained about:
'Dynamite pushers, skyscrapers with TV-aerials'.
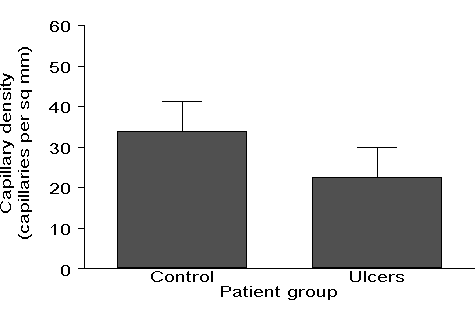
What he had in mind, and on which I had been commenting, was a graph like Figure 1:
Figure 1. Bar graph showing capillary density (per mm2) in the feet of ulcerated patients and a healthy control group (data, but not graph, supplied by Marc Lamah).
You see graphs like this frequently in journals and it may come as a surprise to researchers that many statisticians dislike them intensely. There are several reasons for this. My Allstat respondents complained about:
'Summary graphs with less information than the original data.'
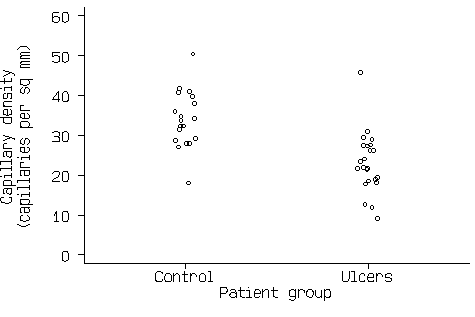
Figure 2. Scatter graph of the capillary density data.
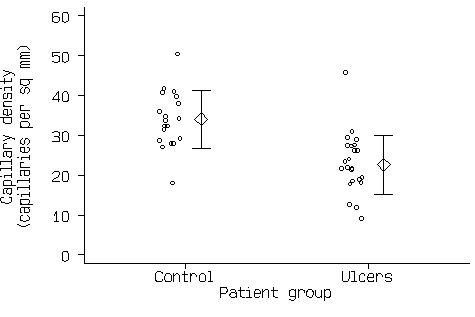
Figure 3. Scatter graph of the capillary density data with mean and standard deviation added.
This now shows all the information in Figure1 and Figure 2. If there are a large number of points, the scatter diagram will become a mass of indistinguishable points. In this case we can use box and whisker plots (see Bland 2000a), as in Figure 4.
Figure 4. Box and whisker graph of the capillary density data.
These do not give all the information in a scatter diagram, but they do show central tendency, spread and the shape of the distribution. We can see from Figure 4 that the distributions are roughly symmetrical, apart from one rather extreme point, that the control group tend to have higher capillary density that the ulcer group, and that the data are suitable for the t distribution to be applied.
My Allstat respondents had quite a lot to say. A common complaint about graphs such as Figure 1, which I had made in my review, is that authors do not always make clear what the vertical lines represent, standard deviations, standard errors, or confidence intervals, an irritation which I mentioned above concerning '±' notation. A third objection to the bar graph shown in Figure 1 is that it has only four numbers in it, which could be reported much more efficiently in the text. Two of my respondents made similar points:
'Using bar charts to show that the proportion of women in the study was 55% and men 45%, and similar low information ways of using ink and space.' (Two similar replies.)
On the other hand, one respondent complained about:
'Tables of data with (literally) hundreds of figures when the information content is minimal and a graph would be more useful.'
The Lancet instructs its authors to 'Use graphs as an alternative to tables with many entries'. Personally, I am usually inclined to tables rather than graphs. I think that this bias (yes, I have them!) arises because I do not have a strong visual imagination or ability to think pictorially. However, I also think that the argument that other researchers can make use of your findings more easily if they are presented numerically rather than graphically is a forceful one, and this should lead us to choose numbers when in doubt.
I have no problems with the view of my respondents who were irritated by authors:
'Giving far too many decimal places.' (3 replies).
The week before writing this, I reviewed a paper which gave all P values, F statistics, and even degrees of freedom to four decimal places, e.g. 'F=1.9367 with 34.3452 and 45.3298 degrees of freedom, P=0.0189'. This used an approximation to the F distribution which involved changing the degrees of freedom, making them fractional. Now I doubt that the F statistic conveys much useful information anyway, but all those decimal places do not. There is no point in reporting F, t, or chi-squared statistics to more than two decimal places. I do not think that anything would be lost by reducing the decimal places to two here: 'F=1.94 with 34.35 and 45.33 degrees of freedom, P=0.019'. Indeed, I would render the P value to one significant figure: 'P=0.02'. Only the first non-zero number and the number of zeros preceding it are important. The reason for this profligate and unconsidered reporting of many decimal places must be that computer programs deliver them. Programmers try to give the users everything they could possibly want and if the program calculates the F statistic to seven significant figures, why not print them out? But this is no reason for the researcher to burden his readers with them. They often make text and tables much more difficult to read. Correlation coefficients are frequent example. Programs often print them to four decimal places, but is there really any important difference between 'r=0.3421 and 'r=0.3379'? I think that 'r=0.34' would do very nicely for both and make the meaning text and tables easier to grasp.
One respondent complained about something which I also dislike:
'Using multiple crosshatched three-dimensional bars' (2 replies).
I find that three-dimensional effects seldom make a graph clearer. The effect is usually to make it more difficult to read.
Assumptions
Many statistical methods require the data to meet some assumptions, such as that data follow a Normal distribution with uniform variance. Such assumptions are often not checked, particularly for t methods. The statistical referee can often detect skewness from the data and graphs given in the paper (Altman and Bland 1996). One giveaway is a standard deviation which is greater than half the mean, which implies that two standard deviations below the mean would be a negative number. For most measurements negative values are impossible we could not have any observations less than mean minus two standard deviations, and 2.5% of observations from a Normal distribution would be found there. Such data cannot therefore be from a Normal distribution. Another is to give mean or median and quartiles or extreme values. If the mean or median is not close to the centre of the interval determined by the limits, we should suspect that the distribution is skew. Yet another betrayer of non-Normal distributions can arise when the mean and standard deviation or standard error are calculated separately for several different groups, then given in a table or graph. The standard deviation should not be related to the mean. Often we see that groups with large means also have large standard deviations. A scatter diagram of the data, while highly desirable, can also reveal deviations from the assumptions of statistical methods. I three examples of obvious deviations from assumptions in my 15 papers:
`Are the thin lines standard errors? If so, they suggest that the data are not Normal, which casts doubt on the F test.'
`I would be surprised if these measurements followed Normal distributions. Figure 2 suggests that this is not the case, as the distribution of X looks positively skew. The authors should check the distributions of their variables, and use a logarithmic transformation where appropriate.'
`The data are very skewed, positively for X (mean 17.6, range 16.0-21.7) and negatively for Y (mean 8.6, range 4.9-9.4). This is produced by the selection criteria for the trial, which accepts subjects with X > 16.0 and Y < 9.5. No attempt is made to allow for this in the analyses, which assume that data follow Normal distributions.'
To my surprise, only one of my respondents mentioned this:
'Authors who don't attempt to check the normality of their data and use normal theory with clearly non-normal data.'
Incorrect descriptions of statistical methods
The Lancet specifies that authors should: 'Put a general description of methods in the Methods section. When data are summarized in the Results section, specify the statistical methods used to analyze them.' This is good advice. It is certainly annoying when authors do not tell the reader what statistical method is being used and I had an instance in my 15 reviews, in one of which I complained that:
`The statistical test used should be stated.'
My Allstat respondents thought this was an important problem, complaining about:
'Authors who assume that the description of the statistics is so unimportant that they don't actually give any information at all' (5 similar replies).
One had a specific complaint about authors:
'Stating only that "statistical analysis was done using x computer package"'.
Telling us which package was used is important, as they are not all the same and many statistical methods can be implemented in different ways which may give different answers. Indeed, the Lancet asks for it: 'Specify any general-use computer programs used'. But it is not enough to tell us what is being done. In mathematical language, we would say that it is necessary but not sufficient. This reported statistical methods section deserves to become a classic of pointless minimalism:
'The analysis was performed on an IBM486, under MSDOS'
A less frequent, but also irritating, practice is not using the methods stated in the method section of the paper. It is easy to do this, as papers often go through many drafts, with parts being cut out and new one inserted, but it is annoying when an obscure method is references and the referee spends time looking it up only to find that this time had been wasted. I had an example of this in my 15 papers:
`I do not think Hotelling's t test is actually used anywhere.'
An Allstat respondent made the same point:
'Reference in the methods section to analyses undertaken but with no results appearing anywhere in the report.'
This comment from my reviews combined a method reported in the method section which was not used with not saying what done in the analyses which were reported:
`I think that tests other than paired t tests were done. I can't actually find any data suitable for a paired t test. ... the appropriate method would be Fisher's exact test, which gives P=0.2 ... this should be a rank correlation. I get tau=0.37, P=0.08 . . . The appropriate method would be Fisher's exact test, which gives P=0.09.'
I have no idea what they had actually done, but I was pretty confident that whatever it was, was wrong. Sometimes I had to pinch myself to reassure myself that this was not a ghastly nightmare, and that people had really submitted to this stuff to the world's most prestigious medical journal.
Baseline characteristics in randomised trials
Baseline characteristics deserve special mention because two common parastatisical practices relate to them. Baseline characteristics are those which we record after subjects have been recruited to the trial but before treatment begins. There are several good reasons for making and reporting baseline measurements. The first of these is obvious: we want to describe the population which our trial subjects represent. The second is that we want to check and demonstrate that the randomization process has worked. This is not always the case. I was asked to advise on a trial where a programming error had resulted in almost all the older subjects being allocated to one arm of the trial a nd almost all the younger subjects to the other. My advice had to be 'Do it again'. (MacArthur 2001) The third is that we may want to adjust the treatment difference for prognostic variables. If a variable measured at baseline is a strong predictor of the outcome of treatment, adjusting for it statistically may lead to reveal treatment effects which were masked. Altman (1991) gives a good example.
The first common parastatistical mistake is to carry out tests of significance on the baseline variables between the randomized treatment groups. Randomization produces treatment groups which are random samples from the same population. Therefore, any null hypothesis that states that there is no difference between the populations from which the groups come is true. Any significant differences between the treatment groups have arisen by chance; they are type I errors. I had two examples of this in my 15 reviews:
`The tests of significance at baseline should not be done. If the subjects are randomized, they come from the same population and the null hypothesis is true. There is no reason to test it.'
`There is no need to test the difference between the groups before the withdrawal of treatment. Because they are randomised, they are from the same population until treatment is changed, and hence the null hypotheses are true.'
One of my Allstat respondents mentioned this, too, complaining about:
'Significance testing of baseline variables in RCTs.'
The second parastatistical error is that, having tested for differences between baseline characteristics, adjustment of the difference in the outcome measurement between treatments is done for those variables which are significant one the baseline measurements but not for any others. It is not the chance relationship of baseline variables to treatment which is important, but their relationship to the outcome variable. Even when the treatment groups are exactly balanced for the prognostic variable, adjusting for it statistically should remove a lot of variability from the error term and so make confidence intervals narrower and possibly make P values smaller. I had a good example of this approach in one of my reviews:
`The statement that adjustment for baseline characteristics is not needed because baseline differences are not significant is quite wrong. Such adjustments may reduce the variability and so improve the power.'
An Allstat respondent made the same point, complaining about authors:
'Not reporting analyses adjusted for baseline values of prognostic covariates.'
A miscellany
A lot of other issues came up once or twice, either in my own reviews or from my correspondents. I think that this represents the tip of a very large iceberg of possible mistakes on the part of researchers. I present them in the hope that my readers will in future avoid these particular ones at any rate.
An occasional mistake is to include repeated measurements on same subject as if they were different subjects. The data are then analysed using methods which assume that the observations are independent. This can have the effect of making P values too small and confidence intervals too wide. I had a couple of examples in my reviews:
`It is wrong to mix multiple observations from different subjects in this way (Bland and Altman 1994). An appropriate method is described by Bland and Altman (1995).'
`It is not clear why two subjects were measured twice. Inspection of Table 1 suggests that the intention was to measure at 18 hours but that subject 3 was tested additionally at 2 hours and subject 5 at 48 hours. This should be clarified. Repeat observations on the same subject and observations on different subjects cannot be mixed as if they were all independent. I suggest that the first observation on subject 3 and the second on subject 5 should be omitted from the statistical analysis, as they are at very different times.'
The same problem can occur on a larger scale:
`However, they ignore the fact that these 21 groups of subjects are from 9 different trials, and analyse the data as if they are all from the same population.'
Again, this would have the effect of making the P values too small and the confidence intervals too wide. There are well-established mbethods of meta-analysis (see, for example, Bland 2000b) for carrying out the combination of data from different trials and authors should use them.
Significance test methods based on rank order, such as the Mann Whitney and Wilcox on tests and those associated with the Spearman and Kendall rank correlation coefficients, are inappropriate when samples are very small. One cannot have a significant two-sided test at the 5% level when samples are smaller than two groups of four for the Mann Whitney U test or less than six for the Wilcoxon paired test or the rank correlation coefficients. Each possible rank ordering has probability greater than 0.05. Hence rank methods on very small samples are inevitably not significant and there is no point in using them. I made this point in one of my reviews:
`Rank methods are inappropriate for such small samples as they cannot detect any differences, no matter how large the difference is.'
Curiously, I have been asked by publishers to review at least three proposals for introductory statistics text-books (not written by statisticians) which contained the statement that when we have fewer than six observations we should use non-parametric methods, because parametric methods such as t tests are inappropriate, it being impossible to verify the Normal distribution assumptions. The opposite is the case, because parametric methods can produce significant differences for very small samples although rank-based methods cannot. I wish I knew the source of this often-repeated idea. As for checking the Normal assumption, we often have a good idea from other data whether this is reasonable.
Correlation coefficients can cause a problem because there is an assumption that the same is a representative (i.e. random) sample of its population and that both variables are random variables. They should not be used when the values of one variable are set by the experimenter. I had two instances of this in my reviews:
` . . . Correlation is inappropriate when one of the variables is fixed by the investigator (dose and time) . . . One and two sample t methods and regression should be used.'
`The statement that there is no significant correlation between time of measurement and X is meaningless. The times are almost equal except for the duplicate measurements. The ratio is much higher for the early measurement and much lower for the late measurement, suggesting that there is a possibility of a strong relationship with time.'
One my respondents, somewhat enigmatically, cited:
'Spurious use of correlation and regression (oh dear not again!)'
Statisticians mostly have a background in mathematics, as do I, and have been trained for many years to think logically. Indeed, a colleague, Shirley Beresford, once remarked that she thought that the main contribution of statisticians in medical research was not to carry out statistical analyses but 'to inject a bit of logic into the situation'. So imbued with logic are we that we can forget that this is not the only way of thinking and is not the main method of thinking for most people, nor is it always the most useful. Thus to us this one is jaw-dropping:
`The comparisons of X means between the low X and high X groups are not useful. If we divide subjects according X and then compared the mean X between the two groups, of course it will be significant. We could do the same thing with their telephone numbers.'
Of course, the null hypothesis that a group chosen to have X below a cut-off and a group chosen to have X above the cut-off the mean X will be the same is inevitably false. As we know this, there is no point in testing it. I presume the authors simply split the subjects into two groups then tested everything between them. One of my Allstat respondents made a similar point about:
'Dichotomising continuous variables especially if they identify 'responders' and 'non-responders' using these variables.'
Splitting the subjects into two groups using a continuous variable reduces the amount of information which we have. P values may become larger and we may miss important relationships. Some researchers might be tempted to split the sample not at an arbitrary cut-off, such as the overall mean, but to choose a cut-off to minimise a P value and make a relationship significant. This is a real misuse of statistics and will produce misleading results.
The authors of one of the Lancet papers were particularly unlucky (or lucky, depending how you look at it) because they were applying my own work on agreement between methods of measurement and received this comment:
'I suggest replacing the term "95% confidence intervals of agreement" by "95% limits of agreement". The "95% limits of agreement" of Bland and Altman are not a confidence interval, but two point estimates.'
My Allstat respondents came up with a lot more. One mentioned:
'Chi-square test analyses of ordered categorical data.'
What was meant is that we often have categorical data where the categories are ordered in some way, such as physical condition being classified as 'poor', 'fair', 'good' or 'excellent'. The usual chi-squared test for a contingency table ignores this ordering and tests the null hypothesis of no relationship of any sort between the variables. (NEED REAL EXAMPLE HERE.) This is usually a mistake, but an understandable one. Many textbooks use examples with ordered categories to illustrate chi-squared tests.
Another gave the example of
'Rate per 1000 person-years = 3 (95% CI -3 to 9).'
The rate of something per year cannot be negative, so the calculation of the confidence interval has produced an impossible lower limit. This happens because researchers use methods designed for the analysis of large samples or large numbers of events to small samples or small numbers of events. They calculate standard errors and then calculate the confidence interval using the Normal distribution, as the observed value ± 1.96 standard errors. But if the number of events or the sample size is not large enough for this Normal approximation we can get negative lower limits. The same thing can happen with proportions close to the top of their range of possible values, such as sensitivities and specificities, which are sometimes given confidence intervals with upper limits above 100%. There are better approximations and exact methods which can be used in these cases to give confidence intervals which do not include impossible values. Even zero would be an impossible lower limit for the rate in the example, for if in the sample we had observed a case, as we must to get a rate of 3 per 1000 person-years, then the rate in the population cannot be zero. We sometimes see confidence intervals like the one given presented as '3 (95% CI 0 to 9).' This happens because researchers calculate the interval as -3 to 9, recognise that -3 is impossible, and replace it with zero.
My respondents made a couple of general points about the way statistics is carried out in medical research. One complained about:
'Papers where the statistical methods are copied from a previous paper in the field, which was in turn copied from a previous paper, which was in turn . . .'
This undoubtedly happens, and most statisticians have had the experience of researchers who say that a published paper had used a particular method of which the statistician disapproves, and was published, so why shouldn't they? Another respondent complained about:
'Doctors who don't realise that statistics is an advancing science; and the best methods of 20 years ago are not always the best methods of today.'
Well, I think that there are plenty of statisticians in this category, too, and I have no doubt that I am guilty of this from time to time. I do not think we can expect researchers to keep up with what is happening in statistics as well as in their own field. Perhaps, though, we can expect them to embrace a new and better technique when the referee has pointed it out.
One despondent respondent commented:
'There is no hope, at times.'
Not taking us seriously
Some of my respondents complained about authors' attitude to statisticians: These included:
'Papers which show no sign of having had input from a statistician.'
I can sympathise with this, but statisticians can be hard to find for many researchers. The trouble is, you don't know what you don't know, so it hard to spot your own mistakes or to realise that you need help. I think that it should be much easier for researchers to get not just statistical advice but also collaboration. Trying to teach doctors how to analyse their own data is very inefficient. It requires a different way of thinking from medicine, and few people can do both. It is much better to train statisticians to collaborate with them. An additional advantage, unfortunately, is that we do not pay the statistician as much as the doctor, so it makes economic sense too. Another respondent felt that statisticians did not get the prominence they deserved:
'Acknowledgements to a statistician who clearly did all the analysis and should be on the paper.'
Researchers sometimes ask me whether I would like to be acknowledged for my help. I usually paraphrase Oscar Wilde and tell them that there is only one thing worse than being acknowledged, and that is not being acknowledged. I think that the role of the statistician in research is often worthy of authorship, but when I think I am entitled to be an author I am usually welcomed. I think that statisticians have to make clear to researchers who consult them that they have to have something to show for the time they spend in advisory work and that if they make a real contribution, they should be included in the author list. On the other hand, I often refuse authorship because I feel that I have not done enough or could defend the paper.
Two respondents commented on the attitude of authors to statistical referees:
'People who ignore referees comments and send [the] paper to another journal.'
Sometimes this is all an author can do, but I agree that usually authors should take note of what referees say. If, as can happen, the referee has missed the point of the paper entirely, the author should ask why and see how the point can be clarified. Another respondent mentioned:
'The view of many doctors that any comment made by a statistician regarding the quality of the design must by definition be niggling and unimportant.'
I have been accused of being an academic who does not understand the real world of life and death in which doctors operate. This may be true, but so what? I understand something about the world of research and its interpretation. On the whole though, I get on very well with medical profession and have found them warmly welcoming.
The author bites back
Some respondents did not answer my question about what researchers did to annoy referees, but got a few things off their chests about what reviewers did to annoy authors. One complained about:
'Making comments which you know are a matter of opinion and not fact without declaring them as such.'
This is fair enough. If a referee knows that something is only a matter of opinion, they should not condemn others for disagreeing. Another complained about referees:
'Suggesting extensions to analyses which you know will involve far more work than is justified by any likely improvement to the analysis.'
If a referee did really know this then complaints would be justified. Another respondent did not like referees:
'Taking far more time to review a manuscript than is reasonable.'
Mea culpa to that. Refereeing is a difficult task for which one gets little or know reward and which competes for time with the work for which the statistician is paid. Some journal do pay a small fee, but it could not possibly compensate for the time spent in understanding a paper and finding the holes in it. However, I will try to do better.
'Using the anonymity usually afforded to pursue your own interests.'
My own experience as a statistical referee is that I am not remotely interested in the papers which I sent and I am not clear how I could pursue my own interests by impeding their publication. This is more likely to be a complaint about specialist referees who are working in the same area.
'I am giving a pet hate of my own about statistical referees. It is the apparently absolute conviction that their own method of dealing with a data set, whether it be by confidence intervals for differences between groups, their favourite (and usually obscure) measure of agreement, or idiosyncratic ways of normalising data before analysis, is the only right and proper one. In fact, as we all know, a collection of statisticians represents a variance of at least two standard deviations, and they agree to an even lesser extent than psychiatrists. So let's have a bit more humility, please.'
I wondered if the comment about the measure of agreement was a dig at myself. I am quite keen on confidence intervals for differences, too. However, it is certainly true that there is often more than one acceptable way to analyse data. I am irritated by referees who always insist on nonparametric methods because they do not believe that any data follow a Normal distribution, and by those who always insist that nonparametric methods are replaced by parametric ones.
What really upsets me
When I first gave this talk, without the Allstat sample, one of my audience said that he did not think that any of the things I had mentioned really upset me. He thought that what really annoyed me was statistics not being taken seriously by researchers.
I did not think this was the case. I think that what really upset me about this refereeing experience was that there were so many errors in so few papers, and in papers submitted to one of the world's most prestigious medical journals. The journal's own guidelines were ignored. Nothing about most of these papers suggested that the authors had read them.
This suggests a lack of care about research, regarding it as an unimportant activity which does not merit the effort which one hopes these medical researchers put into other aspects of their work. This matters. Incorrect analysis may lead to incorrect conclusions. Incorrect conclusions may lead to incorrect treatments and advice to patients. People can die.
How to avoid upsetting the statistical referee
We can draw a few tentative conclusions from this study. The things which should be avoided above all are:
- Read the journal's instructions to authors. If they do not cover statistics, use those of one of the major general medical journals.
- Never, ever, conclude that there is no difference or relationship because it is not significant.
- Give confidence intervals where you can.
- Give exact P values where possible, not P<0.05 or P=NS, though only one significant figure is necessary.
- Be clear what your main hypothesis and outcome variable are. Avoid multiple testing.
- Get the design right, be clear about blinding and randomisation, do a sample size calculation if you can.
- Be clear whether you are quoting standard deviations or standard errors, avoid '±' notation.
- Avoid bar charts with error bars.
- Check the assumptions of your statistical methods.
- Give clear descriptions of your statistical methods.
- Decide for which baseline characteristics you should adjust in advance, then do it.
A good aid to writing up clinical trials, and worth reading anyway, is the CONSORT statement (Moher et al., 2001), a template for doing this developed by a group of statisticians and trialists. If you follow this you should sail through the refereeing process.
And finally
I'll finish this talk with three comments from my Lancet reviews:
`The statistics are all wrong but it should be fairly easy to put them right. What a huge number of authors and none of them understand statistics!'
`Why do they do a totally statistical project without a statistician? I suggest they get one!'
And just to show that not all my 15 reviews were negative:
`My comments are very minor, not enough to make me rate any part of the paper as inadequate. I like it.'
Acknowledgements
I thank Donald Singer for first suggesting the topic, the editors of the Lancet for providing such rich source material, and my Allstat respondents, including Colin Chalmers, Rick Chappell, Tim Cole, Margaret Corbett, Carole Cull, Keith Dear, Michael Dewey, Simon Dunkley, the late Nicola Dollimore, Clarke Harris, Dan Heitjan, Jim Hodges, Alan Kelly, Peter Lewis, Russell Localio, Alison Macfarlane, Sarah MacFarlane, David Mauger, Richard Morris, Ian Plewis, Mike Procter, Paul Seed, Stephen Senn, Jim Slattery, Anthony Staines, Graham Upton, Andy Vail, Ian White, Sheila Williams, Ian Wilson, and a few whose names did not come through with the email.
References
Altman, D.G. (1991) Practical Statistics for Medical Research Chapman and Hall, London, p. 389-391. Back to text.
Altman DG, Bland JM. (1996) Detecting skewness from summary information. British Medical Journal 313, 1200. Back to text.
Altman DG and Bland JM. (2003) Interaction revisited: the difference between two estimates. 326, 219. Back to text.
Altman DG, Matthews JNS. (1996) Interaction 1: Heterogeneity of effects. British Medical Journal 313, 486. Back to text.
Bland JM, Altman DG. (1994) Correlation, regression and repeated data. British Medical Journal 308, 896. Back to text.
Bland JM, Altman DG. (1995) Calculating correlation coefficients with repeated observations: Part 1, correlation within subjects. British Medical Journal 310, 446. Back to text.
Bland M (2000a) An Introduction to Medical Statistics, 3rd edition Oxford, University Press. Section 4.5 Medians and quantiles. Back to text.
Bland M (2000b) An Introduction to Medical Statistics, 3rd edition Oxford, University Press. Section 17.11 Meta-analysis: data from several studies. Back to text.
Chalmers I. (1999) Why transition from alternation to randomisation in clinical trials was made. British Medical Journal 319, 1372. Back to text.
Gardner, M.J. and Altman, D.G. (1986) Confidence intervals rather than P values: estimation rather than hypothesis testing. British Medical Journal 292, 746-50. Back to text.
MacArthur C, Shennan AH, May A, Whyte J, Hickman N, Cooper G, Bick D, Crewe L, Garston H, Gold L, Lancashire R, Lewis M, Moore P, Wilson M, Bharmal S, Elton C, Halligan A, Hussain W, Patterson M, Squire P, de Swiet M. (2001) Effect of low-dose mobile versus traditional epidural techniques on mode of delivery: a randomised controlled trial. Lancet 358, 19-23. Back to text.
Matthews, D.E. and Farewell, V. (1988) Using and understanding medical statistics, second edition Karger, Basel, Back to text..
Matthews JNS, Altman DG. (1996a) Interaction 2: compare effect sizes not P values. British Medical Journal 313, 808. Back to text.
Matthews JNS, Altman DG. (1996b) Interaction 3: How to examine heterogeneity. British Medical Journal 313, 862. Back to text.
Moher D, Schultz KF, Altman DG. (2001) The CONSORT statement: revised recommendations for improving the quality of reports of parallel group randomized trials. Lancet 357, 1191-1194. Back to text.
Newnham, J.P., Evans, S.F., Con, A.M., Stanley, F.J., Landau, L.I. (1993) Effects of frequent ultrasound during pregnancy: a randomized controlled trial. Lancet 342, 887-91. Back to text.
Schulz, K.F., Chalmers. I., Hayes, R.J., and Altman, D.G. (1995)
Bias due to non-concealment of randomization and non-double-blinding.
Journal of the American Medical Association 273, 408-12.
Back to text.
Appendix
From the Lancet's instructions to authors:
Statistics
Describe statistical methods with enough detail to enable a knowledgeable reader with access to the original data to verify the reported results. When possible, quantify findings and present them with appropriate indicators of measurement error or uncertainty (such as confidence intervals). Avoid relying solely on statistical hypothesis testing, such as the use of P values, which fails to convey important quantitative information. Discuss the eligibility of experimental subjects. Give details about randomization. Describe the methods for and success of any blinding of observations. Report complications of treatment. Give numbers of observations. Report losses to observation (such as dropouts from a clinical trial). References for the design of the study and statistical methods should be to standard works when possible (with pages stated) rather than to papers in which the designs or methods were originally reported. Specify any general-use computer programs used.
Put a general description of methods in the Methods section. When data are summarized in the Results section, specify the statistical methods used to analyze them. Restrict tables and figures to those needed to explain the argument of the paper and to assess its support. Use graphs as an alternative to tables with many entries; do not duplicate data in graphs and tables. Avoid nontechnical uses of technical terms in statistics, such as "random" (which implies a randomizing device), "normal," "significant," "correlations," and "sample." Define statistical terms, abbreviations, and most symbols.
The Lancet's full instructions to authors are well worth reading.
Back to Some full length papers and talks.
Back to Martin Bland's Home Page.
This page is maintained by Martin Bland.
Last updated: 19 August, 2004.