1.5. Wave properties of particles

1.5.1. The de Broglie relation

A change of career

Maurice de Broglie, the brother of Louis de Broglie, was an early believer in Compton’s interpretation of the particle nature of light. The work impressed his brother Louis so much that he changed career from studying history to physics. In his PhD defence (1924) Louis de Broglie propose that particle may posses wave properties, five year later he was rewarded with a Nobel Prize.

Louis de Broglie proposed (often called the de Broglie hypothesis) that the particle like properties of waves should also apply in reverse, i.e. that particles should have wave like properties. Just as photons have wave properties that govern their motion, particles also have wave properties which we will show govern their motion. We will refer to this phenomena as wave-particle duality. The wave nature of particles that lead to come of the most interesting observations. The de Broglie relationship is written mathematically as

(1.11)\[ \lambda=\frac{h}{p} \]

where \(\lambda\) is called the de Broglie wavelength, \(h\) is Planck’s constant, and \(p\) is the momentum of the particle.

1.5.2. Electron diffraction: The Davisson-Germer experiment

The wave properties of electromagnetic (EM) radiation only be become evident when the dimensions of the experiment are comparable to the wavelength of the EM radiation. Hence, it is diffraction experiments, where waves are passed through an aperture comparable to the wavelength, that easily show us the wave nature of EM radiation. The wave nature of particles will be observed under similar conditions. What is the wavelength of an electron with 54 eV kinetic energy?

\[ \lambda = \frac{h}{p} = \frac{h}{\sqrt{2mK}} = \frac{4.14\times 10^{-15} (eV\cdot s)}{\sqrt{2\times 511 \times 10^{3} (eV/c^2) \times 54 (eV)}} = 0.165 \text{ nm} \]

Don’t forget to account for the \(c^2\) is the units of mass when calculating your solution. We will take \(10^{-10}\)m as a typical wavelength of an electron, of course we can change this wavelength by increasing or decreasing the kinetic energy but the value is convenient as we know X-rays with a similar wavelength are diffracted by crystal structures. In order to observe diffraction we will need to diffract electrons from a regular crystal lattice which contains atoms spaced at an interval similar to this wavelength. This experiment was first performed by Davisson and Germer by scattering electrons from a Nickel target. A schematic representation of the equipment used is given in figure 1.13.

Fig. 1.13 A schematic of the Davisson and Germer experiment. Electrons from the filament on the left are accelerated by a potential difference that can be adjusted to control the kinetic energy and hence the de Broglie wavelength of the electrons. The electrons are scattered from a Nickel target and a movable detector records the current at a fixed scattering angle which we will refer to as \(\theta_\text{S}\).

In the experiment electrons are accelerated through a potential difference of \(V\) and gain kinetic energy \(qV\) where \(q\) is the electron charge, i.e. 100 V potential will accelerate electrons to 100 eV. The electron current after the electrons are scattered from a Nickel target is recorded by a movable detector. In the experiment performed by Davisson and Germer a potential difference of 54 V resulted in a maximum value of the electron current when the detector was at 50\(^\circ\). In this experiment the angle is measured between the incident and scattered beams of electrons. The presence of this peak at 50\(^\circ\) is taken as evidence of constructive interference of the de Broglie waves demonstrating that the electrons are diffracted by the Nickel target and that they have wave properties that govern their propagation.

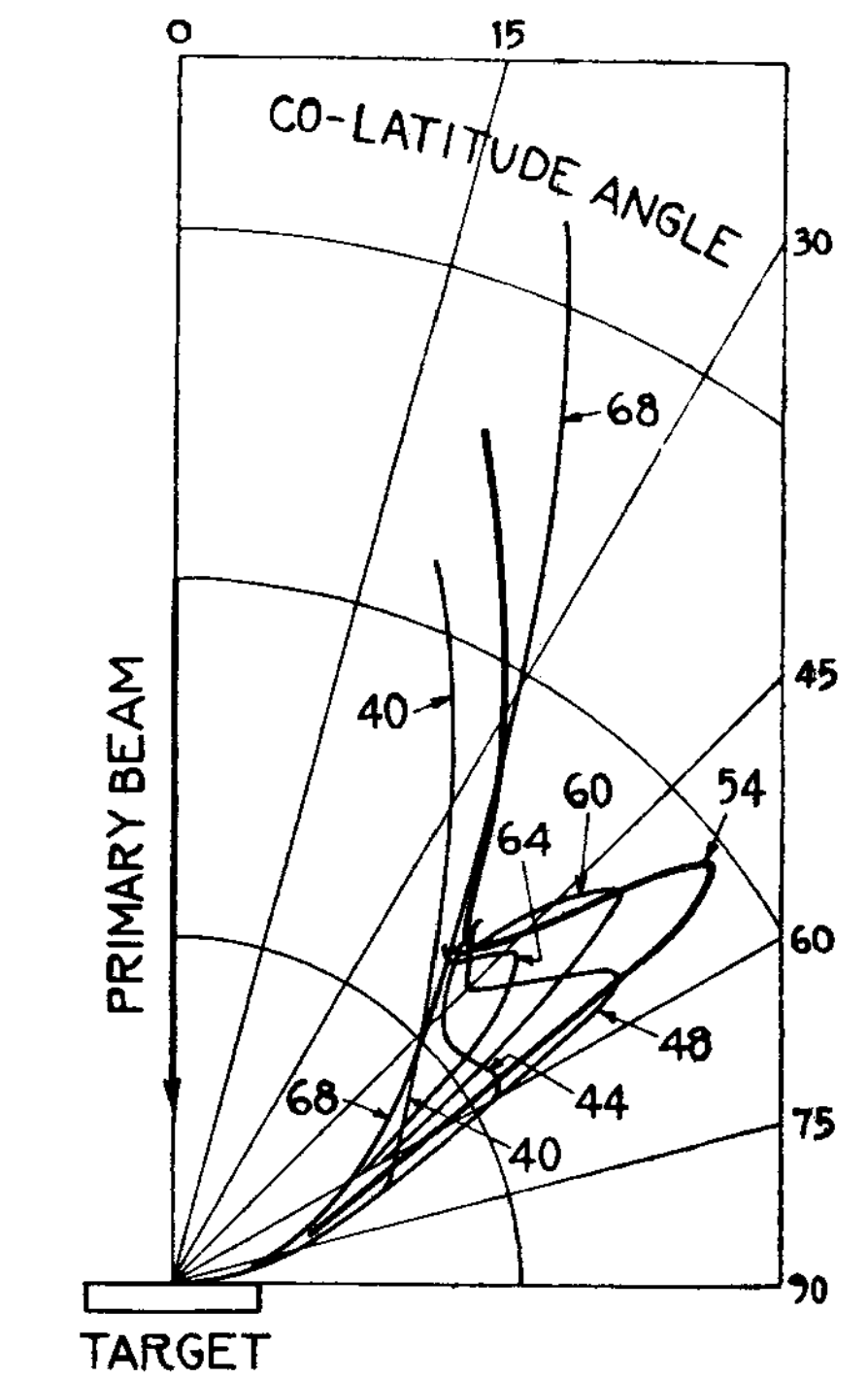
Fig. 1.14 The experimental data obtained by Davisson and Germer (DavissonGermer1927). You can clearly see that the current in the detector is a maximum for an accelerating voltage of 54 V when the detector is placed and an angle of 50\(^\circ\). Other accelerating voltages show the angle of the maximum changes with the accelerating voltage.

The electrons wave like behaviour obeys the Bragg formula for diffraction.

\[ n\lambda = 2d \sin(\theta_\text{B}) \]

where n is the number of the maxima, \(\lambda\) will be the de Broglie wavelength in this case, \(d\) is the separation between the planes of atoms in the crystal, and \(\theta_\text{B}\) is the scattering angle. This is shown in figure 1.15 note that the angle for Bragg diffraction and the angle for the scattered electrons are not the same. The experimentally obtained scattering angle \(\theta_\text{S}\) is related to \(\theta_\text{B}\) by \(\theta_\text{S} = 90^\circ-\frac{50^\circ}{2}=65^\circ\), which is clearly labelled in the diagram.

X-ray diffraction performed on Nickel shows that \(d=0.91\times10^{-10}\)m. Substituting this into the Bragg formula gives \(\lambda=1.65\times10^{-10}\)m. As we saw in the example above, this is sufficiently close to the de Broglie wavelength of electrons accelerated to a kinetic energy of 54 eV that we can consider this experiment is proof of wave like behaviour of particles.

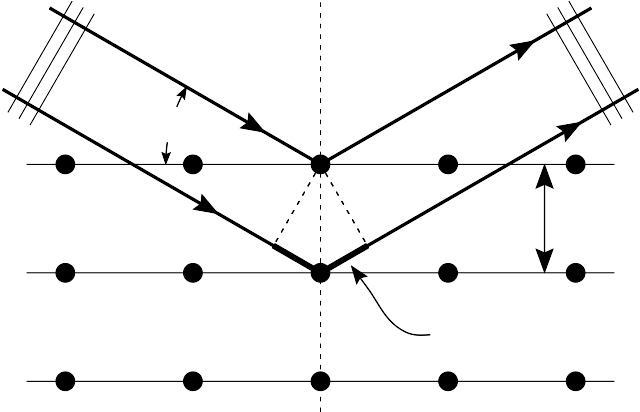
Fig. 1.15 A schematic representation of Bragg diffraction from the different planes of atoms in the crystalline target.

This experiment was initially performed with electron due to the relative ease of production. Davisson and Germer were not initially looking to prove the de Broglie hypothesis but to study the surface of nickel. Diffraction of other particles is also possible. Today neutron diffraction is employed as a non-invasive method for studying rare materials, see for example the work performed using the ISIS neutron source to investigate artifacts from ancient Egypt.

1.5.3. References

(DavissonGermer1927) Davisson, C., Germer, L.H. The Scattering of Electrons by a Single Crystal of Nickel. Nature 119, 558–560 (1927). https://doi.org/10.1038/119558a0