1.7. The Bohr model#

1.7.1. Introduction#

The Bohr model was an early attempt to explain the electron shell structure observed in atoms. In order to fit the observed evidence Bohr postulated that

  • electrons are confined to circular orbits around a nucleus and we will only consider 1 electron orbiting the nucleus,

  • the nucleus can posses any number of protons and neutrons,

  • electrons have an angular momentum \(L\) that is an integer number of \(\hbar\).

  • an accelerating electron does not radiate energy due to its circular path.

  • an electromagnetic wave will be emitted when an electron changes orbitals.

1.7.2. Bohr orbitals#

We will use Bohr’s postulates to determine the allowed energy for electron orbits. By equating the electrostatic force between the electron and the nucleus to the centripetal force due to the circular orbit we get

(1.17)#\[ k\frac{Ze^2}{r^2}=\mu\frac{v^2}{r} \text{ where } k=\frac{1}{4\pi\epsilon_0} \]

Where \(Z\) is the proton number, \(e\) is the electron charge, \(v\) is the electrons velocity and \(r\) is the orbital radius. Note: we have used the reduced mass so that

\[ \mu=\frac{m_e m_n}{m_e+m_n} \]

where \(m_e\) is the mass of the electron and \(m_n\) is the mass of the atomic nucleus. In the case where \(m_e<<m_n\) then \(\mu\approx m_e\) and we can replace \(\mu\) with \(m_e\). I will leave this as an exercise for you to demonstrate this approximation works.

Treating the electrons as de Broglie waves we can say that the circumference of an electrons orbit must be an integer number of de Broglie wavelengths, this is called a periodic boundary condition. The periodic boundary condition ensures that the de Brolgie waves are continuous around the orbit as shown in the animation below.

../_images/bohrorbits.gif

Fig. 1.19 An animation of a de Broglie wave superimposed over a Bohr orbit.#

1.7.3. Quantisation of angular momentum#

The periodic boundary condition can be expressed mathematically as

\[\begin{split} 2\pi r &= n\lambda,\\ &= n\frac{h}{p} \text{ where n=1,2,3,...}. \end{split}\]

Rearranging and substituting \(p=mv\) it is found that angular momentum is quantised.

(1.18)#\[ mvr = L = n\hbar. \]

Where \(L\) is the angular momentum and \(\lambda\) is the de Broglie wavelength and we call \(n\) the principle quantum number.

For the above animation, what is the value of the principle quantum number n?

There are 4 complete de Broglie waves in the orbit. That make the principle quantum number \(n=4\)

1.7.4. Energy of bohr orbitals#

From equation (1.18) we can see that the requirement for an integer number of de Broglie wavelengths leads to the quantisation of angular momentum \(L\). We will now find an expression for the total energy of a particle in a particular orbit. By substituting equation (1.18) into equation (1.17) we can first eliminate \(v\) and obtain and expression for \(r\).

(1.19)#\[ r=\frac{1}{k}\frac{n^2\hbar^2}{\mu Ze^2}. \]

Next eliminate \(r\) and obtain an expression for \(v\).

(1.20)#\[ v=\frac{n\hbar}{\mu r}=k\frac{Ze^2}{n\hbar}. \]

Equations (1.19) and (1.20) are called the Bohr radius and Bohr velocity, respectively. They will be required in the next step to simplify the expression for the total energy of the orbital electrons. Let’s now calculate the energy levels (total energy) for Bohr orbits by taking the sum of the potential energy \(V\) and kinetic energy \(E_k\).

(1.21)#\[\begin{split} E&=V+E_k,\\ &=-k\frac{Ze^2}{r}+\frac{1}{2}\mu v^2,\\ &=-k\frac{Ze^2}{r}+k\frac{Ze^2}{2r} \\ &=-\frac{\mu Z^2 e^4}{(4\pi\epsilon_0)^2 2\hbar^2}\frac{1}{n^2} \text{ where } n=1,2,3,4,... \end{split}\]

Hence, the quantisation of angular momentum leads to the quantisation of the total energy. Note the expression for kinetic energy used above is most easily found be rearranging equation (1.17). Now substitute the constants into equation (1.21) and convert the value into eV and the equation becomes

\[ E_n=-13.6\frac{Z^2}{n^2} \]

The first 5 Bohr energies for hydrogen are tabulated below

##print the first 5 bohr energies

##pass the Z and n, returns the bohr energy
def En(Z,n):
    return -1*(Z**2)*13.6/n**2

#ground state energy for atomic hydrogen
E1 = -13.6 #eV

##print the Bohr energies
print("The energies of the first 5 Bohr orbitals are: ")

for i in range(1,5):
    print("n= ", i, "\t E", i ,"= ", format(En(1,i),'.2f'), "eV")
    

The energies of the first 5 Bohr orbitals are: 
n=  1 	 E 1 =  -13.60 eV
n=  2 	 E 2 =  -3.40 eV
n=  3 	 E 3 =  -1.51 eV
n=  4 	 E 4 =  -0.85 eV

The Bohr model fails to predict many states for atoms with a larger \(Z\) than hydrogen. However, it does predict the energy levels of hydrogen like ions, i.e. those ions of higher \(Z\) atoms with only one orbital electron (e.g, He\(_{1+}\), Li\(_{2+}\).) Below is a comparison of Hydrogen and Helium 1+ (i.e. Hydrogen like) as calculated using the Bohr model.

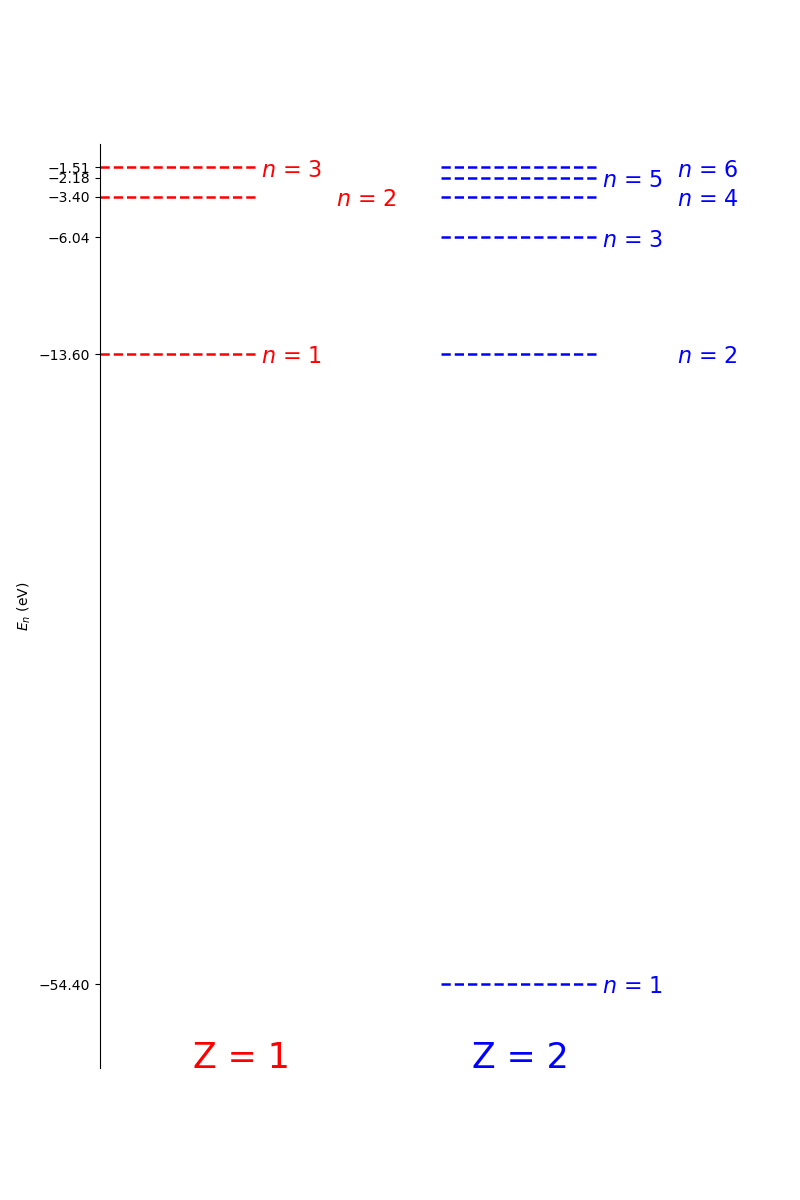
../_images/bohr-orbit-comparison.png

Fig. 1.20 A comparison of the first 3 and 6 Bohr orbits for hydrogen-like nuclei with \(Z=1\) and \(Z=2\), respectively. Note that Bohr states in Hydrogen correspond to the n=2, 4, 6, and higher, states in Helium 1+. The ground state (n=1) is much lower in energy in Helium that in Hydrogen. This is due to the additional binding energy provided by the extra proton in the Helium nucleus.#