BIOLOGICAL FLUID DYNAMICS OF SWIMMING MICROORGANISMS (theory & experiments)

1. M. A. Bees. Non-linear pattern generation by swimming micro-organisms. PhD thesis, University of Leeds, 1996.

2. M. A. Bees and N. A. Hill. Wavelengths of bioconvection patterns. Journal of Experimental Biology, 200(10):1515-1526, 1997.

3. M. A. Bees and N. A. Hill. Linear bioconvection in a suspension of randomly swimming, gyrotactic micro-organisms. Physics of Fluids, 10(8):1864-1881 (August) 1998.

4. M. A. Bees, N. A. Hill and T. J. Pedley. Analytical approximations for the orientation distribution of small dipolar particles in steady shear flows. Journal of Mathematical Biology, 36:269-298, 1998.

5. M. A. Bees and N. A. Hill. Non-linear bioconvection in a deep suspension of gyrotactic swimming micro-organisms. Journal of Mathematical Biology, 38(2):135-168, 1999.

6. M. A. Bees, P. Andresén, E. Mosekilde and M. Giskov. The interaction of thin-film flow, bacterial swarming and cell differentiation in colonies of Serratia liquefaciens. Journal of Mathematical Biology 40(1):27-63, 2000.

7. M. A. Bees, P. Andresén, E. Mosekilde and M. Givskov. Quantitative effects of medium hardness and nutrient availability on the swarming motility of Serratia liquefaciens. Bulletin of Mathematical Biology, 64(3):565-587, 2002.

8. N. A. Hill and M. A. Bees. Taylor dispersion of gyrotactic swimming micro-organisms in a linear flow. Physics of Fluids, 14(8):2598-2605, 2002.

9. N. A. Hill and M. A. Bees. Physics of Fluids article also available in the Virtual Journal of Biological Physics Research, 3(12), 2002.

10. Luis H. Cisneros, Ricardo Ortiz, Ricardo Cortez, John O. Kessler and Martin A. Bees. Unexpected bipolar flagellar arrangements and long-range flows driven by bacteria near solid boundaries. Physical Review Letters 101(16):168102-1, 2008.

11. M. A. Bees and O. A. Croze. Dispersion of biased swimming microorganisms in a fluid flowing through a tube. Proceedings of the Royal Society A, doi:10.1098/rspa.2009.0606, 2010.

12. O. A. Croze, E. E. Ashraf and M. A. Bees. Sheared bioconvection in a horizontal tube. Physical Biology, 7(4), doi:10.1088/1478-3975/7/4/046001, 2010.

13. O. A. Croze, E. E. Ashraf and M. A. Bees. Patterns of swimming algae in horizontal pipe flow, Physical Biology Labtalk feature. Jan 26th, 2011.

14. C. R. Williams and M. A. Bees. Photo-gyrotactic bioconvection. Journal of Fluid Mechanics, doi:10.1017/jfm.2011.100, 1-46, 2011.

15. C. R. Williams and M. A. Bees. A tale of three taxes: photo-gyro-gravitactic bioconvection. Journal of Experimental Biology 214:2398-2408, 2011.

    Link to Inside JEB article: Journal of Experimental Biology, June 2011, Published by The Company of Biologists Ltd.

    Link to Nature Research Highlights article: Nature, 474:544, 30th June 2011.

16. S. O. Malley and M. A. Bees. The orientation of swimming bi-flagellates in shear flows. Bulletin of Mathematical Biology doi:10.1007/s11538-011-9673-1, 74:232–255, 2012.

17. Vincent A. Martinez, Rut Besseling, Ottavio A. Croze, Julien Tailleur, Mathias Reufer, Jana Schwarz-Linek, Laurence G. Wilson, Martin A. Bees and Wilson C. K. Poon. Differential Dynamic Microscopy: a High-Throughput Method for Characterizing the Motility of Microorganisms. Biophysical Journal 103:1637-1647, 2012.

18. R. N. Bearon, M. A. Bees and O. A. Croze. Biased swimming cells do not disperse in pipes as tracers: a population model based on microscale behaviour. Physics of Fluids 24:121902, 2012.

19. Ottavio A. Croze, Gaetano Sardina, Mansoor Ahmed, Martin A. Bees and Luca Brandt. Dispersion of swimming algae in laminar and turbulent channel flows: theory and simulations. Journal of the Royal Society Interface 10:20121041, 14 pages, 2013.

20. O. A. Croze, R. N. Bearon and M. A. Bees. Taylor-Aris dispersion of swimming algae in pipe flow: experimental test of competing theories. 2013.

21. C. R. Williams and M. A. Bees. Mechanistic modelling of sulfur-deprived photosynthesis and hydrogen production in suspensions of Chlamydomonas reinhardtii. Biotechnology and Bioengineering 111(2):320-335 2014.

22. M. A. Bees and O.A. Croze. Mathematics for streamlined biofuel production from unicellular algae. Biofuels 5(1):53-65 2014.

23. D. O. Pushkin and M. A. Bees. Bugs on a slippery plane: Understanding the motility of microbial pathogens with mathematical modelling. Biophysics of Infection, Advances in Experimental Medicine and Biology, M.C. Leake (ed.), 915:193-205 (DOI 10.1007/978-3-32189-9 12) 2016.

24. A. Hope, O. A. Croze, W. C. K. Poon, M. A. Bees and M. D. Haw. Resonant alignment of microswimmer trajectories in oscillatory shear flows. Physical Review Fluids 1:051201 2016.

25. L. N. Alsharief, M. A. Bees and J. W. Pitchford. Bioconvection as a mechanism to promote biodiversity. Submitted to Theoretical Ecology 2016.

26. O. A. Croze, R. N. Bearon and M. A. Bees. Gyrotactic swimmer dispersion in pipe flow: testing the theory. Journal of Fluid Mechanics 816:481-506 2017.

27. C. Alfiniyah, M. A. Bees and A. J. Wood. Pulse generation in the quorum machinery of Pseudomonas aeruginosa. Journal of Mathematical Biology DOI 10.1007/s11538-017-0288-z 2017.

28. N.E. Farthing, R.C. Findlay, K.F. Jikeli, P.B. Walrad, M.A. Bees, and L.G. Wilson. Simultaneous two-color imaging in digital holographic microscopy. Optics Express 25:28489-28500 2017.

29. F. J. Peaudecerf, F. Bunbury, V. Bhardwaj, M. A. Bees, A. G. Smith, R. E. Goldstein and O. A. Croze. Microbial mutualism at a distance: The role of geometry in diffusive exchanges. Physical Review E 97:022411 2018.

30. Ottavio A. Croze, Vincent A. Martinez, Theresa Jakuszeit, Dario Dell’Arciprete, Wilson C. K. Poon and Martin A. Bees. Helical and oscillatory microswimmer motility statistics from differential dynamic microscopy. New Journal of Physics 21:063012 2019.

T. B. Rasmussen, T. T. Nielsen, L. Eberl, M. A. Bees, S. Molin and M. Givskov. Surface conditioning in a swarming colony: cells have different assignments. In prep. 2008.

M. A. Bees. Similarity solutions for a lubrication model of bacterial swarming. In prep. 2008.

31. M. A. Bees, I. Mezic and J. McGlade. Planktonic interactions and chaotic advection in Langmuir circulation. IMACS Mathematics and Computers in Simulation, 44(6):527-544, 1998.

32. M. A. Bees. Planktonic communities and chaotic advection in dynamic models of Langmuir circulation. Applied Scientific Research, 59:141-158, 1998.

33. A. M. Edwards and M. A. Bees. Generic dynamics of a simple plankton model with a non-integer exponent of closure. Chaos, Solitons and Fractals (special refereed edition on Chaos in Ecology), 12(2):289-300, 2001. 

34. R. Reigada, R. Hillary, M. A. Bees, J. M. Sancho and F. Sagués. Plankton blooms induced by turbulent flows.  Proceedings of the Royal Society B, 270:875-880, 2003.

35. F. Sagués, R. Reigada, J. M. Sancho, R. M. Hillary, and M. A. Bees.  Synthesizing Hydrodynamic Turbulence from Noise: Formalism and Applications to Plankton Dynamics.  In Unsolved problems of Noise and Fluctuations; Bezrukov, S. M. (edt.)  AIP Proc. 665, 531 (2003)

36. R. M. Hillary and M. A. Bees. Plankton lattices and the role of chaos in plankton patchiness. Physical Review E 69:031913, 2004.

37. R. M. Hillary and M. A. Bees. PRE article also available in the Virtual Journal of Biological Physics Research, 7(7), 2004.

38. R. M. Hillary and M. A. Bees. Synchrony and chaos in patchy ecosystems. Bulletin of Mathematical Biology 66(6):1909-1931, 2004. 

39. E. J. Guirey, M. A. Bees, A. P. Martin, M. A. Srokosz and M. J. R. Fasham. Emergent features due to grid-cell biology: synchronisation in biophysical models. Bulletin of Mathematical Biology DOI:10.1007/s11538-006-9180-y, 2007. 

40. E. J. Guirey, A. P. Martin, M. A. Srokosz and M. A. Bees. The Prairie Ocean. Extreme Events: Proc. 15th ‘Aha Huliko ‘a Hawaiian Winter Workshop, Honolulu, HI, US Office of Naval Research, the School of Ocean and Earth Science and Technology, and the Department of Oceanography, University of Hawaii at Manoa, 2007. 

41. E. J. Guirey, A. P. Martin, M. A. Srokosz and M. A. Bees,. Cluster synchronisation: a mechanism for plankton patchiness and a simulation pitfall. Ocean Modelling 29(4):223-233. 2009. 

42. E. J. Guirey, M. A. Bees,, A. P. Martin and M. A. Srokosz. Persistence of cluster synchronisation under the influence of advection. Physical Review E 81(5) DOI: 10.1103/PhysRevE.81.051902, 2010. 

43. W. Clifton, R. N. Bearon and M. A. Bees. Enhanced sedimentation of elongated plankton in simple flows. IMA Journal of Applied Mathematics 83:743–766 doi:10.1093/imamat/hxy024, 2018. 

44. J. R. Woodward, J. W. Pitchford and M. A. Bees. Physical Flow Effects Can Dictate Plankton Population Dynamics. Journal of the Royal Society Interface 16:20190247 doi.org/10.1098/rsif.2019.0247, 2019. 

M. A. Bees and A. M. Edwards. Bioconvection driven by planktonic light absorption in oceans and lakes. In prep., 2008.

CHEMICAL SYSTEMS & CHEMOCONVECTION (theory & experiments)

45. A. J. Pons, P. G. Sørensen, M. A. Bees and F. Sagués. Pattern formation in the Methylene-Blue Glucose system. Journal of Physical Chemistry, 104B:2251-2259, 2000.

46. M. A. Bees, A. J. Pons, P. G. Sørensen and F. Sagués. "Chemoconvection": a chemically driven hydrodynamic instability. Journal of Chemical Physics 114(4):1-12, 2001.

47. A. J. Pons, F. Sagués, M. A. Bees and P. G. Sørensen. Quantitative analysis of chemoconvection patterns in the Methylene-Blue-Glucose system.  Journal of Physical Chemistry, 106B:7252-7259, 2002.

48. A. J. Pons, F. Sagués and M. A. Bees. Chemoconvection patterns in the methylene-blue-glucose system: weakly non-linear analysis. Physical Review E 70:066304, 2004.

49. A. J. Pons, O. Batiste and M. A. Bees. Nonlinear chemoconvection in the Methylene-Blue--Glucose system: 2D shallow layers. Physical Review E 78:016316, 2008.

ECOLOGY & BIOCONTROL

50. M. A. Bees. A mathematical model of speciation. In Bio-physical Models of Oceanic Population Dynamics; 1994 Summer Study Program in Geophysical Fluid Dynamics. Woods Hole Oceanog. Inst. Tech. Rept., WHOI-97-18 (1997). Woods Hole Oceanographic Institution, Woods Hole, Massachusetts 02543, U.S.A.

51. D. Schley and M. A. Bees. A discrete slug population model determined by egg production. Journal of Biological Systems 10(3):243-264, 2002.

52. D. Schley and M. A. Bees. Delay dynamics of the slug Deroceras reticulatum, an agricultural pest. Ecological Modelling 162:177-198, 2003.

53. Media articles (2000/2001) on “Mathematical modelling of beetle-nematode slug-biocontrol”: approx. 15 articles in a wide range of newspapers, magazines, brochures, websites (such as EPSRC), radio and TV, with which I had either some input or ultimate editorial control. For example, see Daily Mail Apr 17th, 2000, pg. 35; Organic Living, Harrogate, Yorks, Jun 2001; EPSRC “Mathematics Underpinning the Life Sciences” programme advertisement, 2001.

54. D. Schley and M. A. Bees.  The role of time delays in a non-autonomous host-parasitoid model of slug biocontrol with nematodes.  Ecological Modelling 193:543-559, 2006.

55. M. A. Bees, O. Angulo, J. C. Lopez-Marcos and D. Schley. Dynamics of a structured slug population model in the absence of seasonal variation. Mathematical Models & Methods in Applied Sciences 12(16):1961-1985, 2006.

56. M. A. Bees, P. H. Coullet and E. A. Spiegel. On the bifurcation of species. CHAOS 18,043114:1-12, 2008.

57. M. A. Bees, P. H. Coullet and E. A. Spiegel. CHAOS article also available in the Virtual Journal of Biological Physics Research, 16(10), 2008.

58. O. Angulo, J. C. Lopez-Marcos and M. A. Bees. Mass structured systems with boundary delay: oscillations and the effect of selective predation. Journal of Nonlinear Science, DOI 10.1007/s00332-012-9133-6, 2012.

D. Schley and M. A. Bees. The self-restrained slug. In prep., 2006.

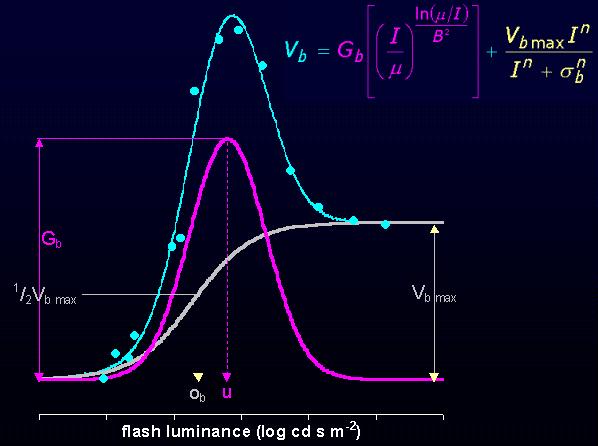
PHYSIOLOGY (theory & experiments)

59. R. Hamilton, M. A. Bees, C. A. Chaplin and D. L. McCulloch.  The luminance-response function of the human photopic electroretinogram: a mathematical model.  Vision Research 47:2968-2972, 2007.

60. M.-L. Garon, R. Hamilton, D. L. McCulloch, M. A. Bees, J. M. Little, R. C. Polomeno, R. K. Koenekoop and P. Lachapelle  Analysis of the photopic hill: testing the Glasgow model.  Investigative Ophthalmology & Visual Science 48(13):529, 2007.